Đề bài
Biểu đồ dưới đây biểu diễn mẫu số liệu ghép nhóm mức lương nhân viên một công ty (đơn vị: triệu đồng).
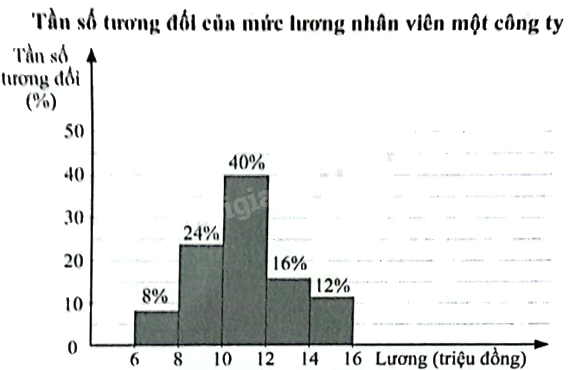
Biết công ty có 25 nhân viên.
Sử dụng biểu đồ trên, viết số thích hợp vào chỗ chấm trong các câu sau:
a) Tần số của nhóm \(\left[ {6;8} \right)\) là ………
b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là ……… triệu đồng.
c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là \(\frac{a}{{12}}\) với \(a\) bằng ………
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là \(\frac{b}{{24}}\) với \(b\) bằng ………
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
Tứ phân vị thứ \(k\) được xác định như sau: \({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}\left( {{u_{m + 1}} - {u_m}} \right)\)
trong đó:
• \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu;
• \(\left[ {{u_m};{u_{m + 1}}} \right)\) là nhóm chứa tứ phân vị thứ \(k\);
• \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ \(k\);
• \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1}\).
Lời giải chi tiết
Ta có bảng tần số ghép nhóm như sau:
Vậy tần số của nhóm \(\left[ {6;8} \right)\) là 8%.
Khoảng biến thiên của mẫu số liệu trên là: \(R = 16 - 6 = 10\) (triệu đồng).
Gọi \({x_1};{x_2};...;{x_{100}}\) là mẫu số liệu gốc.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{26}} \in \left[ {8;10} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 8 + \frac{{\frac{{1.100}}{4} - 8}}{{24}}\left( {10 - 8} \right) = \frac{{113}}{{12}}\).
Vậy \(a = 113\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{76}} \in \left[ {12;14} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 12 + \frac{{\frac{{3.100}}{4} - \left( {8 + 24 + 40} \right)}}{{16}}\left( {14 - 12} \right) = \frac{{99}}{8}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\(\Delta Q = {Q_3} - {Q_1} = \frac{{99}}{8} - \frac{{113}}{{12}} = \frac{{71}}{{24}}\) (triệu đồng). Vậy \(b = 71\).
a) 2.
b) 10.
c) 113.
d) 71.
