Giải bài 6 trang 34 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 6 trang 34 SBT Toán 12 Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết bài 6 trang 34 sách bài tập Toán 12 Chân trời sáng tạo. Tusach.vn cung cấp đáp án chính xác, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập Toán 12.
Chúng tôi luôn cập nhật nhanh chóng và đầy đủ lời giải của tất cả các bài tập trong sách bài tập Toán 12 Chân trời sáng tạo.
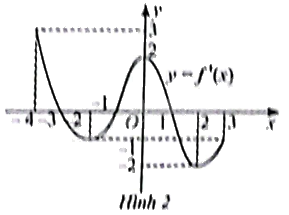
Đồ thị đạo hàm \(f'\left( x \right)\) của hàm số \(y = f\left( x \right)\) được cho trong Hình 2. Điểm cực tiểu của hàm số \(y = f\left( x \right)\) là A. \(x = - 3\). B. \(x = - 1\). C. \(x = 0\). D. \(x = 1\).
Đề bài
Đồ thị đạo hàm \(f'\left( x \right)\) của hàm số \(y = f\left( x \right)\) được cho trong Hình 2.
Điểm cực tiểu của hàm số \(y = f\left( x \right)\) là
A. \(x = - 3\).
B. \(x = - 1\).
C. \(x = 0\).
D. \(x = 1\).
Phương pháp giải - Xem chi tiết
Từ đồ thị hàm số \(y = f'\left( x \right)\), lập bảng biến thiên của hàm số \(y = f\left( x \right)\) rồi xác định cực trị của hàm số.
Lời giải chi tiết
Ta có: \(y' = 0\) khi \(x = - 1;x = 1\) hoặc \(x = - 2\).
Bảng xét dấu đạo hàm của hàm số:

Dựa vào bảng xét dấu đạo hàm ta có: Hàm số đạt cực tiểu tại \(x = - 1\).
Chọn B.
Giải bài 6 trang 34 SBT Toán 12 Chân trời sáng tạo: Tổng quan và Phương pháp giải
Bài 6 trang 34 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản, kết hợp với các kỹ năng biến đổi đại số để tìm ra đáp án chính xác.
Nội dung chi tiết bài 6 trang 34 SBT Toán 12 Chân trời sáng tạo
Bài 6 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của các hàm số đơn thức, đa thức, hàm hợp, hàm lượng giác, hàm mũ, hàm logarit.
- Tìm đạo hàm cấp hai: Yêu cầu tính đạo hàm cấp hai của một hàm số cho trước.
- Ứng dụng đạo hàm để giải phương trình: Sử dụng đạo hàm để tìm cực trị, điểm uốn của hàm số, hoặc giải các phương trình liên quan đến đạo hàm.
- Bài toán thực tế: Một số bài tập có thể liên hệ với các bài toán thực tế, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết.
Lời giải chi tiết bài 6 trang 34 SBT Toán 12 Chân trời sáng tạo
Dưới đây là lời giải chi tiết cho từng phần của bài 6 trang 34 SBT Toán 12 Chân trời sáng tạo:
Ví dụ 1: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1
Lời giải:
f'(x) = 3x2 + 4x - 5
Ví dụ 2: Tìm đạo hàm cấp hai của hàm số g(x) = sin(x)
Lời giải:
g'(x) = cos(x)
g''(x) = -sin(x)
Phương pháp giải bài tập đạo hàm hiệu quả
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:
- Nắm vững các quy tắc tính đạo hàm: Đạo hàm của hàm số đơn thức, đa thức, hàm hợp, hàm lượng giác, hàm mũ, hàm logarit.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi có chức năng tính đạo hàm, hoặc các phần mềm giải toán trực tuyến.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tại sao nên chọn tusach.vn để giải bài tập Toán 12?
Tusach.vn là địa chỉ tin cậy cho học sinh, sinh viên và giáo viên cần tìm kiếm lời giải bài tập Toán 12. Chúng tôi cung cấp:
- Lời giải chi tiết, dễ hiểu: Được trình bày rõ ràng, logic, giúp bạn nắm vững kiến thức.
- Cập nhật nhanh chóng: Luôn cập nhật lời giải của các bài tập mới nhất.
- Đội ngũ chuyên gia giàu kinh nghiệm: Đảm bảo tính chính xác và chất lượng của lời giải.
- Giao diện thân thiện, dễ sử dụng: Giúp bạn tìm kiếm thông tin một cách nhanh chóng và thuận tiện.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chương | Bài | Nội dung |
|---|---|---|
| 1 | 6 | Đạo hàm |