Đề bài
Người ta muốn dựng một cột ăng-ten trên một sườn đồi. Ăng-ten được dựng thẳng đứng trong không gian \(Oxyz\) với độ dài đơn vị trên mỗi trục bằng 1 m. Gọi \(O\) là gốc cột, \(A\) là điểm buộc dây cáp vào cột ăng-ten và \(M,N\) là hai điểm neo dây cáp xuống mặt sườn đồi (Hình 6). Cho biết toạ độ các điểm nói trên lần lượt là \(O\left( {0;0;0} \right),A\left( {0;0;6} \right),M\left( {3; - 4;3} \right),\)\(N\left( { - 5; - 2;2} \right)\).
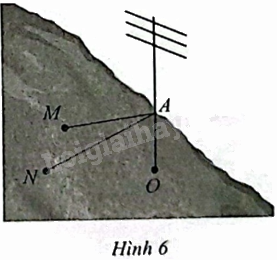
a) Tính độ dài các đoạn dây cáp \(MA\) và \(NA\).
b) Tính góc tạo bởi các sợi dây cáp \(MA,NA\) với mặt phẳng sườn đồi.
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính độ dài đoạn thẳng \(AB\):
\(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \).
‒ Đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( {{a_1};{b_1};{c_1}} \right)\) và mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến \(\overrightarrow n = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó ta có:
\(\sin \left( {\Delta ,\left( P \right)} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right| = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\).
Lời giải chi tiết
a) Ta có: \(MA = \left| {\overrightarrow {MA} } \right| = \sqrt {{{\left( {0 - 4} \right)}^2} + {{\left( {0 - \left( { - 4} \right)} \right)}^2} + {{\left( {6 - 3} \right)}^2}} = \sqrt {34} \approx 5,8\left( m \right)\).
\(NA = \left| {\overrightarrow {NA} } \right| = \sqrt {{{\left( {0 - \left( { - 5} \right)} \right)}^2} + {{\left( {0 - \left( { - 2} \right)} \right)}^2} + {{\left( {6 - 2} \right)}^2}} = \sqrt {45} \approx 6,7\left( m \right)\).
b) Ta có: \(\overrightarrow {MA} = \left( { - 3;4;3} \right),\overrightarrow {NA} = \left( {5;2;4} \right),\overrightarrow {OM} = \left( {3; - 4;3} \right),\overrightarrow {ON} = \left( { - 5; - 2;2} \right)\)
\(\left[ {\overrightarrow {OM} ,\overrightarrow {ON} } \right] = \left( { - 2; - 21; - 26} \right)\).
Do đó \(\left( {OMN} \right)\) có vectơ pháp tuyến \(\overrightarrow n = \left( { - 2; - 21; - 26} \right)\).
Ta có:
\(\sin \left( {MA,\left( {OMN} \right)} \right) = \left| {\cos \left( {\overrightarrow {MA} ,\overrightarrow n } \right)} \right| = \frac{{\left| {\left( { - 3} \right).\left( { - 2} \right) + 4.\left( { - 21} \right) + 3.\left( { - 26} \right)} \right|}}{{\sqrt {{{\left( { - 3} \right)}^2} + {4^2} + {3^2}} .\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 21} \right)}^2} + {{\left( { - 26} \right)}^2}} }} = \frac{{156}}{{\sqrt {38114} }}\)
Vậy \(\left( {MA,\left( {OMN} \right)} \right) \approx {53^ \circ }\).
\(\sin \left( {NA,\left( {OMN} \right)} \right) = \left| {\cos \left( {\overrightarrow {NA} ,\overrightarrow n } \right)} \right| = \frac{{\left| {5.\left( { - 2} \right) + 2.\left( { - 21} \right) + 4.\left( { - 26} \right)} \right|}}{{\sqrt {{5^2} + {2^2} + {4^2}} .\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 21} \right)}^2} + {{\left( { - 26} \right)}^2}} }} = \frac{{156}}{{\sqrt {50445} }}\)
Vậy \(\left( {NA,\left( {OMN} \right)} \right) \approx {44^ \circ }\).
