Giải bài 5 trang 33 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 5 trang 33 Sách bài tập Toán 12 - Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết bài 5 trang 33 Sách bài tập Toán 12 Chân trời sáng tạo. Tại tusach.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập Toán 12.
Bài viết này sẽ hướng dẫn bạn từng bước giải bài tập, đồng thời cung cấp các kiến thức nền tảng cần thiết.
Cho hàm số \(y = {x^3} + 4{x^2} - 3x + 4\). Khi đó A. Hàm số đạt cực đại tại \(x = \frac{1}{3}\), giá trị cực đại là \(\frac{{94}}{{27}}\). B. Hàm số đạt cực đại tại \(x = - 3\), giá trị cực đại là 22. C. Hàm số đạt cực đại tại \(x = 0\), giá trị cực đại là 4. D. Hàm số không có cực đại.
Đề bài
Cho hàm số \(y = {x^3} + 4{x^2} - 3x + 4\). Khi đó
A. Hàm số đạt cực đại tại \(x = \frac{1}{3}\), giá trị cực đại là \(\frac{{94}}{{27}}\).
B. Hàm số đạt cực đại tại \(x = - 3\), giá trị cực đại là 22.
C. Hàm số đạt cực đại tại \(x = 0\), giá trị cực đại là 4.
D. Hàm số không có cực đại.
Phương pháp giải - Xem chi tiết
Các bước để tìm cực trị của hàm số \(f\left( x \right)\):
Bước 1. Tìm tập xác định \(D\) của hàm số.
Bước 2. Tính đạo hàm \(f'\left( x \right)\) của hàm số. Tìm các điểm \({x_1},{x_2},...,{x_n} \in D\) mà tại đó đạo hàm \(f'\left( x \right)\) bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm \({x_1},{x_2},...,{x_n}\) theo thứ tự tăng dần, xét dấu \(f'\left( x \right)\) và lập bảng biến thiên.
Bước 4. Nêu kết luận về cực trị của hàm số.
Lời giải chi tiết
Xét hàm số \(y = {x^3} + 4{x^2} - 3x + 4\).
Tập xác định: \(D = \mathbb{R}\).
Ta có \(y' = 3{x^2} + 8x - 3;y' = 0 \Leftrightarrow x = \frac{1}{3}\) hoặc \(x = - 3\).
Bảng biến thiên:
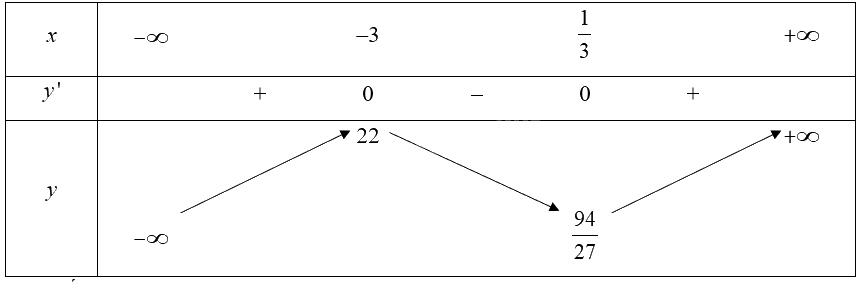
Hàm số đạt cực đại tại $x=-3,{{y}_{CĐ}}=22$.
Chọn B.
Giải bài 5 trang 33 Sách bài tập Toán 12 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Bài 5 trang 33 Sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào chủ đề về Đạo hàm của hàm số hợp. Đây là một phần quan trọng trong chương trình, giúp học sinh hiểu rõ hơn về các quy tắc tính đạo hàm và ứng dụng chúng vào giải quyết các bài toán thực tế.
Nội dung chính của bài 5 trang 33
Bài 5 yêu cầu học sinh vận dụng các quy tắc đạo hàm đã học để tính đạo hàm của các hàm số hợp. Các dạng bài tập thường gặp bao gồm:
- Tính đạo hàm của hàm số hợp đơn giản (ví dụ: y = u(v(x))).
- Tính đạo hàm của hàm số hợp phức tạp hơn, đòi hỏi phải áp dụng nhiều quy tắc đạo hàm.
- Tìm đạo hàm cấp hai của hàm số hợp.
- Ứng dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến, khoảng đơn điệu, cực trị của hàm số.
Lời giải chi tiết bài 5 trang 33 Sách bài tập Toán 12 - Chân trời sáng tạo
Để giúp các bạn học sinh hiểu rõ hơn về cách giải bài 5 trang 33, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi:
Câu a)
Đề bài: Tính đạo hàm của hàm số y = sin(x2 + 1)
Lời giải:
Đặt u = x2 + 1, khi đó y = sin(u). Áp dụng quy tắc đạo hàm của hàm số hợp, ta có:
y' = cos(u) * u' = cos(x2 + 1) * (2x) = 2x * cos(x2 + 1)
Câu b)
Đề bài: Tính đạo hàm của hàm số y = ecos(x)
Lời giải:
Đặt u = cos(x), khi đó y = eu. Áp dụng quy tắc đạo hàm của hàm số hợp, ta có:
y' = eu * u' = ecos(x) * (-sin(x)) = -sin(x) * ecos(x)
Mẹo giải bài tập về đạo hàm hàm số hợp
Để giải các bài tập về đạo hàm hàm số hợp một cách hiệu quả, bạn nên:
- Nắm vững các quy tắc đạo hàm cơ bản (đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit).
- Xác định đúng hàm số bên trong (u) và hàm số bên ngoài (v).
- Áp dụng quy tắc đạo hàm của hàm số hợp một cách chính xác: y' = v'(u) * u'.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Tài liệu tham khảo hữu ích
Ngoài sách bài tập Toán 12 Chân trời sáng tạo, bạn có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về đạo hàm:
- Sách giáo khoa Toán 12
- Các bài giảng trực tuyến về đạo hàm
- Các trang web học Toán uy tín
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các bạn học sinh sẽ tự tin giải bài 5 trang 33 Sách bài tập Toán 12 Chân trời sáng tạo và đạt kết quả tốt trong môn Toán. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ!
| Chủ đề | Nội dung |
|---|---|
| Quy tắc đạo hàm | Đạo hàm của hàm số hợp: y' = v'(u) * u' |
| Ví dụ minh họa | Giải chi tiết câu a, b bài 5 trang 33 |
| Mẹo giải | Nắm vững quy tắc, xác định hàm u, v chính xác |