Giải bài 10 trang 76 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 10 trang 76 sách bài tập Toán 12 Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết bài 10 trang 76 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
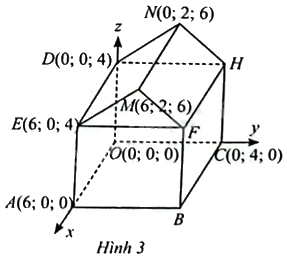
Một nhân viên đang sử dụng phần mềm để thiết kế khung của một ngôi nhà trong không gian (Oxyz) được minh hoạ như Hình 3. Cho biết (OABC.DEFH) là hình hộp chữ nhật và (EMF.DNH) là hình lăng trụ đứng. a) Tìm toạ độ của các điểm (B,F,H). b) Tìm toạ độ của các vectơ (overrightarrow {ME} ,overrightarrow {MF} ). c) Tính số đo (widehat {EMF}).
Đề bài
Một nhân viên đang sử dụng phần mềm để thiết kế khung của một ngôi nhà trong không gian \(Oxyz\) được minh hoạ như Hình 3. Cho biết \(OABC.DEFH\) là hình hộp chữ nhật và \(EMF.DNH\) là hình lăng trụ đứng.
a) Tìm toạ độ của các điểm \(B,F,H\).
b) Tìm toạ độ của các vectơ \(\overrightarrow {ME} ,\overrightarrow {MF} \).
c) Tính số đo \(\widehat {EMF}\).
Phương pháp giải - Xem chi tiết
‒ Sử dụng toạ độ của vectơ \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
‒ Sử dụng tính chất hai vectơ bằng nhau: Với \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\), ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\).
‒ Sử dụng công thức tính góc của hai vectơ \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\):
\(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{{x_1}.{x_2} + {y_1}.{y_2} + {z_1}.{z_2}}}{{\sqrt {x_1^2 + y_1^2 + z_1^2} .\sqrt {x_2^2 + y_2^2 + z_2^2} }}\).
Lời giải chi tiết
a) Giả sử \(B\left( {{x_B};{y_B};{z_B}} \right)\). Ta có
\(\overrightarrow {OA} = \left( {6;0;0} \right),\overrightarrow {CB} = \left( {{x_B};{y_B} - 4;{z_B}} \right)\).
\(OABC\) là hình chữ nhật nên \(\overrightarrow {OA} = \overrightarrow {CB} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 6\\{y_B} - 4 = 0\\{z_B} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 6\\{y_B} = 4\\{z_B} = 0\end{array} \right.\). Vậy \(B\left( {6;4;0} \right)\).
Giả sử \(F\left( {{x_F};{y_F};{z_F}} \right)\). Ta có
\(\overrightarrow {A{\rm{E}}} = \left( {0;0;4} \right),\overrightarrow {BF} = \left( {{x_F} - 6;{y_F} - 4;{z_F}} \right)\).
\(ABF{\rm{E}}\) là hình chữ nhật nên \(\overrightarrow {A{\rm{E}}} = \overrightarrow {BF} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_F} - 6 = 0\\{y_F} - 4 = 0\\{z_F} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 6\\{y_B} = 4\\{z_B} = 4\end{array} \right.\). Vậy \(F\left( {6;4;4} \right)\).
Giả sử \(H\left( {{x_H};{y_H};{z_H}} \right)\). Ta có
\(\overrightarrow {O{\rm{D}}} = \left( {0;0;4} \right),\overrightarrow {CH} = \left( {{x_H};{y_H} - 4;{z_H}} \right)\).
\(OCH{\rm{D}}\) là hình chữ nhật nên \(\overrightarrow {O{\rm{D}}} = \overrightarrow {CH} \).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_H} = 0\\{y_H} - 4 = 0\\{z_H} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_H} = 0\\{y_H} = 4\\{z_H} = 4\end{array} \right.\). Vậy \(H\left( {0;4;4} \right)\).
b) \(\overrightarrow {ME} = \left( {6 - 6;0 - 2;4 - 6} \right) = \left( {0; - 2; - 2} \right),\overrightarrow {MF} = \left( {6 - 6;4 - 2;4 - 6} \right) = \left( {0;2; - 2} \right)\).
c) \(\cos \widehat {EMF} = \cos \left( {\overrightarrow {ME} ,\overrightarrow {MF} } \right) = \frac{{0.0 + \left( { - 2} \right).2 + \left( { - 2} \right).\left( { - 2} \right)}}{{\sqrt {{0^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{0^2} + {2^2} + {{\left( { - 2} \right)}^2}} }} = 0\)
Vậy \(\widehat {EMF} = {90^ \circ }\).
Giải bài 10 trang 76 SBT Toán 12 Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 10 trang 76 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của hàm hợp và đạo hàm của hàm lượng giác. Việc nắm vững các công thức đạo hàm cơ bản và kỹ năng biến đổi đại số là yếu tố then chốt để giải quyết bài tập này một cách hiệu quả.
Nội dung chi tiết bài 10 trang 76 SBT Toán 12 Chân trời sáng tạo
Bài 10 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tính đạo hàm của hàm số lượng giác: Yêu cầu tính đạo hàm của các hàm số có chứa các hàm lượng giác như sin, cos, tan, cot.
- Dạng 2: Tính đạo hàm của hàm hợp: Yêu cầu tính đạo hàm của các hàm số được tạo thành từ việc hợp của nhiều hàm số khác nhau.
- Dạng 3: Tìm đạo hàm cấp hai: Yêu cầu tìm đạo hàm bậc hai của một hàm số.
- Dạng 4: Ứng dụng đạo hàm để giải các bài toán liên quan đến cực trị: Tìm cực đại, cực tiểu của hàm số.
Hướng dẫn giải chi tiết bài 10 trang 76 SBT Toán 12 Chân trời sáng tạo
Để giải bài 10 trang 76 SBT Toán 12 Chân trời sáng tạo một cách hiệu quả, các em cần thực hiện theo các bước sau:
- Xác định đúng công thức đạo hàm cần sử dụng: Dựa vào dạng hàm số, chọn công thức đạo hàm phù hợp.
- Thực hiện các phép biến đổi đại số: Đơn giản hóa biểu thức trước khi tính đạo hàm.
- Tính đạo hàm từng bước một: Tránh sai sót trong quá trình tính toán.
- Kiểm tra lại kết quả: Đảm bảo đáp án cuối cùng là chính xác.
Ví dụ minh họa giải bài 10 trang 76 SBT Toán 12 Chân trời sáng tạo
Ví dụ: Tính đạo hàm của hàm số y = sin(2x + 1).
Giải:
Sử dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x)
Đặt u(v) = sin(v) và v(x) = 2x + 1
Khi đó, u'(v) = cos(v) và v'(x) = 2
Vậy, y' = cos(2x + 1) * 2 = 2cos(2x + 1)
Lưu ý khi giải bài tập về đạo hàm
Để tránh mắc lỗi khi giải bài tập về đạo hàm, các em cần lưu ý những điều sau:
- Nắm vững các công thức đạo hàm cơ bản.
- Thực hành thường xuyên để làm quen với các dạng bài tập khác nhau.
- Kiểm tra lại kết quả sau khi tính toán.
- Sử dụng máy tính bỏ túi để kiểm tra lại đáp án.
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là một website cung cấp đầy đủ các tài liệu học tập môn Toán 12, bao gồm sách giáo khoa, sách bài tập, đề thi và lời giải chi tiết. Chúng tôi cam kết cung cấp cho các em những tài liệu chất lượng, chính xác và dễ hiểu nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
Bảng tổng hợp công thức đạo hàm thường dùng
| Hàm số y | Đạo hàm y' |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sin x | y' = cos x |
| y = cos x | y' = -sin x |