Giải bài 3 trang 63 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 3 trang 63 SBT Toán 12 Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết bài 3 trang 63 sách bài tập Toán 12 Chân trời sáng tạo trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp bạn hiểu sâu sắc kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, cập nhật nhanh chóng và hữu ích nhất cho các bạn học sinh.
Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc \({120^ \circ }\) và có độ lớn lần lượt là \(10N\) và \(8N\). Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn \(6N\). Tính độ lớn của hợp lực của ba lực trên.
Đề bài
Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc \({120^ \circ }\) và có độ lớn lần lượt là \(10N\) và \(8N\). Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn \(6N\). Tính độ lớn của hợp lực của ba lực trên.
Phương pháp giải - Xem chi tiết
‒ Sử dụng quy tắc hình bình hành để xác định hợp lực sau đó tính độ lớn của hợp lực.
‒ Sử dụng tích vô hướng của hai vectơ: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết
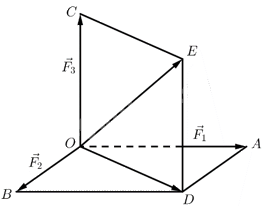
Gọi \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \)lần lượt là ba lực tác động vào một vật đặt tại điểm \(O\).
Ta có \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\overrightarrow {{F_2}} = \overrightarrow {OB} ,\overrightarrow {{F_3}} = \overrightarrow {OC} \).
Độ lớn các lực: \({F_1} = OA = 10N,{F_2} = OB = 8N,{F_3} = OC = 6N\).
Dựng hình bình hành \(OADB\).
Theo quy tắc hình bình hành, ta có \(\overrightarrow {OD} = \overrightarrow {OA} + \overrightarrow {OB} \).
\(\begin{array}{l}{\overrightarrow {OD} ^2} = {\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)^2} = {\overrightarrow {OA} ^2} + 2\overrightarrow {OA} .\overrightarrow {OB} + {\overrightarrow {OB} ^2} = {\left| {\overrightarrow {OA} } \right|^2} + 2\left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) + {\left| {\overrightarrow {OB} } \right|^2}\\ & = {10^2} + 2.10.8.\cos {120^ \circ } + {8^2} = 84\end{array}\)
Dựng hình bình hành \(OCED\).
Tổng lực tác động vào vật là \(\overrightarrow F = \overrightarrow {OE} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \).
Độ lớn của hợp lực tác động vào vật là \(F = OE\).
Theo đề bài ta có \(OC \bot \left( {OADB} \right)\) nên \(OC \bot OD\), suy ra \(ODEC\) là hình chữ nhật.
Do đó tam giác \(ODE\) vuông tại \(D\).
Ta có \(O{E^2} = O{C^2} + O{{\rm{D}}^2} = {6^2} + 84 = 120\).
Vậy \(F = OE = \sqrt {120} = 2\sqrt {30} \approx 10,95\left( N \right)\).
Giải bài 3 trang 63 SBT Toán 12 Chân trời sáng tạo: Tổng quan
Bài 3 trang 63 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit và các phép toán trên hàm số (tổng, hiệu, tích, thương, hàm hợp).
Nội dung chi tiết bài 3 trang 63 SBT Toán 12 Chân trời sáng tạo
Để giải quyết bài 3 trang 63 một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Quy tắc tính đạo hàm: Nắm vững các quy tắc đạo hàm của hàm số cơ bản và quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Các công thức đạo hàm: Thuộc các công thức đạo hàm của các hàm số lượng giác, hàm mũ, hàm logarit.
- Kỹ năng biến đổi đại số: Rèn luyện kỹ năng biến đổi đại số để đơn giản hóa biểu thức trước khi tính đạo hàm.
Lời giải chi tiết bài 3 trang 63 SBT Toán 12 Chân trời sáng tạo
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 3 trang 63 SBT Toán 12 Chân trời sáng tạo:
Câu a)
Đề bài: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1
Lời giải:
f'(x) = 3x2 + 4x - 5
Câu b)
Đề bài: Tính đạo hàm của hàm số g(x) = sin(x) + cos(x)
Lời giải:
g'(x) = cos(x) - sin(x)
Câu c)
Đề bài: Tính đạo hàm của hàm số h(x) = ex + ln(x)
Lời giải:
h'(x) = ex + 1/x
Mẹo giải bài tập đạo hàm hiệu quả
Để giải các bài tập về đạo hàm một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:
- Xác định đúng quy tắc đạo hàm cần sử dụng: Phân tích cấu trúc của hàm số để xác định quy tắc đạo hàm phù hợp.
- Biến đổi đại số trước khi tính đạo hàm: Đơn giản hóa biểu thức bằng cách sử dụng các phép biến đổi đại số.
- Kiểm tra lại kết quả: Sau khi tính đạo hàm, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài tập tương tự
Để củng cố kiến thức về đạo hàm, bạn có thể làm thêm các bài tập tương tự sau:
- Tính đạo hàm của hàm số y = 2x4 - 3x2 + x - 7
- Tính đạo hàm của hàm số y = tan(x) + cot(x)
- Tính đạo hàm của hàm số y = log2(x) + 2x
Kết luận
Hy vọng với lời giải chi tiết và những mẹo giải bài tập trên, bạn đã nắm vững cách giải bài 3 trang 63 SBT Toán 12 Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!
Lưu ý: Nếu bạn gặp bất kỳ khó khăn nào trong quá trình học tập, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.