Đề bài
Người ta đo độ ẩm không khí lúc 12 giờ trưa mỗi ngày tại một địa điểm trong tháng 4. Kết quả các lần đo được biểu diễn ở biểu đồ tần số tương đối ghép nhóm dưới đây.
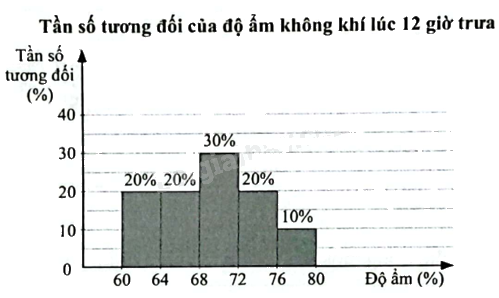
a) Hãy lập bảng tần số ghép nhóm cho dữ liệu ở biểu đồ trên.
b) Hãy tính các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm trên. (Làm tròn kết quả đến hàng phần nghìn.)
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
Tứ phân vị thứ \(k\) được xác định như sau: \({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}\left( {{u_{m + 1}} - {u_m}} \right)\)
trong đó:
• \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu;
• \(\left[ {{u_m};{u_{m + 1}}} \right)\) là nhóm chứa tứ phân vị thứ \(k\);
• \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ \(k\);
• \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1}\).
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\(\begin{array}{l}{S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\\ & = \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + ... + {n_k}c_k^2} \right] - {\overline x ^2}\end{array}\)
‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(S = \sqrt {{S^2}} \).
Lời giải chi tiết
a) Ta có bảng tần số ghép nhóm:
b) Khoảng biến thiên của mẫu số liệu trên là: \(R = 80 - 60 = 30\) (%).
Gọi \({x_1};{x_2};...;{x_{30}}\) là mẫu số liệu gốc theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_8} \in \left[ {64;68} \right)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 64 + \frac{{\frac{{1.30}}{4} - 6}}{6}\left( {68 - 64} \right) = 65\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{23}} \in \left[ {72;76} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 72 + \frac{{\frac{{3.30}}{4} - \left( {6 + 6 + 9} \right)}}{6}\left( {68 - 64} \right) = 73\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\(\Delta Q = {Q_3} - {Q_1} = 73 - 65 = 8\) (%).
Ta có bảng sau:
Cỡ mẫu \(n = 30\)
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{6.62 + 6.66 + 9.70 + 6.74 + 3.78}}{{30}} = 69,2\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\({S^2} = \frac{1}{{30}}\left( {{{6.62}^2} + {{6.66}^2} + {{9.70}^2} + {{6.74}^2} + {{3.78}^2}} \right) - {69,2^2} = 24,96\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(S = \sqrt {24,96} \approx 4,996\).
