Giải bài 6 trang 71 SBT Toán 12 Chân trời sáng tạo

Giải bài 6 trang 71 sách bài tập toán 12 - Chân trời sáng tạo

Giải bài 6 trang 71 sách bài tập Toán 12 Chân trời sáng tạo

Tusach.vn xin giới thiệu lời giải chi tiết bài 6 trang 71 SBT Toán 12 Chân trời sáng tạo. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12 Chân trời sáng tạo, đáp ứng nhu cầu học tập của học sinh.

Cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {2;0;2} \right),B\left( {4;2;4} \right),D\left( {2; - 2;2} \right),C'\left( {8;10; - 10} \right)\). Tìm toạ độ điểm \(A'\).

Đề bài

Cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {2;0;2} \right),B\left( {4;2;4} \right),D\left( {2; - 2;2} \right),C'\left( {8;10; - 10} \right)\). Tìm toạ độ điểm \(A'\).

Phương pháp giải - Xem chi tiết Giải bài 6 trang 71 sách bài tập toán 12 - Chân trời sáng tạo 1

‒ Sử dụng toạ độ của vectơ \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).

‒ Sử dụng tính chất hai vectơ bằng nhau: Với \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\), ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\).

Lời giải chi tiết

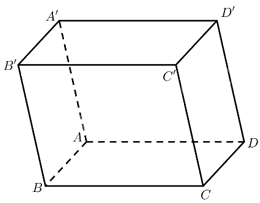
Giải bài 6 trang 71 sách bài tập toán 12 - Chân trời sáng tạo 2

Giả sử \(D\left( {{x_C};{y_C};{z_C}} \right)\). Ta có

\(\overrightarrow {AD} = \left( {2 - 2; - 2 - 0;2 - 2} \right) = \left( {0; - 2;0} \right)\).

\(\overrightarrow {BC} = \left( {{x_C} - 4;{y_C} - 2;{z_C} - 4} \right)\).

\(ABCD\) là hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {BC} \).

\( \Leftrightarrow \left\{ \begin{array}{l}{x_C} - 4 = 0\\{y_C} - 2 = - 2\\{z_C} - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 4\\{y_C} = 0\\{z_C} = 4\end{array} \right.\). Vậy \(C\left( {4;0;4} \right)\).

Giả sử \(A'\left( {{x_{A'}};{y_{A'}};{z_{A'}}} \right)\). Ta có

\(\overrightarrow {AA'} = \left( {{x_{A'}} - 2;{y_{A'}};{z_{A'}} - 2} \right)\).

\(\overrightarrow {CC'} = \left( {8 - 4;10 - 0; - 10 - 4} \right) = \left( {4;10; - 14} \right)\).

\(ABCD\) là hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {BC} \).

\( \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} - 2 = 4\\{y_{A'}} = 10\\{z_{A'}} - 2 = - 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = 6\\{y_{A'}} = 10\\{z_{A'}} = - 12\end{array} \right.\). Vậy \(A'\left( {6;10; - 12} \right)\).

Giải bài 6 trang 71 SBT Toán 12 Chân trời sáng tạo: Tổng quan và hướng dẫn chi tiết

Bài 6 trang 71 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào chủ đề về Đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, phương trình đường thẳng, phương trình mặt phẳng để giải quyết các bài toán liên quan đến vị trí tương đối giữa đường thẳng và mặt phẳng, khoảng cách từ điểm đến mặt phẳng, và các bài toán ứng dụng thực tế.

Nội dung chính của bài 6 trang 71 SBT Toán 12 Chân trời sáng tạo

Kiến thức trọng tâm: Ôn tập lại các công thức tính khoảng cách, phương trình đường thẳng, phương trình mặt phẳng.
Kỹ năng cần thiết: Vận dụng linh hoạt các công thức, phân tích bài toán, lựa chọn phương pháp giải phù hợp.
Loại bài tập thường gặp:
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng.
- Tính khoảng cách từ điểm đến mặt phẳng.
- Tìm giao điểm của đường thẳng và mặt phẳng.
- Lập phương trình đường thẳng, mặt phẳng thỏa mãn các điều kiện cho trước.

Hướng dẫn giải chi tiết bài 6 trang 71 SBT Toán 12 Chân trời sáng tạo

Để giải bài 6 trang 71 SBT Toán 12 Chân trời sáng tạo một cách hiệu quả, bạn cần thực hiện theo các bước sau:

Đọc kỹ đề bài: Xác định rõ các thông tin đã cho và yêu cầu của bài toán.
Phân tích bài toán: Xác định các kiến thức và kỹ năng cần sử dụng để giải bài toán.
Lập kế hoạch giải: Xác định các bước giải cụ thể.
Thực hiện giải: Thực hiện các bước giải theo kế hoạch đã lập.
Kiểm tra lại kết quả: Đảm bảo kết quả giải đúng và hợp lý.

Dưới đây là lời giải chi tiết cho từng phần của bài 6 trang 71 SBT Toán 12 Chân trời sáng tạo:

Ví dụ minh họa (Giả định bài tập cụ thể)

Bài 6a: Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0. Xác định vị trí tương đối giữa đường thẳng d và mặt phẳng (P).

Lời giải:

Ta có vectơ chỉ phương của đường thẳng d là a = (1, -1, 2) và vectơ pháp tuyến của mặt phẳng (P) là n = (2, -1, 1). Ta thấy a.n = 1*2 + (-1)*(-1) + 2*1 = 5 ≠ 0. Do đó, đường thẳng d và mặt phẳng (P) không song song.

Chọn một điểm thuộc đường thẳng d, ví dụ A(1, 2, 3). Thay tọa độ điểm A vào phương trình mặt phẳng (P), ta được: 2*1 - 2 + 3 - 5 = -2 ≠ 0. Do đó, điểm A không thuộc mặt phẳng (P).

Vậy, đường thẳng d cắt mặt phẳng (P).

Mẹo giải nhanh và hiệu quả

Nắm vững các công thức và định lý liên quan đến đường thẳng và mặt phẳng trong không gian.
Luyện tập thường xuyên để rèn luyện kỹ năng giải toán.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm vẽ hình để kiểm tra kết quả.

Tài liệu tham khảo hữu ích

Sách giáo khoa Toán 12 Chân trời sáng tạo
Sách bài tập Toán 12 Chân trời sáng tạo
Các trang web học Toán trực tuyến uy tín

Hy vọng với lời giải chi tiết và hướng dẫn trên, bạn sẽ tự tin giải quyết bài 6 trang 71 SBT Toán 12 Chân trời sáng tạo một cách nhanh chóng và chính xác. Chúc bạn học tốt!