Đề bài
Xét tính đơn điệu và tìm cực trị của các hàm số:
a) \(y = - {x^3} - 3{x^2} + 24x - 1\);
b) \(y = {x^3} - 8{x^2} + 5x + 2\);
c) \(y = {x^3} + 2{x^2} + 3x + 1\);
d) \(y = - 3{x^3} + 3{x^2} - x + 2\).
Phương pháp giải - Xem chi tiết
Các bước để xét tính đơn điệu và tìm cực trị của hàm số \(f\left( x \right)\):
Bước 1. Tìm tập xác định \(D\) của hàm số.
Bước 2. Tính đạo hàm \(f'\left( x \right)\) của hàm số. Tìm các điểm \({x_1},{x_2},...,{x_n} \in D\) mà tại đó đạo hàm \(f'\left( x \right)\) bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm \({x_1},{x_2},...,{x_n}\) theo thứ tự tăng dần, xét dấu \(f'\left( x \right)\) và lập bảng biến thiên.
Bước 4. Nêu kết luận về các khoảng đồng biến, nghịch biến, cực trị của hàm số.
Lời giải chi tiết
a) Xét hàm số \(y = - {x^3} - 3{x^2} + 24x - 1\).
Tập xác định: \(D = \mathbb{R}\).
Ta có \(y' = - 3{x^2} - 6x + 24;y' = 0 \Leftrightarrow x = - 4\) hoặc \(x = 2\).
Bảng biến thiên:

Hàm số đồng biến trên khoảng \(\left( { - 4;2} \right)\), nghịch biến trên các khoảng \(\left( { - \infty ; - 4} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số đạt cực đại tại $x=2,{{y}_{CĐ}}=27$; hàm số đạt cực tiểu tại \(x = - 4,{y_{CT}} = - 81\).
b) Xét hàm số \(y = {x^3} - 8{x^2} + 5x + 2\).
Tập xác định: \(D = \mathbb{R}\).
Ta có \(y' = 3{x^2} - 16x + 5;y' = 0 \Leftrightarrow x = 5\) hoặc \({\rm{x}} = \frac{1}{3}\).
Bảng biến thiên:

Hàm số đồng biến trên các khoảng \(\left( { - \infty ;\frac{1}{3}} \right)\) và \(\left( {5; + \infty } \right)\), nghịch biến trên khoảng \(\left( {\frac{1}{3};5} \right)\).
Hàm số đạt cực đại tại $x=\frac{1}{3},{{y}_{CĐ}}=\frac{76}{27}$; hàm số đạt cực tiểu tại \(x = 5,{y_{CT}} = - 48\).
c) Xét hàm số \(y = {x^3} + 2{x^2} + 3x + 1\).
Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = 3{x^2} + 4x + 3 = 3{\left( {x + \frac{2}{3}} \right)^2} + \frac{5}{3} > 0,\forall x \in \mathbb{R}\)
Bảng biến thiên:

Hàm số đồng biến trên \(\mathbb{R}\).
Hàm số không có cực trị.
d) Xét hàm số \(y = - 3{x^3} + 3{x^2} - x + 2\).
Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = - 9{x^2} + 6x - 1 = - {\left( {3x - 1} \right)^2};y' = 0 \Leftrightarrow x = \frac{1}{3}\).
Bảng biến thiên:
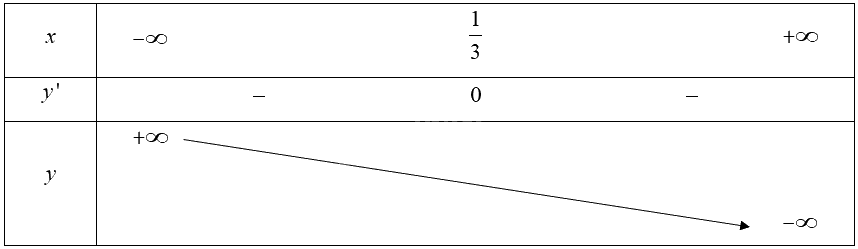
Hàm số nghịch biến trên \(\mathbb{R}\). Hàm số không có cực trị.




