Giải bài 1 trang 21 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 1 trang 21 SBT Toán 12 Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết bài 1 trang 21 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, cập nhật nhanh chóng và đầy đủ nhất để hỗ trợ quá trình học tập của các bạn.
Tìm các tiệm cận của đồ thị hàm số sau:
Đề bài
Tìm các tiệm cận của đồ thị hàm số sau:
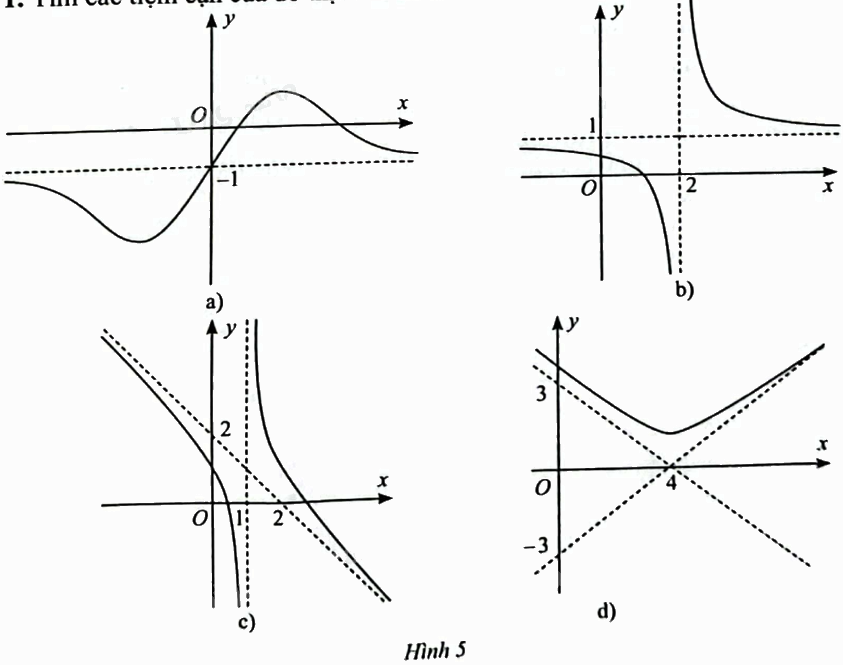
Phương pháp giải - Xem chi tiết
Dựa vào đồ thị hàm số
Lời giải chi tiết
a) ‒ Đồ thị hàm số có tiệm cận ngang là \(y = - 1\);
‒ Đồ thị hàm số không có tiệm cận đứng.
b) Đồ thị hàm số có
‒ Tiệm cận đứng là \(x = 2\).
‒ Tiệm cận ngang là \(y = 1\).
c) Đồ thị hàm số có
‒ Tiệm cận đứng là \(x = 1\).
‒ Tiệm cận xiên là đường thẳng đi qua \(\left( {2;0} \right)\) và \(\left( {0;2} \right)\) (hay đường thẳng \(y = - x + 2\)).
d) Đồ thị hàm số có tiệm cận xiên là đường thẳng đi qua \(\left( {4;0} \right)\) và \(\left( {0;3} \right)\) (hay đường thẳng \(y = - \frac{3}{4}x + 3\)) và đường thẳng đi qua \(\left( {4;0} \right)\) và \(\left( {0; - 3} \right)\) (hay đường thẳng \(y = \frac{3}{4}x - 3\)).
Giải bài 1 trang 21 SBT Toán 12 Chân trời sáng tạo: Chi tiết và Dễ Hiểu
Bài 1 trang 21 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc ôn tập chương 1: Hàm số bậc hai. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về parabol, đỉnh của parabol, trục đối xứng, và các yếu tố ảnh hưởng đến hình dạng của parabol để giải quyết các bài toán thực tế.
Nội dung bài 1 trang 21 SBT Toán 12 Chân trời sáng tạo
Bài 1 thường bao gồm các dạng bài tập sau:
- Xác định các yếu tố của parabol: Tìm tọa độ đỉnh, trục đối xứng, hệ số a, và điểm cắt trục tung của parabol cho trước.
- Viết phương trình parabol: Xác định phương trình parabol khi biết các yếu tố như đỉnh, trục đối xứng, hoặc ba điểm thuộc parabol.
- Ứng dụng parabol vào giải quyết bài toán thực tế: Ví dụ như tìm quỹ đạo của một vật được ném lên, hoặc xác định vị trí tối ưu để đạt được hiệu quả cao nhất.
Hướng dẫn giải chi tiết bài 1 trang 21 SBT Toán 12 Chân trời sáng tạo
Để giải quyết bài 1 trang 21 một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Dạng tổng quát của hàm số bậc hai: y = ax2 + bx + c (a ≠ 0)
- Tọa độ đỉnh của parabol: xđỉnh = -b/2a, yđỉnh = -Δ/4a (với Δ = b2 - 4ac)
- Trục đối xứng của parabol: x = -b/2a
- Điều kiện để parabol cắt trục Ox: Δ > 0
- Điều kiện để parabol tiếp xúc trục Ox: Δ = 0
- Điều kiện để parabol không cắt trục Ox: Δ < 0
Ví dụ minh họa
Bài toán: Tìm tọa độ đỉnh và trục đối xứng của parabol y = 2x2 - 8x + 6.
Giải:
- Hệ số a = 2, b = -8, c = 6
- Tọa độ đỉnh: xđỉnh = -(-8)/(2*2) = 2, yđỉnh = -((-8)2 - 4*2*6)/(4*2) = -1
- Trục đối xứng: x = 2
Lưu ý khi giải bài tập
Khi giải bài tập về hàm số bậc hai, bạn cần chú ý:
- Đọc kỹ đề bài để xác định đúng yêu cầu của bài toán.
- Sử dụng đúng công thức và phương pháp giải.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là địa chỉ tin cậy cung cấp lời giải chi tiết, chính xác và dễ hiểu cho các bài tập Toán 12. Chúng tôi luôn cập nhật nội dung mới nhất và đa dạng các dạng bài tập để giúp bạn học tập hiệu quả. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Chương | Bài | Link |
|---|---|---|
| 1 | Bài 1 | Giải bài 1 trang 21 |
| 1 | Bài 2 | Giải bài 2 trang 21 |