Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 14 trang 12 sách bài tập toán 12 - Chân trời sáng tạo
SBT Toán 12 - Chân trời sáng tạo
SBT TOÁN TẬP 1 - CHÂN TRỜI SÁNG TẠO
Chương 1. Ứng dụng đạo hàm để khảo sát hàm số
Bài 1. Tính đơn điệu và cực trị của hàm số

Giải bài 14 trang 12 sách bài tập toán 12 - Chân trời sáng tạo

Giải bài 14 trang 12 Sách bài tập Toán 12 - Chân trời sáng tạo

Chào mừng bạn đến với lời giải chi tiết bài 14 trang 12 Sách bài tập Toán 12 Chân trời sáng tạo. Tusach.vn cung cấp đáp án chính xác, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập Toán 12.

Chúng tôi luôn cập nhật nhanh chóng và đầy đủ các bài giải SBT Toán 12 Chân trời sáng tạo, hỗ trợ tối đa cho quá trình học tập của bạn.

Một cửa hàng ước tính số lượng sản phẩm \(q\left( {0 \le q \le 100} \right)\) bán được phụ thuộc vào giá bán \(p\) (tính bằng nghìn đồng) theo công thức \(p + 2q = 300\). Chi phí cửa hàng cần chi để nhập về \(q\) sản phẩm là \(C\left( q \right) = 0,05{q^3} - 5,7{q^2} + 295q + 300\) (nghìn đồng). a) Viết công thức tính lợi nhuận \(I\) của cửa hàng khi nhập về và bán được \(q\) sản phẩm. b) Trong khoảng nào của \(q\) thì lợi nhuận sẽ tăng khi \(q\) tăng, trong khoảng nào thì lợi nhuận giảm kh

Đề bài

Một cửa hàng ước tính số lượng sản phẩm \(q\left( {0 \le q \le 100} \right)\) bán được phụ thuộc vào giá bán \(p\) (tính bằng nghìn đồng) theo công thức \(p + 2q = 300\). Chi phí cửa hàng cần chi để nhập về \(q\) sản phẩm là

\(C\left( q \right) = 0,05{q^3} - 5,7{q^2} + 295q + 300\) (nghìn đồng).

a) Viết công thức tính lợi nhuận \(I\) của cửa hàng khi nhập về và bán được \(q\) sản phẩm.

b) Trong khoảng nào của \(q\) thì lợi nhuận sẽ tăng khi \(q\) tăng, trong khoảng nào thì lợi nhuận giảm khi \(q\) tăng?

Phương pháp giải - Xem chi tiếtGiải bài 14 trang 12 sách bài tập toán 12 - Chân trời sáng tạo 1

• \(I = pq - C\).

• Xét hàm số \(I\left( q \right)\) trên đoạn $\left[ 0;100 \right]$, lập bảng biến thiên và tìm khoảng đồng biến, nghịch biến của hàm số.

Lời giải chi tiết

a) \(p + 2q = 300 \Leftrightarrow p = 300 - 2q\)

\(I = pq - C = \left( {300 - 2q} \right).q - \left( {0,05{q^3} - 5,7{q^2} + 295q + 300} \right) = - 0,05{q^3} + 3,7{q^2} + 5q - 300\).

b) Xét hàm số \(I\left( q \right) = - 0,05{q^3} + 3,7{q^2} + 5q - 300\) trên đoạn \(\left[ {0;100} \right]\).

Ta có:

\(I'\left( q \right) = - 0,15{q^2} + 7,4q + 5;I'\left( q \right) = 0 \Leftrightarrow q = 50\) hoặc \(q = - \frac{2}{3}\) (loại).

Bảng biến thiên:

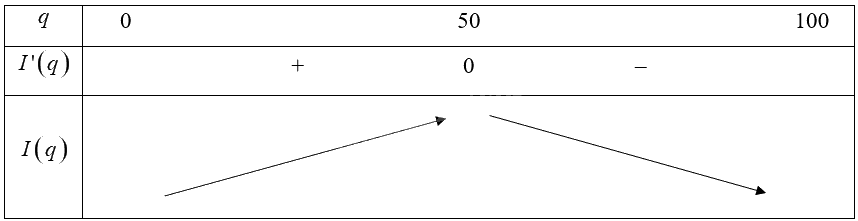
Giải bài 14 trang 12 sách bài tập toán 12 - Chân trời sáng tạo 2

Vậy hàm số đồng biến trên khoảng \(\left( {0;50} \right)\), hàm số nghịch biến trên khoảng \(\left( {50;100} \right)\).

Vậy trong khoảng \(\left( {0;50} \right)\) lợi nhuận sẽ tăng khi \(q\) tăng, trong khoảng \(\left( {50;100} \right)\) lợi nhuận sẽ giảm khi \(q\) tăng.

Giải bài 14 trang 12 Sách bài tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp giải

Bài 14 trang 12 Sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh vận dụng các công thức đạo hàm cơ bản, quy tắc tính đạo hàm của hàm hợp, và các phương pháp tìm cực trị, điểm uốn của hàm số.

Nội dung chi tiết bài 14 trang 12

Bài 14 thường bao gồm các dạng bài tập sau:

  • Dạng 1: Tính đạo hàm của hàm số. Yêu cầu tính đạo hàm bậc nhất, bậc hai của hàm số cho trước.
  • Dạng 2: Khảo sát hàm số. Xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn của hàm số.
  • Dạng 3: Ứng dụng đạo hàm để giải các bài toán thực tế. Ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.

Lời giải chi tiết bài 14 trang 12 (Ví dụ)

Bài 14.1: Tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1.

Lời giải:

f'(x) = 3x2 - 6x + 2

Phương pháp giải bài tập đạo hàm hiệu quả

  1. Nắm vững các công thức đạo hàm cơ bản: Đạo hàm của xn, sinx, cosx, tanx, ex, ln(x),...
  2. Thành thạo các quy tắc tính đạo hàm: Quy tắc cộng, trừ, nhân, chia, đạo hàm hàm hợp.
  3. Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
  4. Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi có chức năng tính đạo hàm, các phần mềm giải toán online.

Tại sao nên chọn tusach.vn để giải bài tập Toán 12?

  • Đáp án chính xác, nhanh chóng: Chúng tôi luôn cập nhật đáp án mới nhất và kiểm tra kỹ lưỡng trước khi đăng tải.
  • Lời giải chi tiết, dễ hiểu: Giải thích từng bước, giúp bạn hiểu rõ bản chất của bài toán.
  • Giao diện thân thiện, dễ sử dụng: Tìm kiếm bài tập nhanh chóng, dễ dàng.
  • Hỗ trợ 24/7: Đội ngũ tư vấn nhiệt tình, sẵn sàng giải đáp mọi thắc mắc của bạn.

Các bài tập liên quan

Ngoài bài 14 trang 12, tusach.vn còn cung cấp lời giải chi tiết cho các bài tập khác trong Sách bài tập Toán 12 Chân trời sáng tạo. Bạn có thể tìm kiếm theo số bài, số trang hoặc theo chủ đề để tìm được bài tập mình cần.

Kết luận

Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà tusach.vn cung cấp, bạn sẽ tự tin hơn trong việc học tập môn Toán 12. Chúc bạn học tốt!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN