Lý Thuyết Tọa Độ Vectơ Toán 12 Cánh Diều

Lý thuyết Tọa độ của vecto Toán 12 Cánh Diều

Lý thuyết Tọa độ của Vectơ Toán 12 Cánh Diều

Bài học này cung cấp đầy đủ kiến thức về tọa độ của vectơ trong không gian, một phần quan trọng của chương trình Toán 12 Cánh Diều.

Chúng ta sẽ cùng tìm hiểu cách biểu diễn vectơ bằng tọa độ, các phép toán trên vectơ biểu diễn bằng tọa độ, và ứng dụng của chúng trong giải quyết các bài toán hình học.

Tusach.vn cam kết cung cấp nội dung chính xác, dễ hiểu, giúp bạn tự tin chinh phục môn Toán.

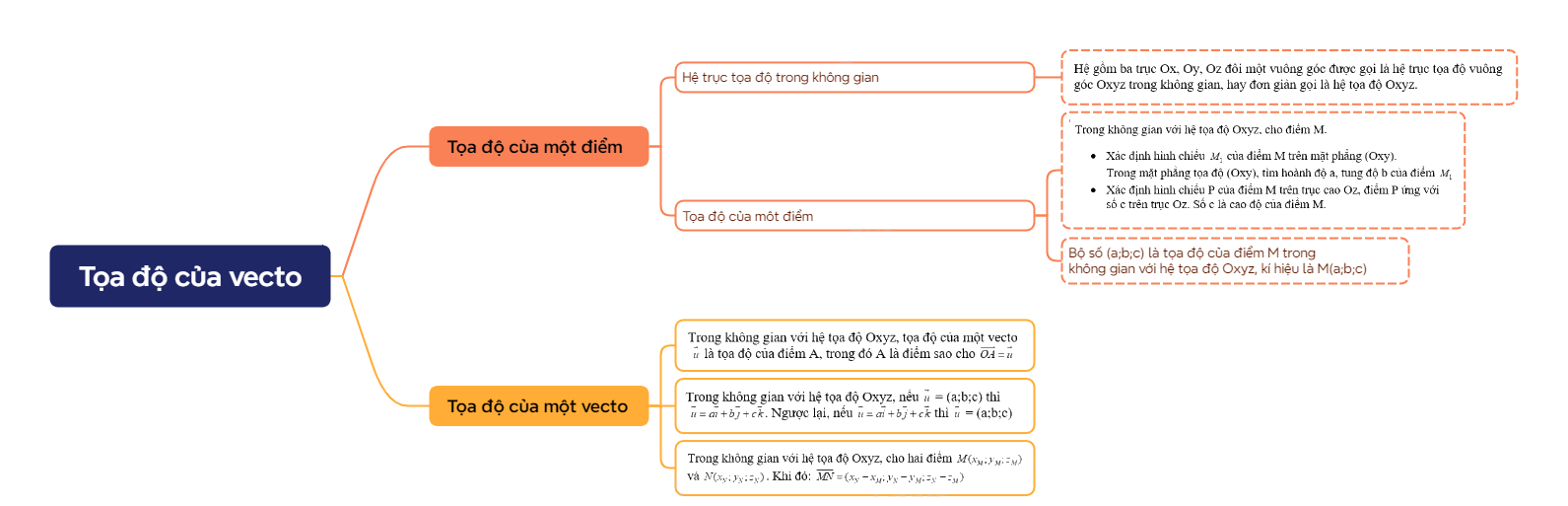
1. Tọa độ của một điểm a) Hệ trục tọa độ trong không gian

1. Tọa độ của một điểm

a) Hệ trục tọa độ trong không gian

Hệ gồm ba trục Ox, Oy, Oz đôi một vuông góc được gọi là hệ trục tọa độ vuông góc Oxyz trong không gian, hay đơn giản gọi là hệ tọa độ Oxyz.

b) Tọa độ của một điểm

Trong không gian với hệ tọa độ Oxyz, cho điểm M.

- Xác định hình chiếu \({M_1}\) của điểm M trên mặt phẳng (Oxy). Trong mặt phẳng tọa độ (Oxy), tìm hoành độ a, tung độ b của điểm \({M_1}\)

- Xác định hình chiếu P của điểm M trên trục cao Oz, điểm P ứng với số c trên trục Oz. Số c là cao độ của điểm M.

Bộ số (a;b;c) là tọa độ của điểm M trong không gian với hệ tọa độ Oxyz, kí hiệu là M(a;b;c)

2. Tọa độ của một vecto

Tọa độ của điểm M được gọi là tọa độ của vecto \(\overrightarrow {OM} \)

Trong không gian với hệ tọa độ Oxyz, tọa độ của một vecto \(\overrightarrow u \) là tọa độ của điểm A, trong đó A là điểm sao cho \(\overrightarrow {OA} = \overrightarrow u \)

Trong không gian với hệ tọa độ Oxyz, nếu \(\overrightarrow u \) = (a;b;c) thì \[\overrightarrow u = a\overrightarrow i + b\overrightarrow j + c\overrightarrow k \] .

Ngược lại, nếu \[\overrightarrow u = a\overrightarrow i + b\overrightarrow j + c\overrightarrow k \] thì \(\overrightarrow u \) = (a;b;c)

Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(M({x_M};{y_M};{z_M})\) và \(N({x_N};{y_N};{z_N})\). Khi đó: \(\overrightarrow {MN} = ({x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M})\)

Ví dụ: Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A’B’C có A(1;0;2), B(3;2;5), C(7;-3;9)

a) Tìm tọa độ của \(\overrightarrow {AA'} \)

b) Tìm tọa độ của các điểm B’, C’

Lời giải

a) Ta có: \(\overrightarrow {AA'} = ({x_{A'}} - {x_A};{y_{A'}} - {y_A};{z_{A'}} - {z_A}) = (4;0; - 1)\)

b) Gọi tọa độ của điểm B’ là (x,y,z) thì \(\overrightarrow {BB'} \) = (x-3;y-2;z-5). Vì ABC.A’B’C’ là hình lăng trụ nên ABB’A’ là hình bình hành, suy ra \(\overrightarrow {AA'} \) = \(\overrightarrow {BB'} \)

Do đó \(\left\{ \begin{array}{l}x - 3 = 4\\y - 2 = 0\\z - 5 = - 1\end{array} \right.\) hay x = 7, y = 2, z = 4. Vậy B’(7;2;4)

Lập luận tương tự suy ra C’(11;-3;8)

Lý thuyết Tọa độ của vecto Toán 12 Cánh Diều 1

Lý Thuyết Tọa Độ Vectơ Toán 12 Cánh Diều: Tổng Quan và Ứng Dụng

Trong chương trình Toán 12, đặc biệt là sách Cánh Diều, kiến thức về tọa độ vectơ đóng vai trò then chốt trong việc giải quyết các bài toán hình học không gian. Bài viết này sẽ cung cấp một cái nhìn toàn diện về lý thuyết này, từ định nghĩa cơ bản đến các ứng dụng thực tế.

1. Định Nghĩa và Biểu Diễn Vectơ Bằng Tọa Độ

Một vectơ trong không gian được xác định bởi độ dài và hướng. Để biểu diễn vectơ một cách định lượng, chúng ta sử dụng tọa độ. Trong không gian hai chiều (mặt phẳng), một vectơ a được biểu diễn bằng cặp số (x; y), trong đó x là hoành độ và y là tung độ của vectơ. Tương tự, trong không gian ba chiều, vectơ a được biểu diễn bằng bộ ba số (x; y; z).

2. Các Phép Toán Trên Vectơ Biểu Diễn Bằng Tọa Độ

Khi vectơ được biểu diễn bằng tọa độ, các phép toán cộng, trừ, nhân với một số thực trở nên đơn giản hơn nhiều:

Phép cộng vectơ: Nếu a = (x₁; y₁) và b = (x₂; y₂), thì a + b = (x₁ + x₂; y₁ + y₂).
Phép trừ vectơ: Nếu a = (x₁; y₁) và b = (x₂; y₂), thì a - b = (x₁ - x₂; y₁ - y₂).
Phép nhân vectơ với một số thực: Nếu a = (x; y) và k là một số thực, thì ka = (kx; ky).

3. Tích Vô Hướng của Hai Vectơ

Tích vô hướng của hai vectơ a và b, ký hiệu là a.b, là một số thực được tính bằng tổng tích các hoành độ và tung độ tương ứng của hai vectơ. Công thức:

a.b = x₁x₂ + y₁y₂ (trong không gian hai chiều)

Tích vô hướng có nhiều ứng dụng quan trọng, như tính góc giữa hai vectơ, kiểm tra tính vuông góc của hai vectơ.

4. Ứng Dụng của Tọa Độ Vectơ trong Giải Toán Hình Học

Tọa độ vectơ là công cụ mạnh mẽ để giải quyết các bài toán hình học:

Chứng minh các đẳng thức vectơ: Sử dụng các phép toán trên tọa độ vectơ để biến đổi và chứng minh các đẳng thức.
Tìm tọa độ của các điểm: Dựa vào các mối quan hệ giữa các vectơ và các điểm để tìm tọa độ của các điểm chưa biết.
Tính diện tích và khoảng cách: Sử dụng tích vô hướng và các công thức liên quan để tính diện tích tam giác, khoảng cách giữa hai điểm.

5. Bài Tập Ví Dụ Minh Họa

Bài tập 1: Cho A(1; 2) và B(3; 4). Tìm tọa độ của vectơ AB.

Giải:AB = (3 - 1; 4 - 2) = (2; 2).

Bài tập 2: Cho a = (1; -2) và b = (3; 1). Tính a.b.

Giải:a.b = (1)(3) + (-2)(1) = 3 - 2 = 1.

6. Lời Khuyên Khi Học Lý Thuyết Tọa Độ Vectơ

Nắm vững định nghĩa và các phép toán cơ bản trên vectơ.
Luyện tập thường xuyên với các bài tập đa dạng.
Hiểu rõ ứng dụng của tọa độ vectơ trong giải quyết các bài toán hình học.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ hình để kiểm tra kết quả.

Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn đầy đủ và chi tiết về lý thuyết tọa độ vectơ Toán 12 Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao!