Giải Bài Tập Toán 12 Trang 48 SGK Tập 1 - Cánh Diều

Giải bài tập 12 trang 48 SGK Toán 12 tập 1 - Cánh diều

Giải Bài Tập Toán 12 Trang 48 SGK Tập 1 - Cánh Diều

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 1 - Cánh Diều. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài tập 12 trang 48, từ đó củng cố kiến thức và tự tin hơn trong quá trình học tập.

Chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất, kèm theo các lưu ý quan trọng để bạn có thể áp dụng vào các bài tập tương tự.

Một bác nông dân có ba tấm lưới thép B40, mỗi tấm dài a (m) và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân ABCD (bờ sông là đường thẳng CD không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?

Đề bài

Phương pháp giải - Xem chi tiết Giải bài tập 12 trang 48 SGK Toán 12 tập 1 - Cánh diều 1

Phân tích đề bài.

Tìm các mối quan hệ trong bài.

Lập phương trình và giải.

Lời giải chi tiết

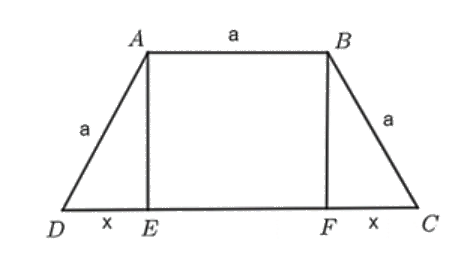
Giải bài tập 12 trang 48 SGK Toán 12 tập 1 - Cánh diều 2

Dựng các đường cao AE và BF của hình thang cân ABCD như hình vẽ trên.

Vì ABCD là hình thang cân nên DE = FC và EF = AB = a.

Đặt DE = FC = x (m) (x > 0).

Ta có DC = DE + EF + FC = x + a + x = 2x + a.

Theo định lí Pythagore, ta suy ra \(AE = \sqrt {A{D^2} - D{E^2}} = \sqrt {{a^2} - {x^2}} \) (m).

Rõ ràng, x phải thỏa mãn điều kiện 0 < x < a.

Diện tích của hình thang cân ABCD là:

\(S = \frac{1}{2}(AB + CD)AE = \frac{1}{2}(a + 2x + a)\sqrt {{a^2} - {x^2}} = (a + x)\sqrt {{a^2} - {x^2}} \) (m²).

Xét hàm số \(S(x) = (a + x)\sqrt {{a^2} - {x^2}} \) với \(x \in (0;a)\).

Ta có \(S'(x) = \frac{{ - 2{x^2} - ax + {a^2}}}{{\sqrt {{a^2} - {x^2}} }} = 0 \Leftrightarrow - 2{x^2} - ax + {a^2} = 0 \Leftrightarrow (x + a)(a - 2x) = 0\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - a}\\{x = \frac{a}{2}}\end{array}} \right.\)

Khi đó trên khoảng (0;a), S’(x) = 0 khi \(x = \frac{a}{2}\).

Ta có bảng biến thiên:

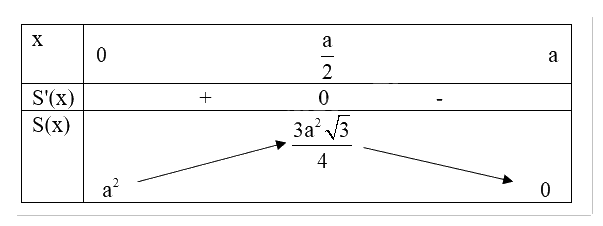
Giải bài tập 12 trang 48 SGK Toán 12 tập 1 - Cánh diều 3

Căn cứ vào bảng biến thiên, ta thấy hàm số S(x) đạt giá trị lớn nhất bằng \(\frac{{3{a^2}\sqrt 3 }}{4}\) tại \(x = \frac{a}{2}\).

Vậy bác đó có thể rào được mảnh vườn có diện tích lớn nhất là \(\frac{{3{a^2}\sqrt 3 }}{4}\) (m²).

Giải Bài Tập 12 Trang 48 SGK Toán 12 Tập 1 - Cánh Diều: Hướng Dẫn Chi Tiết

Bài tập 12 trang 48 SGK Toán 12 tập 1 - Cánh Diều thuộc chương trình học về đạo hàm. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học nâng cao hơn. Bài tập này thường yêu cầu học sinh vận dụng các công thức và quy tắc đạo hàm đã học để giải quyết các bài toán cụ thể.

Nội Dung Bài Tập 12 Trang 48

Bài tập 12 thường bao gồm các dạng bài sau:

Tính đạo hàm của hàm số tại một điểm cho trước.
Tìm đạo hàm của hàm số.
Áp dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số.
Khảo sát hàm số bằng đạo hàm (xác định khoảng đồng biến, nghịch biến, cực trị).

Lời Giải Chi Tiết Bài Tập 12 Trang 48

Để giải bài tập 12 trang 48 SGK Toán 12 tập 1 - Cánh Diều, bạn cần nắm vững các kiến thức sau:

Các công thức đạo hàm cơ bản: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit.
Các quy tắc đạo hàm: Quy tắc cộng, trừ, nhân, chia, quy tắc hàm hợp.
Ứng dụng của đạo hàm: Tìm cực trị, khảo sát hàm số.

Dưới đây là ví dụ về cách giải một dạng bài tập thường gặp trong bài tập 12:

Ví dụ: Tính đạo hàm của hàm số f(x) = x³ + 2x² - 5x + 1

Lời giải:

f'(x) = 3x² + 4x - 5

Lưu Ý Khi Giải Bài Tập Đạo Hàm

Luôn kiểm tra lại kết quả sau khi tính đạo hàm.
Sử dụng các công thức đạo hàm một cách chính xác.
Chú ý đến các quy tắc đạo hàm khi tính đạo hàm của hàm số phức tạp.
Rèn luyện thường xuyên để nắm vững kiến thức và kỹ năng giải bài tập.

Tusach.vn - Đồng Hành Cùng Bạn Trong Học Tập

Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong SGK Toán 12 tập 1 - Cánh Diều. Chúng tôi hy vọng rằng với sự hỗ trợ của tusach.vn, bạn sẽ học tập hiệu quả và đạt được kết quả tốt nhất.

Bảng Tổng Hợp Công Thức Đạo Hàm Cơ Bản

Hàm số y = f(x)	Đạo hàm y' = f'(x)
C (hằng số)	0
xⁿ	nx^n-1
sin x	cos x
cos x	-sin x

Hãy truy cập tusach.vn thường xuyên để cập nhật thêm nhiều kiến thức và bài tập hữu ích khác!

Giải bài tập 12 trang 48 SGK Toán 12 tập 1 - Cánh diều