Giải mục 1 trang 5, 6, 7 SGK Toán 12 tập 1 - Cánh diều
Tổng quan nội dung
Giải mục 1 trang 5, 6, 7 SGK Toán 12 tập 1 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 5, 6, 7 SGK Toán 12 tập 1 - Cánh Diều. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài học, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong các kỳ thi.
Nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 7 SGK Toán 12 Cánh diều
a) Xác định tính đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^3}\).
b) Xét dấu của đạo hàm \(f'\left( x \right) = 3{x^2}\).
c) Phương trình \(f'\left( x \right) = 0\) có bao nhiêu nghiệm ?
Phương pháp giải:
Dựa vào định nghĩa đồng biến, nghịch biến của hàm số và các bước xét tính đồng biến, nghịch biến của hàm số
Lời giải chi tiết:
a) Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 3{x^2}\).
Xét \(y' = 0 \Rightarrow x = 0\).
Bảng biến thiên:
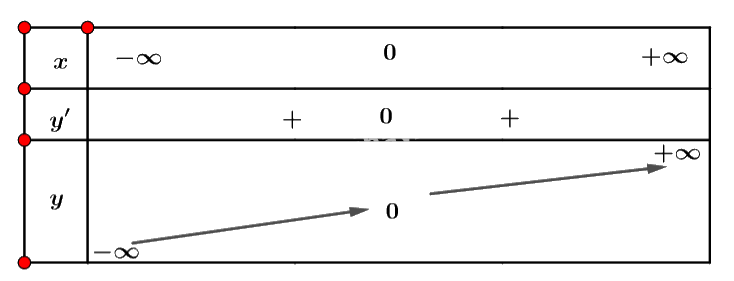
Vậy hàm số đồng biến trên \(\mathbb{R}\).
b) Dựa vào bảng biến thiên ta thấy đạo hàm \(y' = 3{x^2}\) luôn dương với mọi x.
c) Phương trình \(f'\left( x \right) = 0\) có một nghiệm.
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 5 SGK Toán 12 Cánh diều
a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập \(K \subset \mathbb{R}\), trong đó K là một khoảng, đoạn hoặc nửa khoảng.
b) Cho hàm số \(y = f\left( x \right) = {x^2}\) có đồ thị như Hình 2.
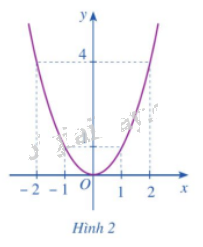
- Xác định khoảng đồng biến, nghịch biến của hàm số đó.
- Xét dấu đạo hàm \(f'\left( x \right) = 2x\).
- Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^2}\) và dấu của đạo hàm \(f'\left( x \right) = 2x\) trên mỗi khoảng \(\left( { - \infty ;0} \right),\left( {0; + \infty } \right)\).
- Hoàn thành bảng biến thiên sau:

Phương pháp giải:
Dựa vào định nghĩa hàm số đồng biến, nghịch biến trên tập K
Lời giải chi tiết:
a) Cho K là một khoảng, một đoạn hoặc một nửa khoảng và \(f\left( x \right)\) là hàm số xác định trên K.
- Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
- Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
- Hàm số đồng biến hoặc nghịch biến trên K còn được gọi là hàm số đơn điệu trên K.
b)
- Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
- Đạo hàm \(f'\left( x \right) = 2x\)âm khi \(x < 0\) và dương khi \(x > 0\).
- Hàm số \(y = f\left( x \right) = {x^2}\) nghịch biến khi \(f'\left( x \right) = 2x\)mang dấu âm và đồng biến khi \(f'\left( x \right) = 2x\) mang dấu dương.
- Ta có bàng biến thiên sau:
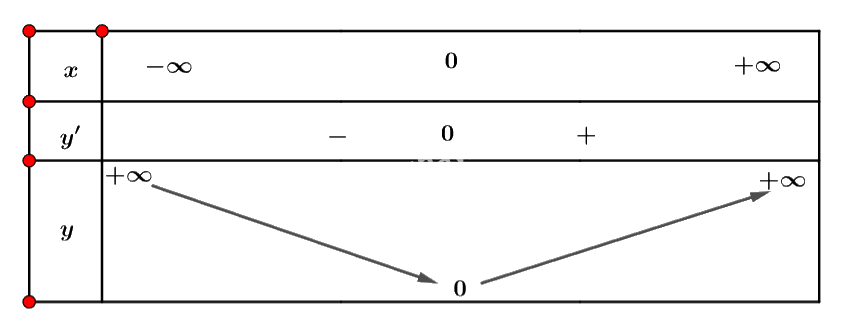
LT2
Trả lời câu hỏi Luyện tập 2 trang 7 SGK Toán 12 Cánh diều
Tìm các khoảng đơn điệu của hàm số \(y = {x^4} + 2{x^2} - 3\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^3} + 4x\).
Xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên:
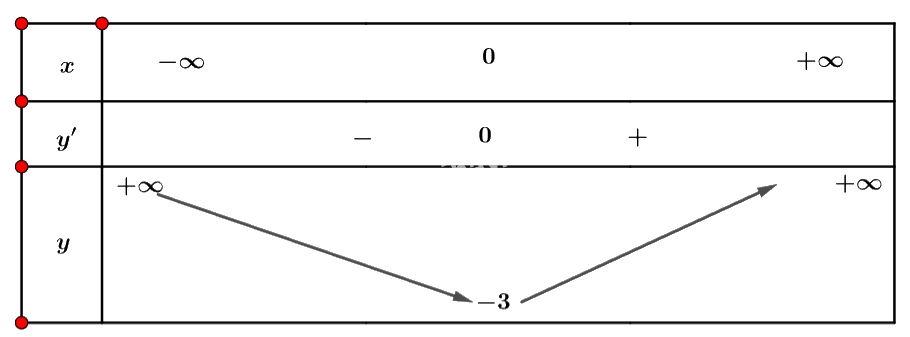
Vậy hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
LT3
Trả lời câu hỏi Luyện tập 3 trang 7 SGK Toán 12 Cánh diều
Chứng minh rằng hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( - \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = \frac{x}{{\sqrt {{x^2} + 1} }}\).
Xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên:
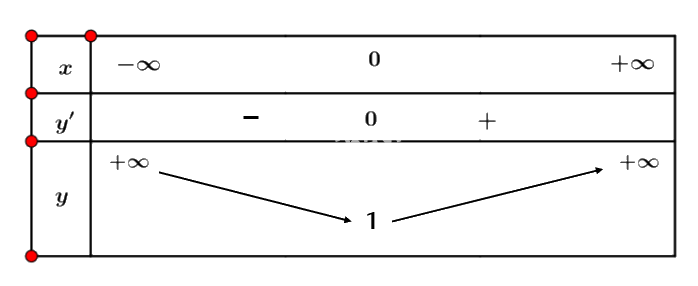
Vậy hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( - \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).
LT4
Trả lời câu hỏi Luyện tập 4 trang 8 SGK Toán 12 Cánh diều
Tìm các khoảng đơn điệu của hàm số sau \(y = \frac{{2x - 1}}{{x + 2}}\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{5}{{{{\left( {x + 2} \right)}^2}}}\).
Nhận xét: \(y' > 0\) với mọi \(x \in D\).
Ta có bảng biến thiên:
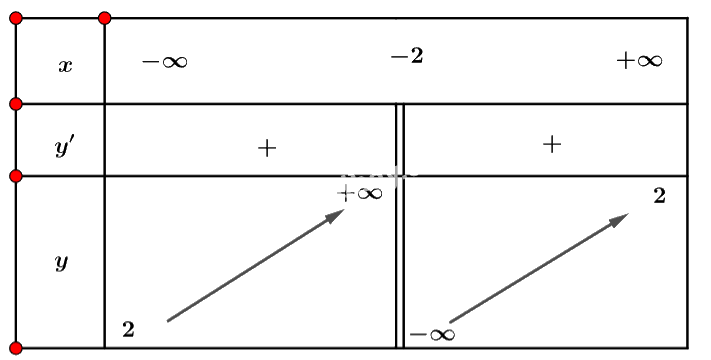
Vậy hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
LT1
Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 12 Cánh diều
Xét dấu \(y'\) rồi tìm khoảng đồng biến, nghịch biến của hàm số\(y = \frac{4}{3}{x^3} - 2{x^2} + x - 1\).
Phương pháp giải:
B1: Tính \(y'\)rồi lập bảng xét dấu của \(y'\).
B2. Dựa vào bảng xét dấu của \(y'\) để nhận xét khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^2} - 4x + 1\).
Xét \(y' = 0 \Leftrightarrow x = \frac{1}{2}\).

Vậy hàm số đồng biến trên \(\mathbb{R}\).
- HĐ1
- LT1
- LT2
- HĐ2
- LT3
- LT4
Trả lời câu hỏi Hoạt động 1 trang 5 SGK Toán 12 Cánh diều
a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập \(K \subset \mathbb{R}\), trong đó K là một khoảng, đoạn hoặc nửa khoảng.
b) Cho hàm số \(y = f\left( x \right) = {x^2}\) có đồ thị như Hình 2.
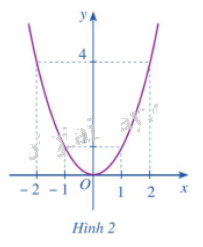
- Xác định khoảng đồng biến, nghịch biến của hàm số đó.
- Xét dấu đạo hàm \(f'\left( x \right) = 2x\).
- Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^2}\) và dấu của đạo hàm \(f'\left( x \right) = 2x\) trên mỗi khoảng \(\left( { - \infty ;0} \right),\left( {0; + \infty } \right)\).
- Hoàn thành bảng biến thiên sau:

Phương pháp giải:
Dựa vào định nghĩa hàm số đồng biến, nghịch biến trên tập K
Lời giải chi tiết:
a) Cho K là một khoảng, một đoạn hoặc một nửa khoảng và \(f\left( x \right)\) là hàm số xác định trên K.
- Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
- Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
- Hàm số đồng biến hoặc nghịch biến trên K còn được gọi là hàm số đơn điệu trên K.
b)
- Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
- Đạo hàm \(f'\left( x \right) = 2x\)âm khi \(x < 0\) và dương khi \(x > 0\).
- Hàm số \(y = f\left( x \right) = {x^2}\) nghịch biến khi \(f'\left( x \right) = 2x\)mang dấu âm và đồng biến khi \(f'\left( x \right) = 2x\) mang dấu dương.
- Ta có bàng biến thiên sau:
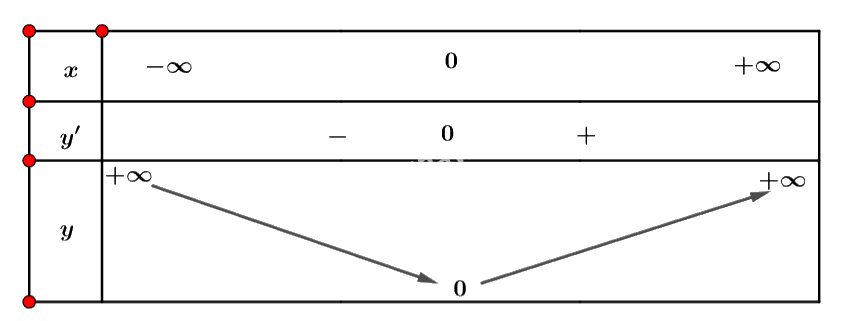
Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 12 Cánh diều
Xét dấu \(y'\) rồi tìm khoảng đồng biến, nghịch biến của hàm số\(y = \frac{4}{3}{x^3} - 2{x^2} + x - 1\).
Phương pháp giải:
B1: Tính \(y'\)rồi lập bảng xét dấu của \(y'\).
B2. Dựa vào bảng xét dấu của \(y'\) để nhận xét khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^2} - 4x + 1\).
Xét \(y' = 0 \Leftrightarrow x = \frac{1}{2}\).

Vậy hàm số đồng biến trên \(\mathbb{R}\).
Trả lời câu hỏi Luyện tập 2 trang 7 SGK Toán 12 Cánh diều
Tìm các khoảng đơn điệu của hàm số \(y = {x^4} + 2{x^2} - 3\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^3} + 4x\).
Xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên:
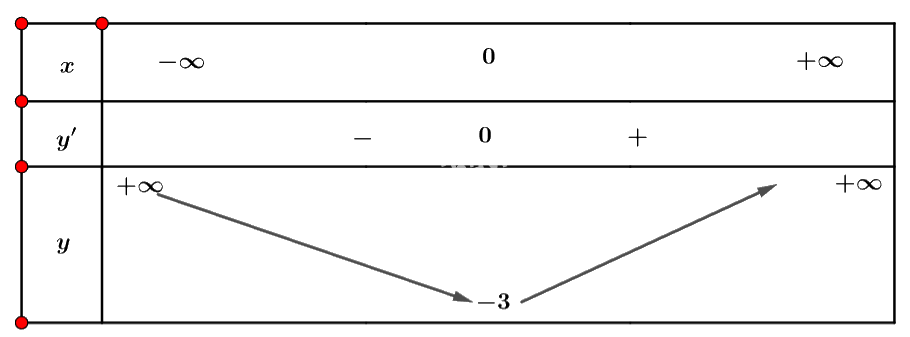
Vậy hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
Trả lời câu hỏi Hoạt động 2 trang 7 SGK Toán 12 Cánh diều
a) Xác định tính đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^3}\).
b) Xét dấu của đạo hàm \(f'\left( x \right) = 3{x^2}\).
c) Phương trình \(f'\left( x \right) = 0\) có bao nhiêu nghiệm ?
Phương pháp giải:
Dựa vào định nghĩa đồng biến, nghịch biến của hàm số và các bước xét tính đồng biến, nghịch biến của hàm số
Lời giải chi tiết:
a) Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 3{x^2}\).
Xét \(y' = 0 \Rightarrow x = 0\).
Bảng biến thiên:
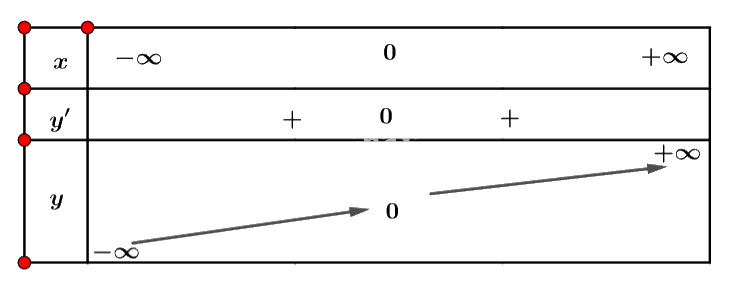
Vậy hàm số đồng biến trên \(\mathbb{R}\).
b) Dựa vào bảng biến thiên ta thấy đạo hàm \(y' = 3{x^2}\) luôn dương với mọi x.
c) Phương trình \(f'\left( x \right) = 0\) có một nghiệm.
Trả lời câu hỏi Luyện tập 3 trang 7 SGK Toán 12 Cánh diều
Chứng minh rằng hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( - \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = \frac{x}{{\sqrt {{x^2} + 1} }}\).
Xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên:
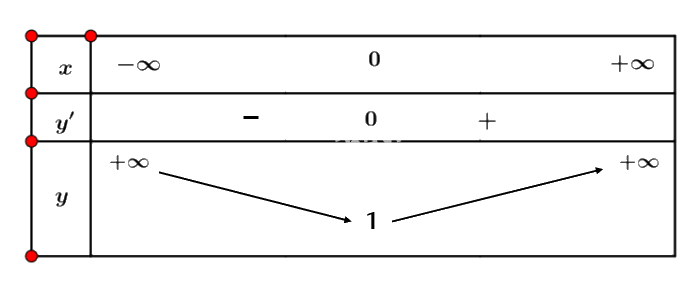
Vậy hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( - \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).
Trả lời câu hỏi Luyện tập 4 trang 8 SGK Toán 12 Cánh diều
Tìm các khoảng đơn điệu của hàm số sau \(y = \frac{{2x - 1}}{{x + 2}}\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{5}{{{{\left( {x + 2} \right)}^2}}}\).
Nhận xét: \(y' > 0\) với mọi \(x \in D\).
Ta có bảng biến thiên:
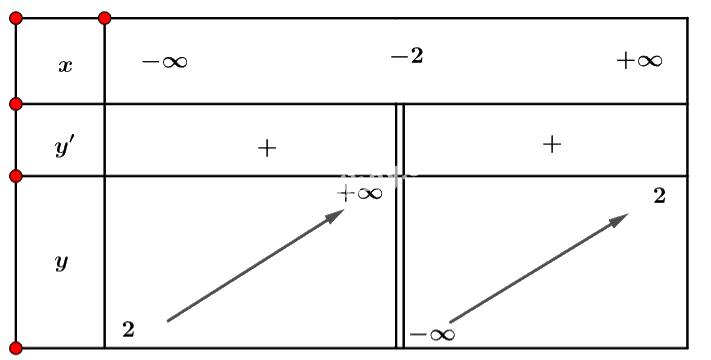
Vậy hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
Giải mục 1 trang 5, 6, 7 SGK Toán 12 tập 1 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Mục 1 của chương trình Toán 12 tập 1 - Cánh Diều tập trung vào việc ôn tập và mở rộng kiến thức về hàm số và đồ thị. Đây là nền tảng quan trọng cho các kiến thức nâng cao hơn trong chương trình học. Bài tập trong mục này giúp học sinh củng cố lý thuyết, rèn luyện kỹ năng vẽ đồ thị và giải các bài toán liên quan đến hàm số.
Nội dung chính của Mục 1
- Ôn tập về hàm số: Các loại hàm số (hàm số bậc nhất, hàm số bậc hai, hàm số mũ, hàm số logarit), tập xác định, tập giá trị, tính đơn điệu, cực trị.
- Đồ thị hàm số: Cách vẽ đồ thị hàm số, các điểm đặc biệt trên đồ thị (điểm cực trị, điểm uốn, giao điểm với các trục tọa độ).
- Ứng dụng của hàm số: Giải các bài toán thực tế liên quan đến hàm số.
Giải chi tiết bài tập trang 5, 6, 7 SGK Toán 12 tập 1 - Cánh Diều
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 5, 6, 7 SGK Toán 12 tập 1 - Cánh Diều:
Bài 1: (Trang 5)
(Nêu lại đề bài)
Lời giải:
(Giải chi tiết bài tập, bao gồm các bước giải, lý thuyết áp dụng và kết luận)
Bài 2: (Trang 6)
(Nêu lại đề bài)
Lời giải:
(Giải chi tiết bài tập, bao gồm các bước giải, lý thuyết áp dụng và kết luận)
Bài 3: (Trang 7)
(Nêu lại đề bài)
Lời giải:
(Giải chi tiết bài tập, bao gồm các bước giải, lý thuyết áp dụng và kết luận)
Mẹo giải bài tập hàm số hiệu quả
- Nắm vững lý thuyết: Hiểu rõ định nghĩa, tính chất và các công thức liên quan đến hàm số.
- Vẽ đồ thị: Sử dụng đồ thị để hình dung rõ hơn về hàm số và tìm ra các điểm đặc biệt.
- Phân tích bài toán: Xác định rõ yêu cầu của bài toán và lựa chọn phương pháp giải phù hợp.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả của bạn là chính xác và hợp lý.
Tài liệu tham khảo hữu ích
Ngoài SGK Toán 12 tập 1 - Cánh Diều, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức:
- Sách bài tập Toán 12
- Các trang web học toán trực tuyến
- Các video bài giảng trên YouTube
Tusach.vn hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc giải các bài tập Toán 12 tập 1 - Cánh Diều. Chúc các em học tập tốt!
| Bài tập | Trang | Độ khó |
|---|---|---|
| Bài 1 | 5 | Dễ |
| Bài 2 | 6 | Trung bình |
| Bài 3 | 7 | Khó |