Giải mục 1 trang 50, 51, 52 SGK Toán 12 tập 2 - Cánh diều
Tổng quan nội dung
Giải mục 1 trang 50, 51, 52 SGK Toán 12 tập 2 - Cánh diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 50, 51, 52 SGK Toán 12 tập 2 chương trình Cánh diều. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và lời giải dễ hiểu nhất.
Bài tập này thuộc chương trình học Toán 12 tập 2, tập trung vào các kiến thức về tích phân và ứng dụng của tích phân.
Vecto pháp tuyến. Cặp vecto chỉ phương của mặt phẳng
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 50 SGK Toán 12 Cánh diều
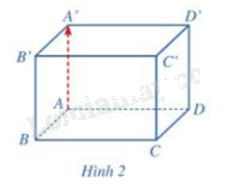
Cho hình hộp chữ nhật ABCD.A’B’C’D’ (Hình 2). Giá của vecto \(\overrightarrow {AA'} \) có vuông góc với mặt phẳng (ABCD) hay không?
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Quan sát hình vẽ ta thấy \(\overrightarrow {AA'} \) vuông góc với mặt phẳng (ABCD)
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 51 SGK Toán 12 Cánh diều
Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \)có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) và mặt phẳng (ABCD) (Hình 5)

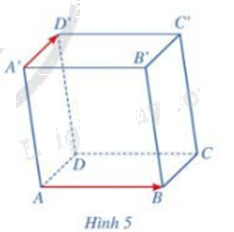
Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) và mặt phẳng (ABCD) (Hình 5)
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) không cùng phương
Giá của vecto \(\overrightarrow {AB} \) nằm trong mặt phẳng (ABCD)
Giá của vecto \(\overrightarrow {A'D'} \) song song với mặt phẳng (ABCD)
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 52 SGK Toán 12 Cánh diều
Cho cặp vecto chỉ phương \(\overrightarrow a = (1;0;1),\overrightarrow b = (2;1;0)\) của mặt phẳng (P).

a) Hãy chỉ ra tọa độ của một vecto \(\overrightarrow n (\overrightarrow n \ne \overrightarrow 0 )\) vuông góc với cả hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) (Hình 6)
b) Vecto \(\overrightarrow n \) có là vecto pháp tuyến của mặt phẳng (P) hay không?
Phương pháp giải:
a) Cho hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) không cùng phương. Khi đó, vecto \(\overrightarrow w = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \)
b) Cho mặt phẳng (P). Nếu vecto \(\overrightarrow n \) khác \(\overrightarrow 0 \) và có giá vuông góc với mặt phẳng (P) thì \(\overrightarrow n \) được gọi là vecto pháp tuyến của mặt phẳng ()
Lời giải chi tiết:
a) \(\overrightarrow n = (0.0 - 1.1;1.2 - 0.1;1.1 - 2.0) = ( - 1;2;1)\)
b) \(\overrightarrow n \) vuông góc với cả hai vecto chỉ phương của mặt phẳng (P) nên \(\overrightarrow n \) có giá vuông góc với mặt phẳng (P) và là vecto pháp tuyến của mặt phẳng (P)
- HĐ1
- HĐ2
- HĐ3
Trả lời câu hỏi Hoạt động 1 trang 50 SGK Toán 12 Cánh diều
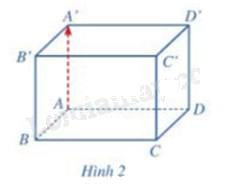
Cho hình hộp chữ nhật ABCD.A’B’C’D’ (Hình 2). Giá của vecto \(\overrightarrow {AA'} \) có vuông góc với mặt phẳng (ABCD) hay không?
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Quan sát hình vẽ ta thấy \(\overrightarrow {AA'} \) vuông góc với mặt phẳng (ABCD)
Trả lời câu hỏi Hoạt động 2 trang 51 SGK Toán 12 Cánh diều
Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \)có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) và mặt phẳng (ABCD) (Hình 5)

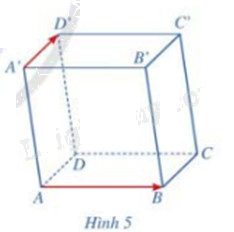
Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) và mặt phẳng (ABCD) (Hình 5)
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) không cùng phương
Giá của vecto \(\overrightarrow {AB} \) nằm trong mặt phẳng (ABCD)
Giá của vecto \(\overrightarrow {A'D'} \) song song với mặt phẳng (ABCD)
Trả lời câu hỏi Hoạt động 3 trang 52 SGK Toán 12 Cánh diều
Cho cặp vecto chỉ phương \(\overrightarrow a = (1;0;1),\overrightarrow b = (2;1;0)\) của mặt phẳng (P).
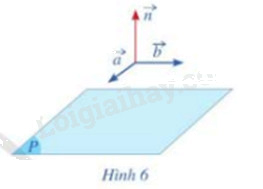
a) Hãy chỉ ra tọa độ của một vecto \(\overrightarrow n (\overrightarrow n \ne \overrightarrow 0 )\) vuông góc với cả hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) (Hình 6)
b) Vecto \(\overrightarrow n \) có là vecto pháp tuyến của mặt phẳng (P) hay không?
Phương pháp giải:
a) Cho hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) không cùng phương. Khi đó, vecto \(\overrightarrow w = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \)
b) Cho mặt phẳng (P). Nếu vecto \(\overrightarrow n \) khác \(\overrightarrow 0 \) và có giá vuông góc với mặt phẳng (P) thì \(\overrightarrow n \) được gọi là vecto pháp tuyến của mặt phẳng ()
Lời giải chi tiết:
a) \(\overrightarrow n = (0.0 - 1.1;1.2 - 0.1;1.1 - 2.0) = ( - 1;2;1)\)
b) \(\overrightarrow n \) vuông góc với cả hai vecto chỉ phương của mặt phẳng (P) nên \(\overrightarrow n \) có giá vuông góc với mặt phẳng (P) và là vecto pháp tuyến của mặt phẳng (P)
Giải mục 1 trang 50, 51, 52 SGK Toán 12 tập 2 - Cánh diều: Tổng quan và Hướng dẫn chi tiết
Mục 1 trang 50, 51, 52 SGK Toán 12 tập 2 Cánh diều là một phần quan trọng trong chương trình học tích phân của học sinh lớp 12. Nội dung tập trung vào việc vận dụng các kiến thức về tích phân để giải quyết các bài toán thực tế, đặc biệt là trong lĩnh vực tính diện tích hình phẳng.
Nội dung chính của Mục 1
- Bài tập 1: Tính tích phân xác định của một hàm số đơn giản.
- Bài tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành.
- Bài tập 3: Tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số.
- Bài tập 4: Ứng dụng tích phân để tính thể tích khối tròn xoay.
Hướng dẫn giải chi tiết từng bài tập
Để giúp các em học sinh hiểu rõ hơn về cách giải các bài tập trong mục này, Tusach.vn xin trình bày hướng dẫn chi tiết cho từng bài tập:
Bài tập 1: Tính tích phân xác định
Để tính tích phân xác định ∫ab f(x) dx, ta thực hiện các bước sau:
- Tìm nguyên hàm F(x) của hàm số f(x), tức là F'(x) = f(x).
- Tính giá trị của nguyên hàm tại cận trên và cận dưới: F(b) và F(a).
- Tính hiệu F(b) - F(a) để được kết quả của tích phân xác định.
Bài tập 2: Tính diện tích hình phẳng
Để tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và trục hoành trên đoạn [a, b], ta sử dụng công thức:
S = ∫ab |f(x)| dx
Trong đó, |f(x)| là giá trị tuyệt đối của hàm số f(x).
Bài tập 3: Tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
Để tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y = f(x) và y = g(x) trên đoạn [a, b], ta sử dụng công thức:
S = ∫ab |f(x) - g(x)| dx
Bài tập 4: Ứng dụng tích phân để tính thể tích khối tròn xoay
Có hai phương pháp chính để tính thể tích khối tròn xoay:
- Phương pháp đĩa: V = π∫ab [f(x)]2 dx
- Phương pháp vỏ: V = 2π∫ab x|f(x)| dx
Lưu ý khi giải bài tập
Khi giải các bài tập về tích phân, các em cần lưu ý những điều sau:
- Xác định đúng cận tích phân.
- Chọn phương pháp tích phân phù hợp.
- Kiểm tra lại kết quả sau khi tính toán.
Tusach.vn – Đồng hành cùng học sinh
Tusach.vn hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 50, 51, 52 SGK Toán 12 tập 2 Cánh diều. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.
| Bài tập | Nội dung | Lời giải |
|---|---|---|
| Bài tập 1 | Tính tích phân xác định | Xem chi tiết tại Tusach.vn |
| Bài tập 2 | Tính diện tích hình phẳng | Xem chi tiết tại Tusach.vn |