Giải mục 4 trang 57,58,59 SGK Toán 12 tập 2 - Cánh Diều

Giải mục 4 trang 57,58,59 SGK Toán 12 tập 2 - Cánh diều

Giải mục 4 trang 57,58,59 SGK Toán 12 tập 2 - Cánh Diều

Chào mừng các em học sinh đến với lời giải chi tiết mục 4 trang 57, 58, 59 SGK Toán 12 tập 2 - Cánh Diều trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.

Với mục tiêu hỗ trợ tối đa cho các em trong quá trình học tập, tusach.vn đã biên soạn và trình bày lời giải bài tập một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng.

Điều kiện song song, vuông góc của hai mặt phẳng

HĐ9

Trả lời câu hỏi Hoạt động 9 trang 58 SGK Toán 12 Cánh diều

Cho mặt phẳng \(({P_1})\) có phương trình tổng quát là \(x + 2y + z + 1 = 0\) và mặt phẳng \(({P_2})\) có phương trình tổng quát là \(3x - 2y + z + 5 = 0\)

Gọi \(\overrightarrow {{n_1}} = (1;2;1),\overrightarrow {{n_2}} = (3; - 2;1)\) lần lượt là vecto pháp tuyến của hai mặt phẳng \(({P_1}),({P_2})\) (Hình 14). Hai vecto \(\overrightarrow {{n_1}} \),\(\overrightarrow {{n_2}} \) có vuông góc với nhau hay không?

Phương pháp giải:

\(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \Leftrightarrow \overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0\)

Lời giải chi tiết:

\(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.3 + 2.( - 2) + 1.1 = 0\) suy ra \(\overrightarrow {{n_1}} \),\(\overrightarrow {{n_2}} \) vuông góc với nhau

Lựa chọn câu để xem lời giải nhanh hơn

HĐ8
HĐ9

Trả lời câu hỏi Hoạt động 8 trang 57 SGK Toán 12 Cánh diều

Cho mặt phẳng \(({P_1}):2x + 2y + 2z + 1 = 0\) (1) và mặt phẳng \(({P_2}):x + y + z - 1 = 0\) (2).

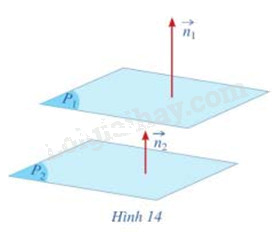
Giải mục 4 trang 57,58,59 SGK Toán 12 tập 2 - Cánh diều 1

a) Gọi \(\overrightarrow {{n_1}} = (2;2;2),\overrightarrow {{n_2}} = (1;1;1)\) lần lượt là vecto pháp tuyến của hai mặt phẳng \(({P_1}),({P_2})\) (Hình 14). Tìm liên hệ giữa \(\overrightarrow {{n_1}} \) và \(2\overrightarrow {{n_2}} \)

b) Tìm các hệ số tự do \({D_1},{D_2}\) lần lượt trong hai phương trình (1), (2). So sánh \({D_1}\) và \(2{D_2}\)

c) Nêu vị trí tương đối của hai mặt phẳng \(({P_1}),({P_2})\)

Phương pháp giải:

a), (b) Xác định \(\overrightarrow {{n_1}} \) và \(2\overrightarrow {{n_2}} \), \({D_1}\) và \(2{D_2}\) rồi so sánh

b) Quan sát hình vẽ

Lời giải chi tiết:

a) \(\;\overrightarrow {{n_1}} = 2\overrightarrow {{n_2}} = (2;2;2)\)

b) \({D_1}\)= 1; \(2{D_2}\) = -2

Vậy \({D_1} \ne 2{D_2}\)

c) \(({P_1})//({P_2})\)

Trả lời câu hỏi Hoạt động 9 trang 58 SGK Toán 12 Cánh diều

Cho mặt phẳng \(({P_1})\) có phương trình tổng quát là \(x + 2y + z + 1 = 0\) và mặt phẳng \(({P_2})\) có phương trình tổng quát là \(3x - 2y + z + 5 = 0\)

Phương pháp giải:

\(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \Leftrightarrow \overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0\)

Lời giải chi tiết:

\(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.3 + 2.( - 2) + 1.1 = 0\) suy ra \(\overrightarrow {{n_1}} \),\(\overrightarrow {{n_2}} \) vuông góc với nhau

HĐ8

Trả lời câu hỏi Hoạt động 8 trang 57 SGK Toán 12 Cánh diều

Cho mặt phẳng \(({P_1}):2x + 2y + 2z + 1 = 0\) (1) và mặt phẳng \(({P_2}):x + y + z - 1 = 0\) (2).

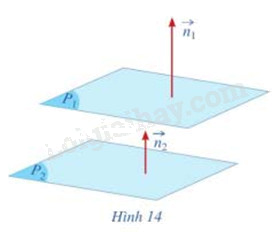
Giải mục 4 trang 57,58,59 SGK Toán 12 tập 2 - Cánh diều 0 1

b) Tìm các hệ số tự do \({D_1},{D_2}\) lần lượt trong hai phương trình (1), (2). So sánh \({D_1}\) và \(2{D_2}\)

c) Nêu vị trí tương đối của hai mặt phẳng \(({P_1}),({P_2})\)

Phương pháp giải:

a), (b) Xác định \(\overrightarrow {{n_1}} \) và \(2\overrightarrow {{n_2}} \), \({D_1}\) và \(2{D_2}\) rồi so sánh

b) Quan sát hình vẽ

Lời giải chi tiết:

a) \(\;\overrightarrow {{n_1}} = 2\overrightarrow {{n_2}} = (2;2;2)\)

b) \({D_1}\)= 1; \(2{D_2}\) = -2

Vậy \({D_1} \ne 2{D_2}\)

c) \(({P_1})//({P_2})\)

Giải mục 4 trang 57,58,59 SGK Toán 12 tập 2 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết

Mục 4 trong SGK Toán 12 tập 2 - Cánh Diều tập trung vào chủ đề về Đường thẳng và mặt phẳng trong không gian. Đây là một phần kiến thức quan trọng, nền tảng cho việc học tập các chương tiếp theo và cũng thường xuyên xuất hiện trong các kỳ thi quan trọng như THPT Quốc gia. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập liên quan đến đường thẳng và mặt phẳng là điều cần thiết để đạt kết quả tốt môn Toán.

Nội dung chính của Mục 4

Vị trí tương đối của hai đường thẳng trong không gian: Song song, cắt nhau, chéo nhau.
Góc giữa hai đường thẳng trong không gian: Cách tính góc, ứng dụng trong giải bài tập.
Vị trí tương đối của đường thẳng và mặt phẳng trong không gian: Nằm trong mặt phẳng, song song với mặt phẳng, cắt mặt phẳng.
Góc giữa đường thẳng và mặt phẳng trong không gian: Cách tính góc, ứng dụng trong giải bài tập.
Khoảng cách từ một điểm đến mặt phẳng: Công thức tính khoảng cách, ứng dụng trong giải bài tập.

Giải chi tiết các bài tập trang 57, 58, 59

Dưới đây là lời giải chi tiết cho từng bài tập trong mục 4 trang 57, 58, 59 SGK Toán 12 tập 2 - Cánh Diều: