Giải bài tập 14 trang 89 SGK Toán 12 tập 2 - Cánh diều
Tổng quan nội dung
Giải Bài Tập 14 Trang 89 Toán 12 Tập 2 - Cánh Diều
Chào mừng bạn đến với lời giải chi tiết bài tập 14 trang 89 SGK Toán 12 tập 2 - Cánh Diều trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp bạn hiểu sâu sắc kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất cho học sinh.
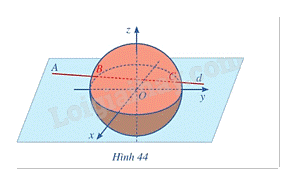
Trong không gian với hệ toạ độ Oxyz, đài kiểm soát không lưu sân bay có toạ độ O(0; 0; 0), mỗi đơn vị trên trục ứng với 1 km. Máy bay bay trong phạm vi cách đài kiểm soát 417km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A(– 688; – 185; 8), chuyển động theo đường thẳng d có vectơ chỉ phương là (overrightarrow u = left( {91;75;0} right)) hướng về đài kiểm soát không lưu (Hình 44).
Đề bài
Trong không gian với hệ toạ độ Oxyz, đài kiểm soát không lưu sân bay có toạ độ O(0; 0; 0), mỗi đơn vị trên trục ứng với 1 km. Máy bay bay trong phạm vi cách đài kiểm soát 417km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A(– 688; – 185; 8), chuyển động theo đường thẳng d có vectơ chỉ phương là \(\overrightarrow u = \left( {91;75;0} \right)\) hướng về đài kiểm soát không lưu (Hình 44).
a) Xác định toạ độ của vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
b) Xác định toạ độ của vị trí mà máy bay bay gần đài kiểm soát không lưu nhất. Tính khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó.
c) Xác định toạ độ của vị trí mà máy bay ra khỏi màn hình ra đa.
Phương pháp giải - Xem chi tiết
a) + Viết phương trình đường thẳng d đi qua điểm A và có một vectơ chỉ phương \(\overrightarrow u \).
+ Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa. B thuộc d nên tính tọa độ của B theo t.
+ B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa thì \(OB = 417\). Từ đó có phương trình theo ẩn t, giải phương trình tính t.
+ Thay giá trị t tính được để tìm tọa độ B, so sánh giá trị và được ra kết luận.
b) + Gọi H là vị trí mà máy bay gần đài kiểm soát không lưu nhất.
+ Vì H thuộc d nên tính tọa độ của H theo t’.
+ OH ngắn nhất khi và chỉ khi \(OH \bot d \Leftrightarrow \overrightarrow {OH} \bot \overrightarrow u \Leftrightarrow \overrightarrow {OH} .\overrightarrow u = 0\), từ đó tính được t’.
+ Từ đó tính được H và khoảng cách OH cần tìm.
Lời giải chi tiết
a) Đường thẳng d đi qua điểm A(-688;-185;8), có một vectơ chỉ phương \(\overrightarrow u = \left( {91;75;0} \right)\) có phương trình tham số là: \(\left\{ \begin{array}{l}x = - 688 + 91t\\y = - 185 + 75t\\z = 8\end{array} \right.\) (t là tham số).
Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
Vì B thuộc d nên B(-688 + 91t; -185 + 75t; 8).
Để B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa thì \(OB = 417\).
Do đó, \(\sqrt {{{\left( { - 688 + 91t} \right)}^2} + {{\left( { - 185 + 75t} \right)}^2} + {8^2}} = 417\)
\( \Leftrightarrow 13\;906{t^2} - 152\;966t + 333\;744 = 0\)\( \Leftrightarrow t = 3\) hoặc \(t = 8\).
Với \(t = 3\) ta có B(-415; 40; 8) và \(AB = \sqrt {{{\left( { - 415 + 688} \right)}^2} + {{\left( {40 + 185} \right)}^2}} = \sqrt {125\;154} \).
Với \(t = 8\) ta có B(40; 415; 8) và \(AB = \sqrt {{{\left( {40 + 688} \right)}^2} + {{\left( {415 + 185} \right)}^2}} = \sqrt {889\;984} \).
Vì \(\sqrt {125\;154} < \sqrt {889\;984} \) nên tọa độ vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa là (-415; 40; 8).
b) Gọi H là vị trí mà máy bay gần đài kiểm soát không lưu nhất. Vì H thuộc d nên H(-688+91t’; -185+75t’;8).
Để OH là ngắn nhất khi và chỉ khi \(OH \bot d \Leftrightarrow \overrightarrow {OH} \bot \overrightarrow u \Leftrightarrow \overrightarrow {OH} .\overrightarrow u = 0\)
\( \Leftrightarrow \left( { - 688 + 91t'} \right).91 + \left( { - 185 + 75t'} \right).75 + 8.0 = 0 \Leftrightarrow 13\;906t' - 76\;483 = 0 \Leftrightarrow t' = \frac{{11}}{2}\).
Do đó, \(H\left( {\frac{{ - 375}}{2};\frac{{455}}{2};8} \right)\).
Khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó là:
\(OH = \sqrt {{{\left( {\frac{{ - 375}}{2}} \right)}^2} + {{\left( {\frac{{455}}{2}} \right)}^2} + {8^2}} = \frac{{\sqrt {347\;906} }}{2}\left( {km} \right)\).
c) Theo a ta có: tọa độ của vị trí mà máy bay ra khỏi màn hình ra đa là: (40; 415; 8).
Giải Bài Tập 14 Trang 89 Toán 12 Tập 2 - Cánh Diều: Hướng Dẫn Chi Tiết
Bài tập 14 trang 89 SGK Toán 12 tập 2 - Cánh Diều thuộc chương trình học về Đường Thẳng và Mặt Phẳng trong Không Gian. Đây là một bài tập quan trọng, giúp học sinh rèn luyện kỹ năng về việc xác định vị trí tương đối giữa đường thẳng và mặt phẳng, cũng như ứng dụng các công thức tính khoảng cách.
Nội Dung Bài Tập 14
Bài tập 14 thường yêu cầu học sinh:
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng (song song, nằm trong mặt phẳng, cắt nhau).
- Tính khoảng cách từ một điểm đến một mặt phẳng.
- Tính góc giữa đường thẳng và mặt phẳng.
- Giải các bài toán thực tế liên quan đến ứng dụng của đường thẳng và mặt phẳng.
Lời Giải Chi Tiết Bài Tập 14 (Ví dụ)
Để minh họa, chúng ta sẽ cùng giải một ví dụ cụ thể. Giả sử bài tập yêu cầu:
Cho điểm A(1; 2; 3) và mặt phẳng (P): 2x - y + z - 1 = 0. Tính khoảng cách từ điểm A đến mặt phẳng (P).
Lời giải:
- Công thức tính khoảng cách: Khoảng cách d từ điểm A(x0; y0; z0) đến mặt phẳng (P): Ax + By + Cz + D = 0 được tính theo công thức:
- d = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2)
- Áp dụng công thức: Trong trường hợp này, ta có A = 2, B = -1, C = 1, D = -1, x0 = 1, y0 = 2, z0 = 3.
- d = |2(1) - 1(2) + 1(3) - 1| / √(22 + (-1)2 + 12)
- d = |2 - 2 + 3 - 1| / √(4 + 1 + 1)
- d = 2 / √6 = √6 / 3
Vậy, khoảng cách từ điểm A đến mặt phẳng (P) là √6 / 3.
Mẹo Giải Bài Tập Hiệu Quả
- Nắm vững lý thuyết: Hiểu rõ các định nghĩa, định lý và công thức liên quan đến đường thẳng và mặt phẳng.
- Vẽ hình minh họa: Vẽ hình giúp bạn hình dung rõ hơn về bài toán và tìm ra phương pháp giải phù hợp.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng tài liệu tham khảo: Tham khảo sách giáo khoa, sách bài tập, các trang web học tập uy tín để tìm kiếm thêm kiến thức và lời giải.
Tại Sao Nên Chọn tusach.vn?
tusach.vn là địa chỉ tin cậy cho học sinh, sinh viên tìm kiếm lời giải bài tập Toán. Chúng tôi cung cấp:
- Lời giải chi tiết, dễ hiểu, được trình bày rõ ràng.
- Đội ngũ giáo viên giàu kinh nghiệm, chuyên môn cao.
- Cập nhật liên tục các bài giải mới nhất.
- Giao diện thân thiện, dễ sử dụng.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Bảng Tổng Hợp Các Công Thức Quan Trọng
| Công Thức | Mô Tả |
|---|---|
| Khoảng cách từ điểm A đến mặt phẳng (P) | d = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2) |
| Góc giữa đường thẳng d và mặt phẳng (P) | sin φ = |a1A + a2B + a3C| / √(a12 + a22 + a32)√(A2 + B2 + C2) |
Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!