Giải bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều
Tổng quan nội dung
Giải bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều
Bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học Toán 12, tập trung vào việc rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ bản chất và phương pháp giải, từ đó tự tin hơn trong các bài kiểm tra và thi cử.
Khảo sát sự biến thiên của các hàm số sau: a, \(y = \frac{{x - 1}}{{x + 1}}\) b,\(y = \frac{{ - 2x}}{{x + 1}}\) c,\(y=\frac{{{x^2} - 3x + 6}}{{x - 1}}\) d,\(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\) e,\(y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}\) g,\(y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}\)
Đề bài
Khảo sát sự biến thiên của các hàm số sau:
a, \(y = \frac{{x - 1}}{{x + 1}}\)
b,\(y = \frac{{ - 2x}}{{x + 1}}\)
c,\(y=\frac{{{x^2} - 3x + 6}}{{x - 1}}\)
d,\(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)
e,\(y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}\)
g,\(y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}\)
Lời giải chi tiết
a) \(y = \frac{{x - 1}}{{x + 1}}\)
1) TXĐ: \(x \in \mathbb{R}\left\{ { - 1} \right\}\)
2) Sự biến thiên
\(y' = \frac{2}{{{{\left( {x + 1} \right)}^2}}} > 0\;\) với mọi \(x \ne - 1\)
Bảng biến thiên:
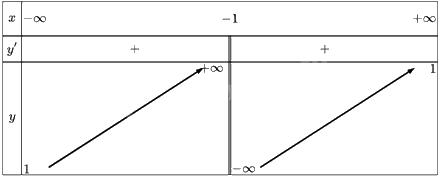
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\)
Hàm số không có cực trị
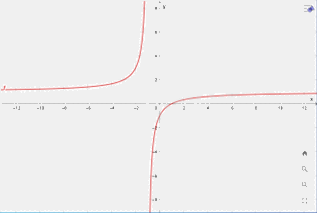
3) Đồ thị
Giao điểm đồ thị với trục tung: \(\left( {0; - 1} \right)\)
Giao điểm đồ thị với trục hoành: \(\left( {1;0} \right)\)
Đồ thị đi qua các điểm: \(\left( {0; - 1} \right)\), \(\left( {1;0} \right)\)
b) \(y = \frac{{ - 2x}}{{x + 1}}\)
1) TXĐ: \(x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\)
2) Sự biến thiên
với mọi \(x \ne - 1\)
Bảng biến thiên:
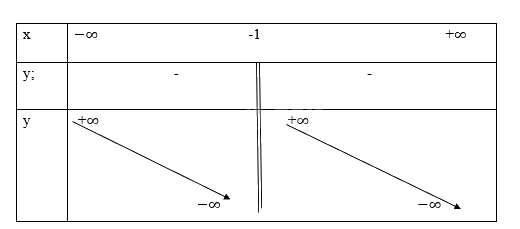
Hàm số nghịch biến trên khoảng \(\left( { - \infty , - 1} \right) \cup \left( { - 1,\infty } \right)\)
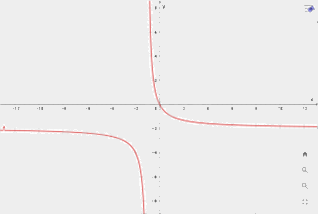
3) Đồ thị
Giao điểm đồ thị với trục tung: \(\left( {0;0} \right)\)
Giao điểm đồ thị với trục hoành: \(\left( {0;0} \right)\)
c) \(y = \frac{{{x^2} - 3x + 6}}{{x - 1}}\)
1) TXĐ: \(x \in \mathbb{R}\backslash \left\{ 1 \right\}\)
2) Sự biến thiên
Ta có \(y = \frac{{{x^2} - 3x + 6}}{{x - 1}}\)\( = x - 2 + \frac{4}{{x - 1}}\)
\(y' = 1 - \frac{4}{{{{(x - 1)}^2}}}\)\( = \frac{{{x^2} - 2x - 3}}{{{{(x - 1)}^2}}}\)
Xét \(y' = 0\)\( \Rightarrow \left[ \begin{array}{l}x = 3\\x = - 1\end{array} \right.\)
Bảng biến thiên
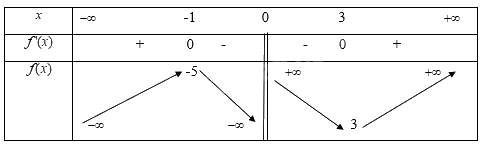
Hàm số đồng biến trên khoảng \(\left( { - \infty , - 1} \right),\left( {3, + \infty } \right)\). Nghịch biến trên khoảng \(\left( { - 1,1} \right),\left( {1,3} \right)\)
3) Đồ thị
Giao điểm đồ thị với trục tung: \(\left( {0; - 6} \right)\)
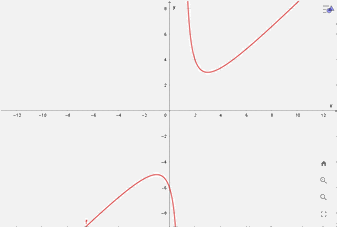
d) \(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)
Hàm số trên xác định trên R\{2}
Ta có \(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)\( = - x - \frac{4}{{x - 2}}\)
\(y' = - 1 + \frac{4}{{{{(x - 2)}^2}}}\)\( = \frac{{ - {x^2} + 4x}}{{{{(x - 2)}^2}}}\)
Xét \(y' = 0\)\( \Rightarrow \left[ \begin{array}{l}x = 0\\x = 4\end{array} \right.\)
Từ đó ta có bảng biến thiên là

Từ bảng biến thiên ta thấy
Hàm số đồng biến \(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)trên các khoảng \((0;2)\) và \((2;4)\)
Hàm số nghịch biến \(y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}\)trên các khoảng \(( - \infty ;0)\) và \((4; + \infty )\)
Ta có đồ thị hàm số là
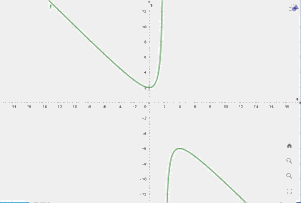
e) \(y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}\)
Hàm số xác định trên R\{-2}
Ta có \(y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}\) \( = 2x - \frac{{x + 5}}{{x + 2}}\)
\(y' = 2 + \frac{3}{{{{(x + 2)}^2}}}\)
Vì \(y' > 0\)với \(x \in R/\left\{ { - 2} \right\}\)
Nên hàm số luôn đồng biến với \(x \in R/\left\{ { - 2} \right\}\)
Ta có đồ thị hàm số là

g) \(y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}\)
Hàm số xác định trên R/{2}
Ta có : \(y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}\) \( = - x + \frac{3}{{x - 2}}\)
\(y' = - 1 - \frac{3}{{{{(x - 2)}^2}}}\)
Vì \(y' < 0\)với \(x \in R/\left\{ 2 \right\}\)
Nên hàm số luôn nghịch biến với \(x \in R/\left\{ 2 \right\}\)
Ta có đồ thị hàm số là

Giải bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều: Hướng dẫn chi tiết và dễ hiểu
Bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế liên quan đến việc tìm đạo hàm và khảo sát hàm số.
Nội dung bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều
Bài tập 6 thường có dạng như sau: Cho hàm số y = f(x). Hãy tìm đạo hàm f'(x) và sử dụng đạo hàm để khảo sát hàm số (xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn,...).
Phương pháp giải bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều
- Bước 1: Tính đạo hàm f'(x): Sử dụng các quy tắc tính đạo hàm đã học (đạo hàm của tổng, hiệu, tích, thương, hàm hợp,...).
- Bước 2: Tìm tập xác định của hàm số: Xác định các giá trị của x mà hàm số có nghĩa.
- Bước 3: Tìm các điểm tới hạn: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0.
- Bước 4: Lập bảng biến thiên: Dựa vào dấu của f'(x) trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến của hàm số.
- Bước 5: Xác định cực trị: Sử dụng dấu của f'(x) để xác định các điểm cực đại, cực tiểu của hàm số.
- Bước 6: Tìm điểm uốn (nếu có): Tính đạo hàm cấp hai f''(x) và giải phương trình f''(x) = 0 để tìm các điểm uốn.
Ví dụ minh họa giải bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Hãy khảo sát hàm số.
Giải:
- Bước 1: Tính đạo hàm: y' = 3x2 - 6x
- Bước 2: Tập xác định: D = R
- Bước 3: Tìm điểm tới hạn: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Bước 4: Lập bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | NB | ĐB | NB |
Kết luận: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.
Lưu ý khi giải bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều
- Nắm vững các quy tắc tính đạo hàm.
- Chú ý xác định đúng tập xác định của hàm số.
- Lập bảng biến thiên một cách chính xác.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều. Chúc các em học tốt!