Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải mục 2 trang 34,35,36 SGK Toán 12 tập 2 - Cánh diều
SGK Toán 12 - Cánh diều
Giải Toán 12 tập 2 - Cánh diều
Chương 4. Nguyên hàm. Tích phân
Bài 4. Ứng dụng hình học của tích phân

Giải mục 2 trang 34,35,36 SGK Toán 12 tập 2 - Cánh diều

Giải mục 2 trang 34,35,36 SGK Toán 12 tập 2 - Cánh Diều

Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 34, 35, 36 SGK Toán 12 tập 2 chương trình Cánh Diều. Bài viết này sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập trong chương trình học.

tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những tài liệu và lời giải chính xác, dễ hiểu nhất.

Tính thể tích của hình khối

HĐ3HĐ4

HĐ3

    Trả lời câu hỏi Hoạt động 3 trang 34 SGK Toán 12 Cánh diều

    Cắt khối lập phương có cạnh bằng 1 bởi một mặt phẳng tùy ý vuông góc với trục Ox tại x, với ta nhận được hình phẳng có diện tích là S(x) (Hình 17)

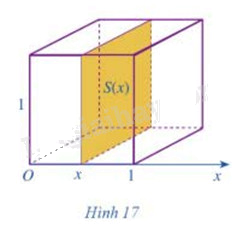
    Giải mục 2 trang 34,35,36 SGK Toán 12 tập 2 - Cánh diều 0 1

    a) Tính S(x)

    b) So sánh thể tích khối lập phương đó với \(\int\limits_0^1 {S(x)dx} \)

    Phương pháp giải:

    Sử dụng công thức tính diện tích hình vuông, thể tích hình lập phương và tích phân

    Lời giải chi tiết:

    a) S(x) = 1

    b) Thể tích khối lập phương V = 1

    \(\int\limits_0^1 {S(x)dx} = \int\limits_0^1 {1dx} = 1\)

    Vậy thể tích khối lập phương đó = \(\int\limits_0^1 {S(x)dx} \)

    Lựa chọn câu để xem lời giải nhanh hơn
    • HĐ3
    • HĐ4

    Trả lời câu hỏi Hoạt động 3 trang 34 SGK Toán 12 Cánh diều

    Cắt khối lập phương có cạnh bằng 1 bởi một mặt phẳng tùy ý vuông góc với trục Ox tại x, với ta nhận được hình phẳng có diện tích là S(x) (Hình 17)

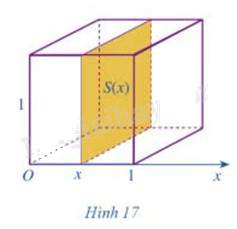
    Giải mục 2 trang 34,35,36 SGK Toán 12 tập 2 - Cánh diều 1

    a) Tính S(x)

    b) So sánh thể tích khối lập phương đó với \(\int\limits_0^1 {S(x)dx} \)

    Phương pháp giải:

    Sử dụng công thức tính diện tích hình vuông, thể tích hình lập phương và tích phân

    Lời giải chi tiết:

    a) S(x) = 1

    b) Thể tích khối lập phương V = 1

    \(\int\limits_0^1 {S(x)dx} = \int\limits_0^1 {1dx} = 1\)

    Vậy thể tích khối lập phương đó = \(\int\limits_0^1 {S(x)dx} \)

    Trả lời câu hỏi Hoạt động 4 trang 37 SGK Toán 12 Cánh diều

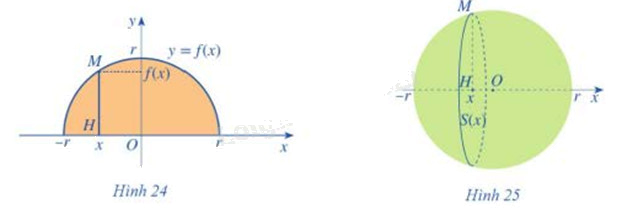
    Xét hình tròn tâm O, bán kính r (Hình 24). Nửa hình tròn đó là hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y = f(x)

    a) Tìm hàm số y = f(x)

    b) Quay nửa hình tròn đó quanh trục hoành, ta nhận được hình cầu tâm O bán kính r (Hình 25). Xét điểm M(x;f(x)) \(( - r \le x \le r)\) nằm trên nửa đường tròn tâm O bán kính r. Gọi H(x;0) là hình chiếu của điểm M trên trục Ox. Khi quay nửa hình tròn quanh trục hoành, đoạn thẳng HM tạo nên một hình tròn tâm H bán kính f(x)

    Tính diện tích S(x) của hình tròn đó theo f(x)

    Từ đó, sử dụng công thức tính thể tích vật thể, hãy tính thể tích V của hình cầu tâm O bán kính r

    Giải mục 2 trang 34,35,36 SGK Toán 12 tập 2 - Cánh diều 2

    Phương pháp giải:

    a) Tìm hàm số y = f(x) thông qua phương trình nửa đường tròn

    b) Sử dụng công thức tính thể tích hình cầu

    Lời giải chi tiết:

    a) Hàm số y = f(x) chính là phương trình của nửa đường tròn có tâm O, bán kính r

    \( \Rightarrow y = f(x) = \sqrt {{r^2} - {x^2}} \)

    b) \(S(x) = \pi {f^2}(x)\)

    \(V = \frac{{4\pi {r^3}}}{3}\)

    HĐ4

      Trả lời câu hỏi Hoạt động 4 trang 37 SGK Toán 12 Cánh diều

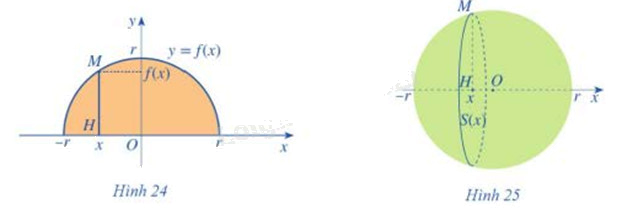
      Xét hình tròn tâm O, bán kính r (Hình 24). Nửa hình tròn đó là hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y = f(x)

      a) Tìm hàm số y = f(x)

      b) Quay nửa hình tròn đó quanh trục hoành, ta nhận được hình cầu tâm O bán kính r (Hình 25). Xét điểm M(x;f(x)) \(( - r \le x \le r)\) nằm trên nửa đường tròn tâm O bán kính r. Gọi H(x;0) là hình chiếu của điểm M trên trục Ox. Khi quay nửa hình tròn quanh trục hoành, đoạn thẳng HM tạo nên một hình tròn tâm H bán kính f(x)

      Tính diện tích S(x) của hình tròn đó theo f(x)

      Từ đó, sử dụng công thức tính thể tích vật thể, hãy tính thể tích V của hình cầu tâm O bán kính r

      Giải mục 2 trang 34,35,36 SGK Toán 12 tập 2 - Cánh diều 1 1

      Phương pháp giải:

      a) Tìm hàm số y = f(x) thông qua phương trình nửa đường tròn

      b) Sử dụng công thức tính thể tích hình cầu

      Lời giải chi tiết:

      a) Hàm số y = f(x) chính là phương trình của nửa đường tròn có tâm O, bán kính r

      \( \Rightarrow y = f(x) = \sqrt {{r^2} - {x^2}} \)

      b) \(S(x) = \pi {f^2}(x)\)

      \(V = \frac{{4\pi {r^3}}}{3}\)

      Giải mục 2 trang 34,35,36 SGK Toán 12 tập 2 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết

      Mục 2 trong SGK Toán 12 tập 2 Cánh Diều thường xoay quanh các chủ đề về đạo hàm của hàm số, ứng dụng của đạo hàm trong việc khảo sát hàm số và tìm cực trị. Việc nắm vững kiến thức này là vô cùng quan trọng để giải quyết các bài toán liên quan đến hàm số, đặc biệt là trong các kỳ thi quan trọng như THPT Quốc gia.

      Nội dung chính của Mục 2 trang 34,35,36

      • Đạo hàm của hàm số hợp: Ôn lại quy tắc tính đạo hàm của hàm hợp, một công cụ quan trọng để giải quyết các bài toán phức tạp.
      • Đạo hàm của hàm ẩn: Tìm hiểu cách tính đạo hàm của hàm số được xác định một cách ẩn, thường gặp trong các bài toán liên quan đến đường cong.
      • Ứng dụng của đạo hàm để khảo sát hàm số: Sử dụng đạo hàm để xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn của hàm số.
      • Bài tập thực hành: Giải các bài tập cụ thể để củng cố kiến thức và rèn luyện kỹ năng giải toán.

      Hướng dẫn giải chi tiết các bài tập trong Mục 2

      Dưới đây là hướng dẫn giải chi tiết các bài tập trong Mục 2 trang 34, 35, 36 SGK Toán 12 tập 2 Cánh Diều:

      Bài 1: Tính đạo hàm của các hàm số sau

      Để giải bài tập này, các em cần áp dụng quy tắc tính đạo hàm của hàm hợp và các quy tắc đạo hàm cơ bản. Ví dụ:

      Nếu y = f(u) và u = g(x) thì dy/dx = (dy/du) * (du/dx)

      Bài 2: Tìm đạo hàm của hàm số y = x2 + 2x - 1

      Áp dụng quy tắc đạo hàm của hàm số đa thức, ta có:

      dy/dx = 2x + 2

      Bài 3: Khảo sát hàm số y = x3 - 3x + 2

      Để khảo sát hàm số, các em cần thực hiện các bước sau:

      1. Tính đạo hàm bậc nhất: y' = 3x2 - 3
      2. Tìm điểm cực trị: Giải phương trình y' = 0 để tìm các điểm cực trị.
      3. Xác định khoảng đồng biến, nghịch biến: Dựa vào dấu của đạo hàm bậc nhất để xác định khoảng đồng biến và nghịch biến của hàm số.
      4. Tính đạo hàm bậc hai: y'' = 6x
      5. Tìm điểm uốn: Giải phương trình y'' = 0 để tìm các điểm uốn.
      6. Vẽ đồ thị hàm số: Dựa vào các thông tin đã tìm được để vẽ đồ thị hàm số.

      Mẹo giải nhanh và hiệu quả

      • Nắm vững các quy tắc đạo hàm cơ bản: Điều này sẽ giúp các em giải quyết các bài toán một cách nhanh chóng và chính xác.
      • Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải toán.
      • Sử dụng các công cụ hỗ trợ: Các công cụ tính đạo hàm trực tuyến có thể giúp các em kiểm tra lại kết quả của mình.

      Tài liệu tham khảo thêm

      Ngoài SGK Toán 12 tập 2 Cánh Diều, các em có thể tham khảo thêm các tài liệu sau:

      • Sách bài tập Toán 12
      • Các trang web học toán trực tuyến
      • Các video hướng dẫn giải toán trên YouTube

      Hy vọng bài viết này sẽ giúp các em giải quyết thành công các bài tập trong Mục 2 trang 34, 35, 36 SGK Toán 12 tập 2 Cánh Diều. Chúc các em học tập tốt!

      Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

      CHỦ ĐỀ SÁCH XEM NHIỀU

      Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

      VỀ TUSACH.VN