Giải mục 2 trang 69, 70, 71 SGK Toán 12 tập 2 - Cánh diều
Tổng quan nội dung
Giải mục 2 trang 69, 70, 71 SGK Toán 12 tập 2 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 69, 70, 71 SGK Toán 12 tập 2 - Cánh Diều. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em hiểu rõ kiến thức và tự tin giải quyết các bài toán.
Bài tập trong mục này tập trung vào các kiến thức về... (điền kiến thức trọng tâm của mục 2). Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, kèm theo các lưu ý quan trọng để các em có thể nắm vững kiến thức.
Cho hai đường thẳng phân biệt \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({M_1},{M_2}\) và tương ứng có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) . a) Giả sử \({\Delta _1}\) song song với \({\Delta _2}\) (Hình 25). Các cặp vectơ sau có cùng phương hay không: \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \); \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \)?
LT5
Trả lời câu hỏi Luyện tập 5 trang 70 SGK Toán 12 Cánh diều
Bằng cách giải hệ phương trình, xác định vị trí tương đối của hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = {t_1}\\y = 1\\z = 0\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 2\\y = {t_2}\\z = 0\end{array} \right.\).
Phương pháp giải:
Sử dụng cách giải hệ phương trình chứa hai phương trình của hai đường thẳng, ta xác định vị trí tương đối của hai đường thẳng.
Lời giải chi tiết:
Xét hệ phương trình: \(\left\{ \begin{array}{l}{t_1} = 2\\1 = {t_2}\\0 = 0\end{array} \right.\). Hệ phương trình này có một nghiệm duy nhất nên hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
- HĐ5
- LT5
Trả lời câu hỏi Hoạt động 5 trang 69 SGK Toán 12 Cánh diều
Cho hai đường thẳng phân biệt \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({M_1},{M_2}\) và tương ứng có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) .
a) Giả sử \({\Delta _1}\) song song với \({\Delta _2}\) (Hình 25). Các cặp vectơ sau có cùng phương hay không: \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \); \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \)?
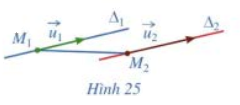
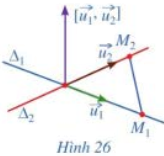
b) Giả sử \({\Delta _1}\) và \({\Delta _2}\) cắt nhau (Hình 26). Hai vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) có cùng phương hay không? Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) có đồng phẳng hay không?
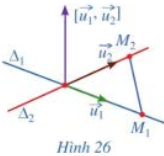
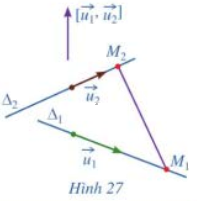
c) Giả sử \({\Delta _1}\) và \({\Delta _2}\) chéo nhau (Hình 27). Hai vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) có cùng phương hay không? Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) có đồng phẳng hay không?
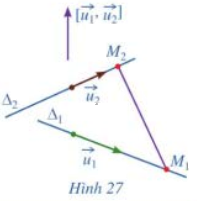
Phương pháp giải:
+ Sử dụng kiến thức về giá của vectơ trong không gian để trả lời: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ.
+ Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để trả lời: Cho đường thẳng \(\Delta \) và vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \) . Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).
Lời giải chi tiết:
a) Vì \({\Delta _1}\) song song với \({\Delta _2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) cùng phương.
Vì \({M_1}\) thuộc đường thẳng \({\Delta _1}\), \({M_2}\) thuộc đường thẳng \({\Delta _2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \) không cùng phương.
b) Vì \({\Delta _1}\) và \({\Delta _2}\) cắt nhau nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) đồng phẳng.
c) Vì \({\Delta _1}\) và \({\Delta _2}\) chéo nhau nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) không đồng phẳng.
Trả lời câu hỏi Luyện tập 5 trang 70 SGK Toán 12 Cánh diều
Bằng cách giải hệ phương trình, xác định vị trí tương đối của hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = {t_1}\\y = 1\\z = 0\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 2\\y = {t_2}\\z = 0\end{array} \right.\).
Phương pháp giải:
Sử dụng cách giải hệ phương trình chứa hai phương trình của hai đường thẳng, ta xác định vị trí tương đối của hai đường thẳng.
Lời giải chi tiết:
Xét hệ phương trình: \(\left\{ \begin{array}{l}{t_1} = 2\\1 = {t_2}\\0 = 0\end{array} \right.\). Hệ phương trình này có một nghiệm duy nhất nên hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 69 SGK Toán 12 Cánh diều
Cho hai đường thẳng phân biệt \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({M_1},{M_2}\) và tương ứng có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) .
a) Giả sử \({\Delta _1}\) song song với \({\Delta _2}\) (Hình 25). Các cặp vectơ sau có cùng phương hay không: \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \); \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \)?
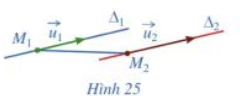
b) Giả sử \({\Delta _1}\) và \({\Delta _2}\) cắt nhau (Hình 26). Hai vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) có cùng phương hay không? Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) có đồng phẳng hay không?
c) Giả sử \({\Delta _1}\) và \({\Delta _2}\) chéo nhau (Hình 27). Hai vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) có cùng phương hay không? Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) có đồng phẳng hay không?
Phương pháp giải:
+ Sử dụng kiến thức về giá của vectơ trong không gian để trả lời: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ.
+ Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để trả lời: Cho đường thẳng \(\Delta \) và vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \) . Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).
Lời giải chi tiết:
a) Vì \({\Delta _1}\) song song với \({\Delta _2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) cùng phương.
Vì \({M_1}\) thuộc đường thẳng \({\Delta _1}\), \({M_2}\) thuộc đường thẳng \({\Delta _2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \) không cùng phương.
b) Vì \({\Delta _1}\) và \({\Delta _2}\) cắt nhau nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) đồng phẳng.
c) Vì \({\Delta _1}\) và \({\Delta _2}\) chéo nhau nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) không đồng phẳng.
Giải mục 2 trang 69, 70, 71 SGK Toán 12 tập 2 - Cánh Diều: Hướng dẫn chi tiết và dễ hiểu
Mục 2 của SGK Toán 12 tập 2 - Cánh Diều thường xoay quanh các kiến thức về (ví dụ: Đạo hàm của hàm số hợp, quy tắc tính đạo hàm). Việc nắm vững các kiến thức này là vô cùng quan trọng để giải quyết các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong các chương tiếp theo.
Nội dung chính của Mục 2
- Kiến thức lý thuyết: (Liệt kê các kiến thức lý thuyết chính của mục 2, ví dụ: Quy tắc đạo hàm của hàm hợp, đạo hàm của hàm lượng giác, đạo hàm của hàm mũ và logarit).
- Các dạng bài tập thường gặp: (Liệt kê các dạng bài tập thường gặp trong mục 2, ví dụ: Tính đạo hàm của hàm số phức tạp, tìm đạo hàm cấp hai, ứng dụng đạo hàm để giải các bài toán về cực trị).
- Phương pháp giải bài tập: (Mô tả các phương pháp giải bài tập hiệu quả cho từng dạng bài tập).
Giải chi tiết bài tập trang 69
Bài 1: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo các bước giải thích rõ ràng). Lưu ý: (Các lưu ý quan trọng khi giải bài tập này).
Bài 2: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo các bước giải thích rõ ràng). Lưu ý: (Các lưu ý quan trọng khi giải bài tập này).
Giải chi tiết bài tập trang 70
Bài 3: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo các bước giải thích rõ ràng). Lưu ý: (Các lưu ý quan trọng khi giải bài tập này).
Bài 4: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo các bước giải thích rõ ràng). Lưu ý: (Các lưu ý quan trọng khi giải bài tập này).
Giải chi tiết bài tập trang 71
Bài 5: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo các bước giải thích rõ ràng). Lưu ý: (Các lưu ý quan trọng khi giải bài tập này).
Bài 6: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo các bước giải thích rõ ràng). Lưu ý: (Các lưu ý quan trọng khi giải bài tập này).
Mẹo giải nhanh
Để giải nhanh các bài tập về đạo hàm, các em cần nắm vững các công thức đạo hàm cơ bản và các quy tắc tính đạo hàm. Ngoài ra, việc luyện tập thường xuyên cũng giúp các em làm quen với các dạng bài tập và rèn luyện kỹ năng giải toán.
Tổng kết
Hy vọng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 69, 70, 71 SGK Toán 12 tập 2 - Cánh Diều. Tusach.vn sẽ tiếp tục đồng hành cùng các em trên con đường chinh phục kiến thức.
| Bài tập | Trang | Độ khó |
|---|---|---|
| Bài 1 | 69 | Dễ |
| Bài 2 | 69 | Trung bình |
| Bài 3 | 70 | Trung bình |