Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều
SGK Toán 12 - Cánh diều
Giải Toán 12 tập 2 - Cánh diều
Chương 4. Nguyên hàm. Tích phân
Bài 2. Nguyên hàm của một số hàm số sơ cấp

Giải bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều

Giải bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều. Bài tập này thuộc chương trình học Toán 12, tập trung vào kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và các tài liệu học tập hữu ích khác.

Cây cà chua khi trồng có chiều cao 5cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng được cho bởi hàm số (v(t) = - 0,1{t^3} + {t^2}) Trong đó t tính theo tuần, v(t) tính bằng cm/tuần. Gọi h(t) (tính bằng cm) là độ cao của cây cà chua ở tuần thứ t a) Viết công thức xác định hàm số h(t) ((t ge 0)) b) Giai đoạn tăng trưởng của cây cà chua đó kéo dài bao lâu? c) Chiều cao tối đa của cây cà chua đó là bao nhiêu? d) Vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua

Đề bài

Cây cà chua khi trồng có chiều cao 5cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng được cho bởi hàm số

\(v(t) = - 0,1{t^3} + {t^2}\)

trong đó t tính theo tuần, v(t) tính bằng cm/tuần. Gọi h(t) (tính bằng cm) là độ cao của cây cà chua ở tuần thứ t.

a) Viết công thức xác định hàm số h(t) \((t \ge 0)\).

b) Giai đoạn tăng trưởng của cây cà chua đó kéo dài bao lâu?

c) Chiều cao tối đa của cây cà chua đó là bao nhiêu?

d) Vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua sẽ cao bao nhiêu?

Phương pháp giải - Xem chi tiếtGiải bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều 1

a) Tìm h(t) thông qua v(t).

b) Khảo sát hàm số h(t).

c) Khảo sát hàm số h(t).

d) Khảo sát hàm số v(t).

Lời giải chi tiết

a) \(h(t) = \int {v(t)dt = } \int {\left( { - 0,1{t^3} + {t^2}} \right)} dt = - 0,025{t^4} + \frac{{{t^3}}}{3} + C\)\((t \ge 0)\)

\(h(0) = - 0,{025.0^4} + \frac{{{0^3}}}{3} + C = 5 \Rightarrow C = 5\)

Vậy \(h(t) = - 0,025{t^4} + \frac{{{t^3}}}{3} + 5\)

b) Xét hàm số \(h(t) = - 0,025{t^4} + \frac{{{t^3}}}{3} + 5\)

\(h'(t) = v(t) = - 0,1{t^3} + {t^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0(nghiem\;kep)\\x = 10\end{array} \right.\)

Bảng biến thiên:

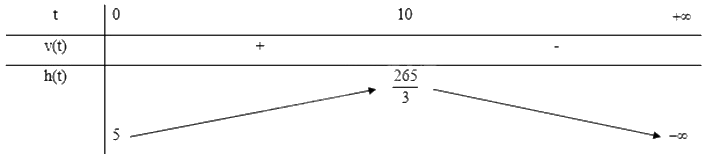
Giải bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều 2

Từ bảng biến thiên ta thấy, giai đoạn tăng trưởng của cây cà chua đó kéo dài 10 tuần.

c) Từ bảng biến thiên ta thấy, chiều cao tối đa của cây cà chua đó là \(\frac{{265}}{3}\) cm.

d) Xét \(v(t) = - 0,1{t^3} + {t^2}\)

\(v'(t) = - 0,3{t^2} + 2t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = \frac{{20}}{3}\end{array} \right.\)

Bảng biến thiên:

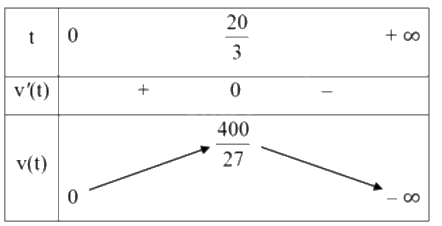
Giải bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều 3

Từ bảng biến thiên ta thấy tốc độ tăng trưởng lớn nhất khi \(t = \frac{{20}}{3}\). Khi đó chiều cao của cây là \(h\left( {\frac{{20}}{3}} \right) = - 0,025{\left( {\frac{{20}}{3}} \right)^4} + \frac{1}{3}{\left( {\frac{{20}}{3}} \right)^3} + 5 = \frac{{4405}}{{81}} \approx 54,38\) (cm).

Giải bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều: Hướng dẫn chi tiết và dễ hiểu

Bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các khái niệm và công thức liên quan.

Nội dung bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều

Bài tập yêu cầu học sinh khảo sát hàm số y = x3 - 3x2 + 2. Cụ thể, các em cần thực hiện các bước sau:

  1. Xác định tập xác định của hàm số.
  2. Tính đạo hàm bậc nhất y' và tìm các điểm cực trị của hàm số.
  3. Lập bảng biến thiên của hàm số.
  4. Vẽ đồ thị hàm số.

Hướng dẫn giải chi tiết bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều

Bước 1: Xác định tập xác định của hàm số

Hàm số y = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là R.

Bước 2: Tính đạo hàm bậc nhất y' và tìm các điểm cực trị của hàm số

Đạo hàm bậc nhất của hàm số là: y' = 3x2 - 6x.

Để tìm các điểm cực trị, ta giải phương trình y' = 0:

3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2.

Vậy hàm số có hai điểm cực trị là x = 0 và x = 2.

Bước 3: Lập bảng biến thiên của hàm số

Ta lập bảng biến thiên như sau:

x-∞02+∞
y'+-+
y↗↘↗

Từ bảng biến thiên, ta thấy hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).

Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2.

Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

Bước 4: Vẽ đồ thị hàm số

Dựa vào bảng biến thiên và các điểm cực trị, ta có thể vẽ được đồ thị hàm số y = x3 - 3x2 + 2.

Lưu ý khi giải bài tập

  • Nắm vững các khái niệm và công thức về đạo hàm.
  • Thực hiện các bước giải một cách cẩn thận và chính xác.
  • Kiểm tra lại kết quả sau khi giải xong.

Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều. Chúc các em học tập tốt!

Ngoài ra, các em có thể tham khảo thêm các bài giải khác tại tusach.vn để hiểu rõ hơn về các kiến thức Toán 12.

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN