Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài tập 7 trang 42 SGK Toán 12 tập 2 - Cánh diều
SGK Toán 12 - Cánh diều
Giải Toán 12 tập 2 - Cánh diều
Chương 4. Nguyên hàm. Tích phân
Bài tập cuối chương 4

Giải bài tập 7 trang 42 SGK Toán 12 tập 2 - Cánh diều

Giải bài tập 7 trang 42 SGK Toán 12 tập 2 - Cánh diều

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 7 trang 42 SGK Toán 12 tập 2 - Cánh diều. Bài tập này thuộc chương trình học Toán 12, tập trung vào kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và các tài liệu học tập hữu ích khác.

Một khinh khí cầu bay với độ cao (so với mực nước biển) tại thời điểm t là h(t), trong đó t tính bằng phút, h(t) tính bằng mét. Tốc độ bay của khinh khí cầu được cho bởi hàm số \(v(t) = - 0,12{t^2} + 1,2t\) với t tính bằng phút, v(t) tính bằng mét/ phút. Tại thời điểm xuất phát (t=0), khinh khí cầu ở độ cao 520m và 5 phút sau khi xuất phát (t = 0), khinh khí cầu ở độ cao 520m và 5 phút sau khi xuất phát, khinh khí cầu đã ở độ cao 530m a) Viết công thức xác định hàm số h(t) \((0 \le t \le 29)\)

Đề bài

Một khinh khí cầu bay với độ cao (so với mực nước biển) tại thời điểm t là h(t), trong đó t tính bằng phút, h(t) tính bằng mét. Tốc độ bay của khinh khí cầu được cho bởi hàm số \(v(t) = - 0,12{t^2} + 1,2t\) với t tính bằng phút, v(t) tính bằng mét/ phút. Tại thời điểm xuất phát (t=0), khinh khí cầu ở độ cao 520m và 5 phút sau khi xuất phát (t = 0), khinh khí cầu ở độ cao 520m và 5 phút sau khi xuất phát, khinh khí cầu đã ở độ cao 530m

a) Viết công thức xác định hàm số h(t) \((0 \le t \le 29)\)

b) Độ cao tối đa của khinh khí cầu khi bay là bao nhiêu?

c) Khi nào khinh khí cầu sẽ trở lại độ cao khi xuất phát?

Phương pháp giải - Xem chi tiếtGiải bài tập 7 trang 42 SGK Toán 12 tập 2 - Cánh diều 1

a) \(h(t) = \int {v(t)} dt\)

b) Khảo sát hàm số h(t)

c) Giải phương trình

Lời giải chi tiết

a) \(h(t) = \int {v(t)} dt = \int {\left( { - 0,12{t^2} + 1,2t} \right)dt} = - 0,04{t^3} + 0,6{t^2} + C\)

Tại t = 0 thì h(0) = 520 => C = 520

Vậy \(h(t) = - 0,04{t^3} + 0,6{t^2} + 520\)

b) Xét \(h(t) = - 0,04{t^3} + 0,6{t^2} + 520\)

\(h'(t) = v(t) = - 0,12{t^2} + 1,2t \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 10\end{array} \right.\)

Bảng biến thiên:

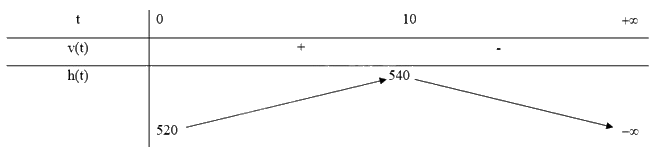
Giải bài tập 7 trang 42 SGK Toán 12 tập 2 - Cánh diều 2

Từ bảng biến thiên, ta thấy độ cao tối đa của khinh khí cầu khi bay là 540m

c) Khinh khí cầu trở lại độ cao xuất phát khi:

\(h(t) = - 0,04{t^3} + 0,6{t^2} + 520 = 520 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 15\end{array} \right.\)

Vậy sau 15 phút thì khinh khí cầu trở lại độ cao xuất phát

Giải bài tập 7 trang 42 SGK Toán 12 tập 2 - Cánh diều: Hướng dẫn chi tiết và dễ hiểu

Bài tập 7 trang 42 SGK Toán 12 tập 2 - Cánh diều là một bài tập quan trọng trong chương trình học Toán 12, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:

Nội dung bài tập 7 trang 42 SGK Toán 12 tập 2 - Cánh diều

Bài tập yêu cầu chúng ta khảo sát hàm số y = x3 - 3x2 + 2. Cụ thể, cần xác định:

  • Tập xác định của hàm số.
  • Các điểm cực trị của hàm số.
  • Khoảng đồng biến, nghịch biến của hàm số.
  • Giới hạn của hàm số khi x tiến tới vô cùng và các điểm tiệm cận (nếu có).
  • Vẽ đồ thị hàm số.

Lời giải chi tiết bài tập 7 trang 42 SGK Toán 12 tập 2 - Cánh diều

  1. Xác định tập xác định: Hàm số y = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.
  2. Tìm đạo hàm: y' = 3x2 - 6x.
  3. Tìm điểm cực trị: Giải phương trình y' = 0, ta được 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2.
  4. Xác định loại cực trị:
    • Với x < 0, y' > 0, hàm số đồng biến.
    • Với 0 < x < 2, y' < 0, hàm số nghịch biến.
    • Với x > 2, y' > 0, hàm số đồng biến.
    Vậy hàm số đạt cực đại tại x = 0, ycđ = 2 và đạt cực tiểu tại x = 2, yct = -2.
  5. Khoảng đồng biến, nghịch biến:
    • Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
    • Hàm số nghịch biến trên khoảng (0; 2).
  6. Giới hạn và tiệm cận:
    • limx→+∞ y = +∞
    • limx→-∞ y = -∞
    Hàm số không có tiệm cận.
  7. Vẽ đồ thị: Dựa vào các kết quả trên, ta có thể vẽ được đồ thị hàm số y = x3 - 3x2 + 2.

Lưu ý khi giải bài tập

Khi giải bài tập về khảo sát hàm số, cần chú ý các bước sau:

  • Xác định đúng tập xác định của hàm số.
  • Tính đạo hàm chính xác.
  • Giải phương trình đạo hàm bằng 0 để tìm điểm cực trị.
  • Xác định đúng loại cực trị và khoảng đồng biến, nghịch biến.
  • Tính giới hạn và tìm tiệm cận (nếu có).
  • Vẽ đồ thị hàm số một cách chính xác.

Các bài tập tương tự

Để củng cố kiến thức, các em có thể tham khảo các bài tập tương tự trong SGK Toán 12 tập 2 - Cánh diều và các tài liệu luyện tập khác.

Chúc các em học tập tốt!

Bài tậpTrang
Bài tập 842
Bài tập 943

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN