Lý thuyết Nguyên hàm của một hàm số sơ cấp Toán 12 Cánh Diều
Nguyên hàm là một khái niệm quan trọng trong giải tích, đóng vai trò then chốt trong việc giải quyết các bài toán tích phân. Bài viết này cung cấp đầy đủ và chi tiết lý thuyết nguyên hàm của một hàm số sơ cấp theo chương trình Toán 12 Cánh Diều, giúp bạn nắm vững kiến thức nền tảng.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, các công thức nguyên hàm cơ bản và phương pháp tìm nguyên hàm của các hàm số sơ cấp thường gặp.
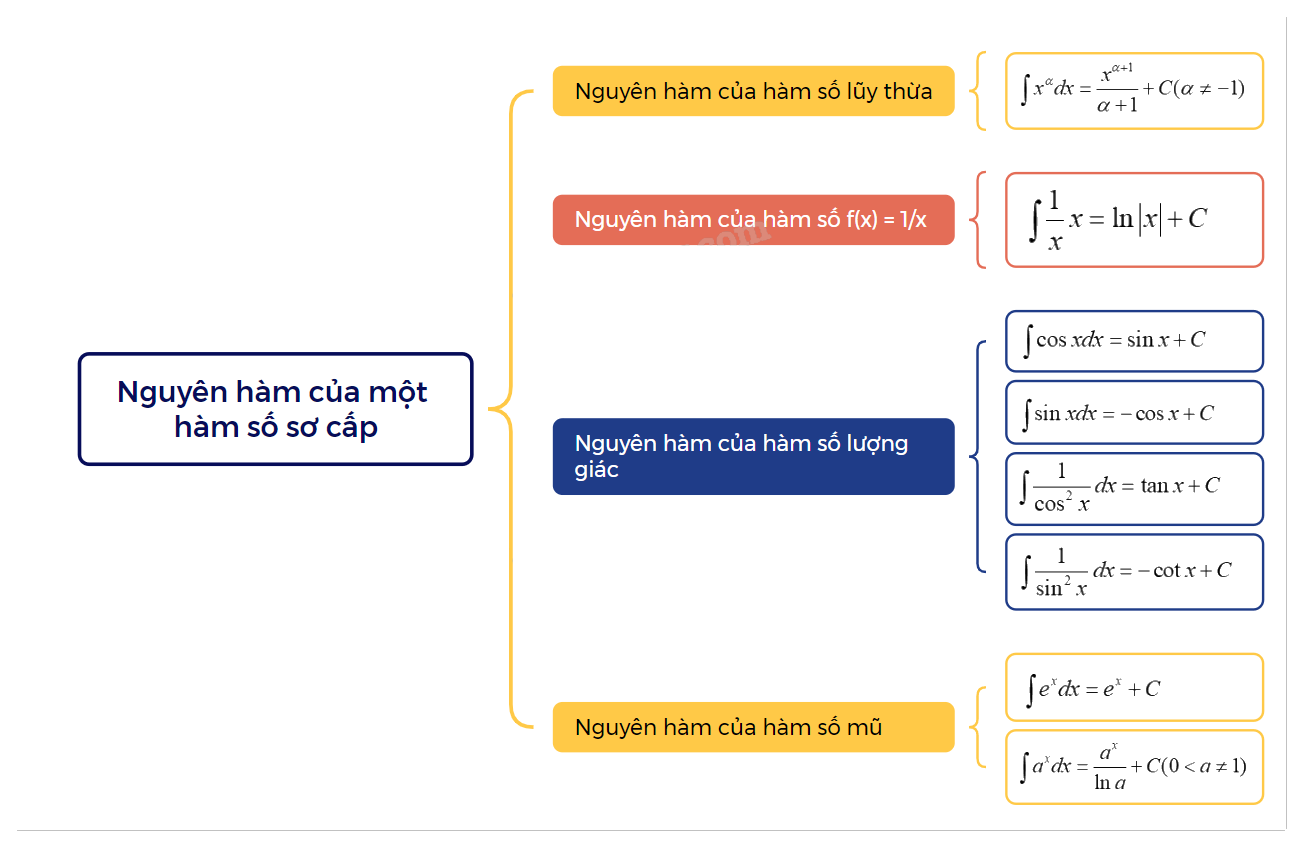
1. Nguyên hàm của hàm số lũy thừa
Hàm số lũy thừa \(y = {x^\alpha }(\alpha \in R)\) có đạo hàm với mọi x > 0 và \(({x^\alpha })' = \alpha {x^{\alpha - 1}}\)
\(\int {{x^\alpha }dx = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C(\alpha \ne - 1)} \)
Lý Thuyết Nguyên Hàm của Một Hàm Số Sơ Cấp Toán 12 Cánh Diều: Tổng Quan Chi Tiết
Nguyên hàm là một khái niệm then chốt trong chương trình Toán 12, đặc biệt là trong phần Giải tích. Hiểu rõ lý thuyết nguyên hàm không chỉ giúp bạn giải quyết các bài toán tích phân một cách hiệu quả mà còn là nền tảng vững chắc cho các kiến thức toán học nâng cao sau này. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết nguyên hàm của một hàm số sơ cấp theo chương trình Toán 12 Cánh Diều.
1. Định Nghĩa Nguyên Hàm
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên khoảng I nếu F'(x) = f(x) với mọi x thuộc I. Ký hiệu: ∫f(x)dx = F(x) + C, trong đó C là hằng số tích phân.
2. Tính Chất của Nguyên Hàm
- Nếu F(x) là một nguyên hàm của f(x) thì F(x) + C cũng là một nguyên hàm của f(x) với mọi hằng số C.
- Hàm số f(x) có vô số nguyên hàm, chúng khác nhau ở hằng số tích phân.
3. Các Công Thức Nguyên Hàm Cơ Bản
Dưới đây là bảng tổng hợp các công thức nguyên hàm cơ bản mà bạn cần nắm vững:
| Hàm số f(x) | Nguyên hàm F(x) |
|---|
| xn (n ≠ -1) | (xn+1)/(n+1) + C |
| 1/x | ln|x| + C |
| ex | ex + C |
| sin(x) | -cos(x) + C |
| cos(x) | sin(x) + C |
| 1/(1+x2) | arctan(x) + C |
4. Các Quy Tắc Tính Nguyên Hàm
- Quy tắc 1: Nguyên hàm của một tổng (hiệu): ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx
- Quy tắc 2: Nguyên hàm của một tích: ∫kf(x)dx = k∫f(x)dx (với k là hằng số)
5. Phương Pháp Tìm Nguyên Hàm
Để tìm nguyên hàm của một hàm số, bạn có thể sử dụng các phương pháp sau:
- Sử dụng các công thức nguyên hàm cơ bản: Xác định hàm số cần tìm nguyên hàm và áp dụng các công thức tương ứng.
- Sử dụng các quy tắc tính nguyên hàm: Phân tích hàm số thành các thành phần đơn giản hơn và áp dụng các quy tắc để tính nguyên hàm.
- Sử dụng phương pháp đổi biến số: Chọn một biến số mới để đơn giản hóa tích phân.
- Sử dụng phương pháp tích phân từng phần: Áp dụng công thức ∫u dv = uv - ∫v du.
6. Ví Dụ Minh Họa
Ví dụ 1: Tìm nguyên hàm của hàm số f(x) = 3x2 + 2x - 1.
Giải:
∫(3x2 + 2x - 1)dx = 3∫x2dx + 2∫xdx - ∫dx = 3(x3/3) + 2(x2/2) - x + C = x3 + x2 - x + C
Ví dụ 2: Tìm nguyên hàm của hàm số f(x) = sin(2x).
Giải:
∫sin(2x)dx. Đặt u = 2x, du = 2dx => dx = du/2
∫sin(u)du/2 = (1/2)∫sin(u)du = (1/2)(-cos(u)) + C = -1/2 cos(2x) + C
7. Luyện Tập và Củng Cố Kiến Thức
Để nắm vững lý thuyết nguyên hàm, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Hãy tìm kiếm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán uy tín như tusach.vn. Việc giải bài tập sẽ giúp bạn hiểu sâu hơn về các khái niệm và công thức, đồng thời rèn luyện kỹ năng giải quyết vấn đề.
Chúc bạn học tốt môn Toán 12!
