Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều

Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.

Mục 2 này tập trung vào các kiến thức quan trọng về... (điền kiến thức chính của mục 2 vào đây). Việc nắm vững kiến thức này là nền tảng cho các bài học tiếp theo.

Điểm cực trị, giá trị cực trị của hàm số

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 9 SGK Toán 12 Cánh diều

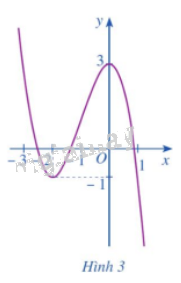
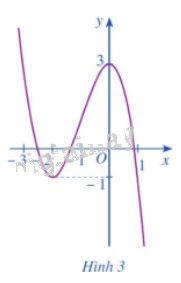
Dựa vào đồ thị hàm số \(y = f\left( x \right) = - {x^3} - 3{x^2} + 3\) ở Hình 3, hãy so sánh:

a) \(f\left( { - 2} \right)\) với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 3; - 1} \right)\) và \(x \ne - 2\).

b) \(f\left( 0 \right)\)với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 1;1} \right)\) và \(x \ne 0\).

Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều 0 1

Phương pháp giải:

Dựa vào đồ thị hàm số

Lời giải chi tiết:

a) Nhận xét: Ta thấy rằng \(f\left( x \right) > f\left( { - 2} \right)\) với mọi \(x \in \left( { - 3; - 1} \right)\) và \(x \ne - 2\).

b) Tương tự: Ta thấy rằng \(f\left( x \right) < f\left( 0 \right)\) với mọi \(x \in \left( { - 1;1} \right)\) và \(x \ne 0\).

LT5

Trả lời câu hỏi Luyện tập 5 trang 11 SGK Toán 12 Cánh diều

Tìm điểm cực trị của mỗi hàm số sau:

a) \(y = {x^4} - 32x + 1\).

b) \(y = \frac{{3x + 5}}{{x - 1}}\).

Phương pháp giải:

B1: Tìm tập xác định của hàm số.

B2: Tính đạo hàm. Tìm các điểm mà tại đó đạo hàm bằng không hoặc không tồn tại.

B3: Lập bảng biến thiên.

B4: Dựa vào bảng biến thiên để kết luận.

Lời giải chi tiết:

a) Tập xác định: \(D = \mathbb{R}\).

Ta có: \(y' = 4{x^3} - 32\).

Xét \(y' = 0 \Leftrightarrow x = 2 \).

Ta có bảng biến thiên sau:

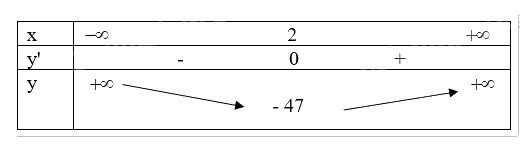
Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều 2 1

Vậy hàm số đạt cực tiểu tại điểm \(x = 2\).

b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).

Ta có: \(y' = \frac{{ - 8}}{{{{\left( {x - 1} \right)}^2}}}\).

Nhận xét \(y' < 0{\rm{ }}\forall x \in D\)

Ta có bảng biến thiên sau:

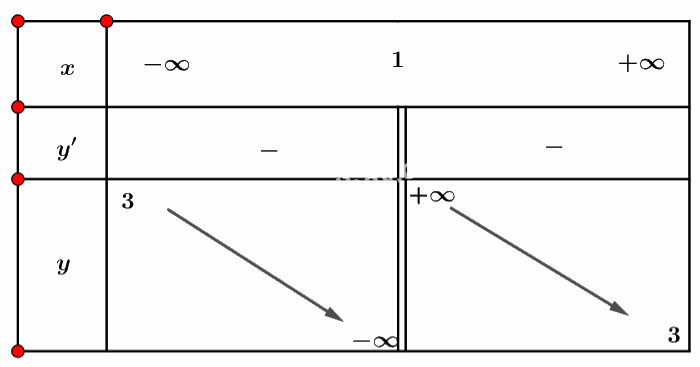
Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều 2 2

Vậy hàm số không có điểm cực trị.

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 10 SGK Toán 12 Cánh diều

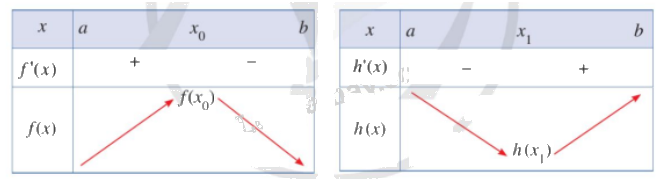
Quan sát bảng biến thiên dưới đây và cho biết:

a) \({x_o}\) có là điểm cực đại của hàm số \(f\left( x \right)\) hay không.

b) \({x_1}\) có là điểm cực tiểu của hàm số \(h\left( x \right)\) hay không.

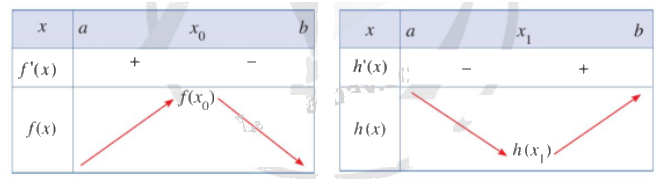
Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều 1 1

Phương pháp giải:

Dựa vào Bảng biến thiên và định nghĩa điểm cực tiểu của hàm số

Lời giải chi tiết:

a) \({x_o}\) có là điểm cực đại của hàm số \(f\left( x \right)\) .

b) \({x_1}\) có là điểm cực tiểu của hàm số \(h\left( x \right)\).

Lựa chọn câu để xem lời giải nhanh hơn

HĐ3
HĐ4
LT5

Trả lời câu hỏi Hoạt động 3 trang 9 SGK Toán 12 Cánh diều

Dựa vào đồ thị hàm số \(y = f\left( x \right) = - {x^3} - 3{x^2} + 3\) ở Hình 3, hãy so sánh:

a) \(f\left( { - 2} \right)\) với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 3; - 1} \right)\) và \(x \ne - 2\).

b) \(f\left( 0 \right)\)với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 1;1} \right)\) và \(x \ne 0\).

Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều 1

Phương pháp giải:

Dựa vào đồ thị hàm số

Lời giải chi tiết:

a) Nhận xét: Ta thấy rằng \(f\left( x \right) > f\left( { - 2} \right)\) với mọi \(x \in \left( { - 3; - 1} \right)\) và \(x \ne - 2\).

b) Tương tự: Ta thấy rằng \(f\left( x \right) < f\left( 0 \right)\) với mọi \(x \in \left( { - 1;1} \right)\) và \(x \ne 0\).

Trả lời câu hỏi Hoạt động 4 trang 10 SGK Toán 12 Cánh diều

Quan sát bảng biến thiên dưới đây và cho biết:

a) \({x_o}\) có là điểm cực đại của hàm số \(f\left( x \right)\) hay không.

b) \({x_1}\) có là điểm cực tiểu của hàm số \(h\left( x \right)\) hay không.

Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều 2

Phương pháp giải:

Dựa vào Bảng biến thiên và định nghĩa điểm cực tiểu của hàm số

Lời giải chi tiết:

a) \({x_o}\) có là điểm cực đại của hàm số \(f\left( x \right)\) .

b) \({x_1}\) có là điểm cực tiểu của hàm số \(h\left( x \right)\).

Trả lời câu hỏi Luyện tập 5 trang 11 SGK Toán 12 Cánh diều

Tìm điểm cực trị của mỗi hàm số sau:

a) \(y = {x^4} - 32x + 1\).

b) \(y = \frac{{3x + 5}}{{x - 1}}\).

Phương pháp giải:

B1: Tìm tập xác định của hàm số.

B2: Tính đạo hàm. Tìm các điểm mà tại đó đạo hàm bằng không hoặc không tồn tại.

B3: Lập bảng biến thiên.

B4: Dựa vào bảng biến thiên để kết luận.

Lời giải chi tiết:

a) Tập xác định: \(D = \mathbb{R}\).

Ta có: \(y' = 4{x^3} - 32\).

Xét \(y' = 0 \Leftrightarrow x = 2 \).

Ta có bảng biến thiên sau:

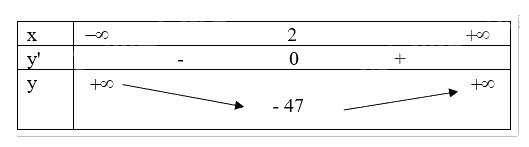
Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều 3

Vậy hàm số đạt cực tiểu tại điểm \(x = 2\).

b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).

Ta có: \(y' = \frac{{ - 8}}{{{{\left( {x - 1} \right)}^2}}}\).

Nhận xét \(y' < 0{\rm{ }}\forall x \in D\)

Ta có bảng biến thiên sau:

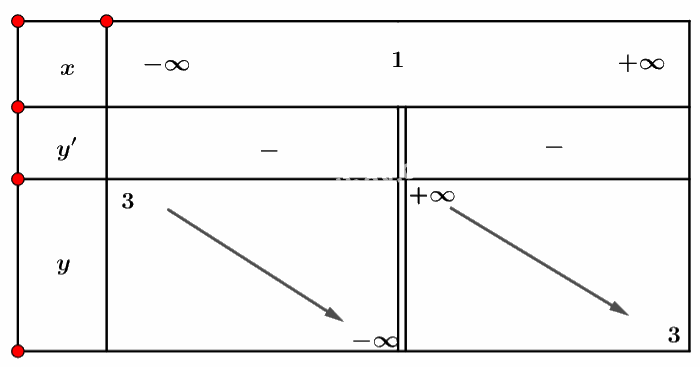
Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều 4

Vậy hàm số không có điểm cực trị.

Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều: Hướng dẫn chi tiết và dễ hiểu

Mục 2 trong SGK Toán 12 tập 1 - Cánh diều là một phần quan trọng, đặt nền móng cho việc hiểu và vận dụng các kiến thức về... (điền kiến thức chính của mục 2 vào đây). Nhiều học sinh gặp khó khăn khi giải các bài tập trong mục này, do đó, tusach.vn xin giới thiệu bài viết hướng dẫn chi tiết, dễ hiểu, giúp các em tự tin chinh phục các bài tập.

Nội dung chính của Mục 2 SGK Toán 12 tập 1 - Cánh diều

Mục 2 tập trung vào việc... (liệt kê các nội dung chính của mục 2, ví dụ: ôn tập về hàm số, giới thiệu về đạo hàm, các quy tắc tính đạo hàm...). Để hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng bài tập trong trang 9, 10 và 11.

Giải chi tiết bài tập trang 9 SGK Toán 12 tập 1 - Cánh diều

Bài 1: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích rõ ràng từng bước).
Bài 2: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích rõ ràng từng bước).
...(Tiếp tục giải các bài tập còn lại trên trang 9)

Giải chi tiết bài tập trang 10 SGK Toán 12 tập 1 - Cánh diều

Bài 3: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích rõ ràng từng bước).
Bài 4: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích rõ ràng từng bước).
...(Tiếp tục giải các bài tập còn lại trên trang 10)

Giải chi tiết bài tập trang 11 SGK Toán 12 tập 1 - Cánh diều

Bài 5: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích rõ ràng từng bước).
Bài 6: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, kèm theo giải thích rõ ràng từng bước).
...(Tiếp tục giải các bài tập còn lại trên trang 11)

Lưu ý khi giải bài tập Mục 2 SGK Toán 12 tập 1 - Cánh diều

Nắm vững các định nghĩa, định lý và công thức liên quan.
Đọc kỹ đề bài, xác định đúng yêu cầu của bài toán.
Sử dụng các phương pháp giải toán phù hợp.
Kiểm tra lại kết quả sau khi giải xong.

Tusach.vn – Đồng hành cùng bạn học Toán 12

Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong SGK Toán 12 tập 1 - Cánh diều. Hãy truy cập tusach.vn để học Toán 12 hiệu quả và đạt kết quả cao!

Ngoài ra, các bạn có thể tham khảo thêm các tài liệu học tập khác tại tusach.vn, bao gồm:

Bài giảng Toán 12
Đề thi thử Toán 12
Các bài tập trắc nghiệm Toán 12

Chúc các em học tập tốt!

Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều

Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều

HĐ3

LT5

HĐ4

Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều: Hướng dẫn chi tiết và dễ hiểu

Nội dung chính của Mục 2 SGK Toán 12 tập 1 - Cánh diều

Giải chi tiết bài tập trang 9 SGK Toán 12 tập 1 - Cánh diều

Giải chi tiết bài tập trang 10 SGK Toán 12 tập 1 - Cánh diều

Giải chi tiết bài tập trang 11 SGK Toán 12 tập 1 - Cánh diều

Lưu ý khi giải bài tập Mục 2 SGK Toán 12 tập 1 - Cánh diều

Tusach.vn – Đồng hành cùng bạn học Toán 12

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN