Logo

Giải bài tập 12 trang 83 SGK Toán 12 tập 1 - Cánh diều

Tổng quan nội dung

Giải Bài Tập 12 Trang 83 Toán 12 Tập 1 Cánh Diều

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 12 trang 83 SGK Toán 12 tập 1 Cánh Diều. Bài viết này sẽ cung cấp đáp án chính xác và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho các em học sinh.

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AA’ và CC’. Tính góc giữa hai vecto \(\overrightarrow {MN} \) và \(\overrightarrow {AD'} \)

Đề bài

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AA’ và CC’. Tính góc giữa hai vecto \(\overrightarrow {MN} \) và \(\overrightarrow {AD'} \)

Phương pháp giải - Xem chi tiếtGiải bài tập 12 trang 83 SGK Toán 12 tập 1 - Cánh diều 1

\(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)

Lời giải chi tiết

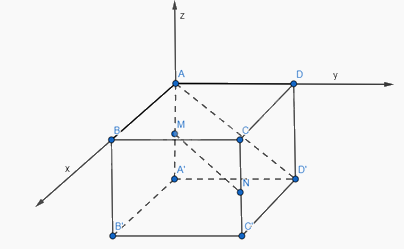
Giải bài tập 12 trang 83 SGK Toán 12 tập 1 - Cánh diều 2

Đặt \(A \equiv O(0;0;0)\)

Ta có: \(D'(0;a;a)\); \(M(0;0; - \frac{a}{2})\); \(N(a;a; - \frac{a}{2})\)

\(\overrightarrow {MN} = (a;a;0)\);\(\overrightarrow {AD'} = (0;a;a)\)

\(\cos (\overrightarrow {MN} ,\overrightarrow {AD'} ) = \frac{{\overrightarrow {MN} .\overrightarrow {AD'} }}{{\left| {\overrightarrow {MN} } \right|.\left| {\overrightarrow {AD'} } \right|}} = \frac{{a.a}}{{\sqrt {{a^2} + {a^2}} .\sqrt {{a^2} + {a^2}} }} = \frac{{{a^2}}}{{2{a^2}}} = \frac{1}{2} \Rightarrow (\overrightarrow {MN} ,\overrightarrow {AD'} ) = 60^\circ \)

Giải Bài Tập 12 Trang 83 SGK Toán 12 Tập 1 Cánh Diều: Chi Tiết và Dễ Hiểu

Bài tập 12 trang 83 SGK Toán 12 tập 1 Cánh Diều thuộc chương trình học về đạo hàm. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học nâng cao hơn. Việc nắm vững phương pháp giải các bài tập về đạo hàm sẽ giúp học sinh giải quyết các bài toán phức tạp một cách hiệu quả.

Nội dung bài tập 12 trang 83 SGK Toán 12 Tập 1 Cánh Diều

Bài tập 12 yêu cầu học sinh tính đạo hàm của hàm số tại một điểm cho trước. Cụ thể, bài tập thường có dạng:

  • Cho hàm số f(x) = ... Tính f'(x0)

Để giải bài tập này, học sinh cần nắm vững các quy tắc tính đạo hàm cơ bản như:

  • Đạo hàm của hàm số lũy thừa
  • Đạo hàm của hàm số đa thức
  • Đạo hàm của hàm số lượng giác
  • Đạo hàm của hàm số mũ và logarit
  • Quy tắc đạo hàm của tổng, hiệu, tích, thương và hàm hợp

Phương pháp giải bài tập 12 trang 83 SGK Toán 12 Tập 1 Cánh Diều

  1. Xác định hàm số f(x) và điểm x0.
  2. Áp dụng các quy tắc tính đạo hàm để tìm đạo hàm f'(x).
  3. Thay x = x0 vào f'(x) để tính f'(x0).

Ví dụ minh họa giải bài tập 12 trang 83 SGK Toán 12 Tập 1 Cánh Diều

Ví dụ: Cho hàm số f(x) = x2 + 2x - 1. Tính f'(2).

Giải:

  1. f(x) = x2 + 2x - 1, x0 = 2
  2. f'(x) = 2x + 2 (áp dụng quy tắc đạo hàm của hàm đa thức)
  3. f'(2) = 2(2) + 2 = 6

Vậy f'(2) = 6.

Lưu ý khi giải bài tập về đạo hàm

  • Nắm vững các quy tắc tính đạo hàm cơ bản.
  • Chú ý đến thứ tự thực hiện các phép toán.
  • Kiểm tra lại kết quả sau khi tính toán.
  • Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.

Tài liệu tham khảo thêm

Ngoài SGK Toán 12 tập 1 Cánh Diều, các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:

  • Sách bài tập Toán 12
  • Các trang web học Toán trực tuyến
  • Các video bài giảng Toán 12

Kết luận

Hy vọng với lời giải chi tiết và phương pháp giải bài tập 12 trang 83 SGK Toán 12 tập 1 Cánh Diều trên đây, các em học sinh sẽ hiểu rõ hơn về kiến thức đạo hàm và tự tin hơn trong quá trình học tập. Chúc các em học tốt!

Hàm sốĐạo hàm
f(x) = xnf'(x) = nxn-1
f(x) = sin(x)f'(x) = cos(x)