Đề bài
Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt E(0;0;6) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là \({A_1}(0;1;0)\), \({A_2}(\frac{{\sqrt 3 }}{2}; - \frac{1}{2};0)\), \({A_3}( - \frac{{\sqrt 3 }}{2}; - \frac{1}{2};0)\) (Hình 40). Biết rằng trọng lượng của chiếc máy là 300N. Tìm tọa độ của các lực tác dụng lên giá đỡ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \)
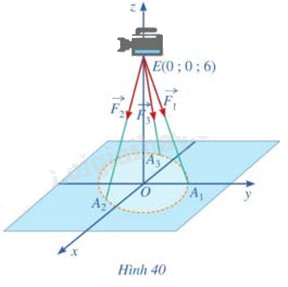
Phương pháp giải - Xem chi tiết
Vì đèn cân bằng nên trọng lực của đèn sẽ phân bố đều trên các chân của giá đỡ. Từ tọa độ các điểm đã cho, ta tìm được cái mối liên hệ với vecto lực và tìm được tọa độ của các vecto lực
Lời giải chi tiết
Ta có:
\(\left| {\overrightarrow {{A_1}O} } \right| = \sqrt {{{(0 - 0)}^2} + {{(1 - 0)}^2} + {{(0 - 0)}^2}} = 1\);
\(\left| {\overrightarrow {{A_2}O} } \right| = \sqrt {{{\left( {\frac{{\sqrt 3 }}{2} - 0} \right)}^2} + {{\left( { - \frac{1}{2} - 0} \right)}^2} + {{(0 - 0)}^2}} = 1\);
\(\left| {\overrightarrow {{A_3}O} } \right| = \sqrt {{{\left( { - \frac{{\sqrt 3 }}{2} - 0} \right)}^2} + {{\left( { - \frac{1}{2} - 0} \right)}^2} + {{(0 - 0)}^2}} = 1\).
Do đó \({A_1}O = {A_2}O = {A_3}O = 1\), suy ra O là trọng tâm tam giác \({A_1}{A_2}{A_3}\).
Khi đó \(\overrightarrow {E{A_1}} + \overrightarrow {E{A_2}} + \overrightarrow {E{A_3}} = 3\overrightarrow {EO} \) (tính chất trọng tâm).
Mặt khác, dễ dàng chứng minh độ dài các giá đỡ \(E{A_1} = E{A_2} = E{A_3}\) (do các tam giác vuông \(EO{A_1}\), \(EO{A_2}\), \(EO{A_3}\) bằng nhau). Các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) cùng phương với các giá đỡ và có độ lớn bằng nhau nên ta có tỉ lệ:
\(\frac{{\left| {\overrightarrow {{F_1}} } \right|}}{{E{A_1}}} = \frac{{\left| {\overrightarrow {{F_2}} } \right|}}{{E{A_2}}} = \frac{{\left| {\overrightarrow {{F_3}} } \right|}}{{E{A_3}}} = k\) và \(\overrightarrow {{F_1}} = k\overrightarrow {E{A_1}} \), \(\overrightarrow {{F_2}} = k\overrightarrow {E{A_2}} \), \(\overrightarrow {{F_3}} = k\overrightarrow {E{A_3}} \).
Từ \(\overrightarrow {E{A_1}} + \overrightarrow {E{A_2}} + \overrightarrow {E{A_3}} = 3\overrightarrow {EO} \) đã chứng minh, ta được:
\(k\overrightarrow {E{A_1}} + k\overrightarrow {E{A_2}} + k\overrightarrow {E{A_3}} = 3k\overrightarrow {EO} \)
\( \Leftrightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = 3k\overrightarrow {EO} \).
Mà \(\overrightarrow {EO} = (0 - 0;0 - 0;0 - 6) = (0;0 - 6)\).
Suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = (0;0; - 18k)\).
Giả sử \(\overrightarrow P \) là trọng lực tác động lên cả 3 giá đỡ. \(\overrightarrow P \) là lực vuông góc với mặt phẳng (Oxy), hướng xuống dưới (ngược chiều với trục Oz) nên tọa độ của \(\overrightarrow P = (0;0; - 300)\).
Suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \Leftrightarrow - 18k = - 300 \Leftrightarrow k = \frac{{50}}{3}\).
Vậy \(\overrightarrow {{F_1}} = (0;\frac{{50}}{3}; - 100)\); \(\overrightarrow {{F_2}} = (\frac{{25\sqrt 3 }}{3}; - \frac{{25}}{3}; - 100)\); \(\overrightarrow {{F_3}} = ( - \frac{{25\sqrt 3 }}{3}; - \frac{{25}}{3}; - 100)\).
