Giải bài tập 1 trang 13 SGK Toán 12 tập 1 - Cánh diều
Tổng quan nội dung
Giải Bài Tập 1 Trang 13 Toán 12 Tập 1 Cánh Diều
Chào mừng bạn đến với lời giải chi tiết bài tập 1 trang 13 SGK Toán 12 tập 1 Cánh Diều trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp bạn hiểu sâu sắc kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, hỗ trợ tối đa cho quá trình học tập của bạn.
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau: Hàm số đồng biến trên khoảng nào dưới đây? A. \(\left( {1; + \infty } \right)\). B. \(\left( { - 1;0} \right)\). C. \(\left( { - 1;1} \right)\). D. \(\left( {0;1} \right)\).
Đề bài
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau:
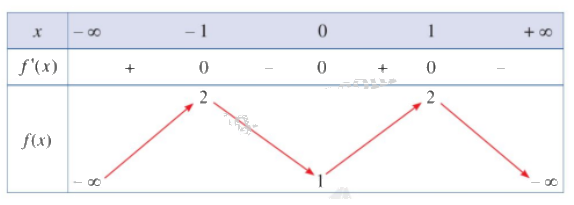 Hàm số đồng biến trên khoảng nào dưới đây?A. \(\left( {1; + \infty } \right)\). B. \(\left( { - 1;0} \right)\). C. \(\left( { - 1;1} \right)\). D. \(\left( {0;1} \right)\).
Hàm số đồng biến trên khoảng nào dưới đây?A. \(\left( {1; + \infty } \right)\). B. \(\left( { - 1;0} \right)\). C. \(\left( { - 1;1} \right)\). D. \(\left( {0;1} \right)\).
Phương pháp giải - Xem chi tiết
Dựa vào bảng biến thiên để nhận xét.
Lời giải chi tiết
Dựa vào bảng biến thiên ta thấy đồ thị hàm số đi lên trong khoảng \(\left( {0;1} \right)\) nên hàm số đồng biến trên khoảng \(\left( {0;1} \right) \Rightarrow D\).
Giải Bài Tập 1 Trang 13 Toán 12 Tập 1 Cánh Diều: Tổng Quan và Phương Pháp Giải Chi Tiết
Bài tập 1 trang 13 SGK Toán 12 tập 1 Cánh Diều thuộc chương trình học về Hàm số bậc hai. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học toán ở các lớp cao hơn. Việc nắm vững kiến thức về hàm số bậc hai, đặc biệt là cách xác định các yếu tố của hàm số (hệ số a, b, c), đỉnh của parabol, trục đối xứng, và khoảng đồng biến, nghịch biến là vô cùng cần thiết.
Nội Dung Bài Tập 1 Trang 13 SGK Toán 12 Tập 1 Cánh Diều
Bài tập 1 yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai, xác định đỉnh của parabol, trục đối xứng và vẽ đồ thị hàm số. Để giải bài tập này, bạn cần nắm vững các công thức và định nghĩa sau:
- Hàm số bậc hai: y = ax2 + bx + c (a ≠ 0)
- Hệ số a, b, c: Các số thực a, b, c được gọi là hệ số của hàm số bậc hai.
- Đỉnh của parabol: I(x0; y0) với x0 = -b/2a và y0 = f(x0)
- Trục đối xứng: Đường thẳng x = x0
Hướng Dẫn Giải Chi Tiết Bài Tập 1a, 1b, 1c, 1d
Chúng ta sẽ cùng nhau giải chi tiết từng phần của bài tập 1:
Bài 1a: y = x2 - 4x + 3
- Xác định hệ số: a = 1, b = -4, c = 3
- Tính tọa độ đỉnh: x0 = -(-4)/(2*1) = 2; y0 = 22 - 4*2 + 3 = -1. Vậy đỉnh I(2; -1)
- Xác định trục đối xứng: x = 2
- Vẽ đồ thị: Xác định một vài điểm thuộc đồ thị (ví dụ: điểm cắt trục Oy là (0; 3), điểm cắt trục Ox là (1; 0) và (3; 0)) và vẽ parabol.
Bài 1b: y = -2x2 + 5x - 3
(Tương tự như bài 1a, bạn tự giải)
Bài 1c: y = 3x2 + 2x
(Tương tự như bài 1a, bạn tự giải)
Bài 1d: y = -x2 + 1
(Tương tự như bài 1a, bạn tự giải)
Lưu Ý Quan Trọng Khi Giải Bài Tập Hàm Số Bậc Hai
- Luôn kiểm tra điều kiện a ≠ 0 để đảm bảo hàm số là hàm số bậc hai.
- Sử dụng đúng công thức để tính tọa độ đỉnh và trục đối xứng.
- Vẽ đồ thị hàm số một cách chính xác, chú ý đến các điểm đặc biệt như đỉnh, điểm cắt trục.
Ứng Dụng Của Hàm Số Bậc Hai Trong Thực Tế
Hàm số bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
- Vật lý: Mô tả quỹ đạo của vật ném, chuyển động của các vật thể chịu tác dụng của trọng lực.
- Kinh tế: Tính toán lợi nhuận, chi phí, doanh thu.
- Kỹ thuật: Thiết kế các công trình xây dựng, cầu cống.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, bạn đã nắm vững cách giải bài tập 1 trang 13 SGK Toán 12 tập 1 Cánh Diều. Hãy luyện tập thêm nhiều bài tập khác để củng cố kiến thức và nâng cao kỹ năng giải toán của mình. Chúc bạn học tốt!
Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại để lại bình luận bên dưới. tusach.vn luôn sẵn sàng hỗ trợ bạn.