Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều
SGK Toán 12 - Cánh diều
Giải Toán 12 tập 1 - Cánh diều
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Bài tập cuối chương 1

Giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều

Giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều

Bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học Toán 12, tập trung vào việc rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ bản chất và phương pháp giải, từ đó tự tin hơn trong các bài kiểm tra và thi cử.

Có hai xã A,B cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA’ =500m, BB’=600m và người ta đo được A’B’= 2.200m(hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn A’B’ sao cho tổng khoảng cách từ hai xa đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.

Đề bài

Có hai xã A,B cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA’ =500m, BB’=600m và người ta đo được A’B’= 2.200m(hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn A’B’ sao cho tổng khoảng cách từ hai xa đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.

Giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều 1

Phương pháp giải - Xem chi tiếtGiải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều 2

- Phân tích đề bài

- Tìm mối liên hệ trong bài

Lời giải chi tiết

Đặt A'M = x (m).

Suy ra B'M = A'B' – A'M = 2200 – x (m).

Rõ ràng, x phải thỏa mãn điều kiện 0 < x < 2200.

Áp dụng định lí Pythagore ta tính được:

\(AM = \sqrt {A'{A^2} + A'{M^2}} {\rm{\;}} = \sqrt {{{500}^2} + {x^2}} \) (m)

\(BM = \sqrt {B'{B^2} + B'{M^2}} {\rm{\;}} = \sqrt {{{600}^2} + {{(2200 - x)}^2}} \) (m)

Tổng khoảng cách từ hai vị trí A, B đến vị trí M là

\(D = AM + BM = \sqrt {{{500}^2} + {x^2}} {\rm{\;}} + \sqrt {{{600}^2} + {{(2200 - x)}^2}} \) (m)

Xét hàm số \(D(x) = \sqrt {{{500}^2} + {x^2}} {\rm{\;}} + \sqrt {{{600}^2} + (2200 - {x^2})} \) với \(x \in (0;2200)\).

\(D'(x) = \frac{{2x}}{{2\sqrt {{{500}^2} + {x^2}} }} + \frac{{2x - 4400}}{{\sqrt {{{600}^2} + {{(2200 - x)}^2}} }} = \frac{x}{{\sqrt {{{500}^2} + {x^2}} }} + \frac{{x - 2200}}{{\sqrt {{{600}^2} + {{(2200 - x)}^2}} }}\).

Trên khoảng (0;2200), ta thấy D'(x) = 0 khi x = 1000.

Bảng biến thiên của hàm số D(x) như sau:

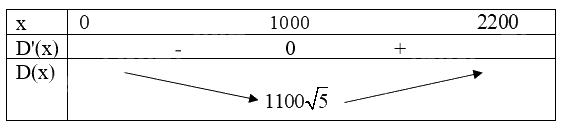
Giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều 3

Căn cứ vào bảng biến thiên, ta thấy hàm số D(x) đạt giá trị nhỏ nhất bằng \(1100\sqrt 5 \) tại x = 1 000.

Vậy giá trị nhỏ nhất của tổng khoảng cách cần tìm là \(1100\sqrt 5 \) m.

Giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều: Hướng dẫn chi tiết và dễ hiểu

Bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế liên quan đến việc tìm cực trị của hàm số.

Nội dung bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều

Bài tập 13 thường có dạng như sau: Cho hàm số y = f(x). Tìm các điểm cực trị của hàm số. Hoặc, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.

Phương pháp giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều

  1. Bước 1: Tính đạo hàm f'(x). Đây là bước quan trọng nhất để xác định các điểm cực trị của hàm số.
  2. Bước 2: Tìm các điểm làm đạo hàm bằng 0 hoặc không xác định. Các điểm này là các điểm nghi ngờ là cực trị.
  3. Bước 3: Lập bảng biến thiên của hàm số. Bảng biến thiên giúp ta xác định khoảng đồng biến, nghịch biến của hàm số và từ đó xác định các điểm cực trị.
  4. Bước 4: Kết luận về các điểm cực trị. Dựa vào bảng biến thiên, ta kết luận về các điểm cực đại, cực tiểu của hàm số.

Ví dụ minh họa giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều

Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.

Giải:

  • Bước 1: Tính đạo hàm: y' = 3x2 - 6x
  • Bước 2: Tìm các điểm làm đạo hàm bằng 0: 3x2 - 6x = 0 => x = 0 hoặc x = 2
  • Bước 3: Lập bảng biến thiên:
x-∞02+∞
y'+-+
yNBĐCTCNB

Chú thích: NB - Nghịch biến, ĐC - Đồng biến, TC - Tăng, Giảm

  • Bước 4: Kết luận: Hàm số đạt cực đại tại x = 0, yCĐ = 2 và đạt cực tiểu tại x = 2, yCT = -2.

    • Lưu ý khi giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều

    • Luôn kiểm tra điều kiện xác định của hàm số.
    • Chú ý đến các điểm không xác định của đạo hàm.
    • Vẽ bảng biến thiên một cách chính xác để xác định các điểm cực trị.
    • Kiểm tra lại kết quả bằng cách sử dụng các phương pháp khác.

    Tại sao nên chọn tusach.vn để giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều?

    tusach.vn cung cấp:

    • Lời giải chi tiết, dễ hiểu, được trình bày rõ ràng.
    • Đội ngũ giáo viên giàu kinh nghiệm, chuyên môn cao.
    • Cập nhật liên tục các bài giải mới nhất.
    • Giao diện thân thiện, dễ sử dụng.

    Hãy truy cập tusach.vn ngay hôm nay để được hỗ trợ giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều và các bài tập Toán 12 khác!

    Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

    CHỦ ĐỀ SÁCH XEM NHIỀU

    Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

    VỀ TUSACH.VN