Giải Bài Tập 7 Trang 81 Toán 12 Tập 1 Cánh Diều

Giải bài tập 7 trang 81 SGK Toán 12 tập 1 - Cánh diều

Giải Bài Tập 7 Trang 81 Toán 12 Tập 1 Cánh Diều

Bài tập 7 trang 81 SGK Toán 12 tập 1 Cánh Diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Cho hình hộp ABCD.A’B’C’D’, biết A(1;0;1), B(2;1;2), D(1;-1;1), C’(4;5;-5). Hãy chỉ ra tọa độ của một vecto khác (overrightarrow 0 ) vuông góc với cả hai vecto trong mỗi trường hợp sau: a) (overrightarrow {AC} ) và (overrightarrow {B'D'} ) b) (overrightarrow {AC'} ) và (overrightarrow {BD} )

Đề bài

Cho hình hộp ABCD.A’B’C’D’, biết A(1;0;1), B(2;1;2), D(1;-1;1), C’(4;5;-5). Hãy chỉ ra tọa độ của một vecto khác \(\overrightarrow 0 \) vuông góc với cả hai vecto trong mỗi trường hợp sau:

a) \(\overrightarrow {AC} \) và \(\overrightarrow {B'D'} \)

b) \(\overrightarrow {AC'} \) và \(\overrightarrow {BD} \)

Phương pháp giải - Xem chi tiết Giải bài tập 7 trang 81 SGK Toán 12 tập 1 - Cánh diều 1

Cho hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) không cùng phương. Khi đó, vecto \(\overrightarrow w = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \)

Lời giải chi tiết

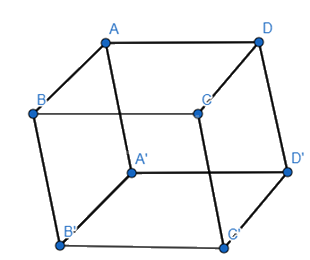
Giải bài tập 7 trang 81 SGK Toán 12 tập 1 - Cánh diều 2

a) Ta có: \(\overrightarrow {AB} = (1;1;1),\overrightarrow {AD} = (0; - 1;0)\)

\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {AC} = (1;0;1\))

\(\overrightarrow {B'D'} = \overrightarrow {BD} = ( - 1; - 2; -1 )\)

\([\overrightarrow {AC} ,\overrightarrow {B'D'} ] = \left( {\left| \begin{array}{l}\;\;\;0\;\;\;\;1\\ - 2\;\;\;\;\;1\end{array} \right|;\left| \begin{array}{l}1\;\;\;\;\;\;1\\\;-1\;\;\;\;\; - 1\end{array} \right|;\left| \begin{array}{l}1\;\;\;\;\;\;\;0\\ - 1\;\;\;\; - 2\end{array} \right|} \right) = (2; 0;- 2)\)

Chọn \(\overrightarrow u = (2; 0; - 2)\) vuông góc với cả hai vecto \(\overrightarrow {AC} \) và \(\overrightarrow {B'D'} \).

b) \(\overrightarrow {AC'} = (3;5; - 6)\), \(\overrightarrow {BD} = ( - 1; - 2; - 1)\)

\([\overrightarrow {AC'} ,\overrightarrow {BD} ] = \left( {\left| \begin{array}{l}\;\;\;5\;\;\;\; - 6\\ - 2\;\;\;\;\; - 1\end{array} \right|;\left| \begin{array}{l} - 6\;\;\;\;\;\;3\\\; - 1\;\;\;\;\; - 1\end{array} \right|;\left| \begin{array}{l}3\;\;\;\;\;\;\;5\\ - 1\;\;\;\; - 2\end{array} \right|} \right) = ( - 17;9; - 1)\)

Chọn \(\overrightarrow v = ( - 17;9; - 1)\) vuông góc với cả hai vecto \(\overrightarrow {AC'} \) và \(\overrightarrow {BD} \).

Giải Bài Tập 7 Trang 81 SGK Toán 12 Tập 1 Cánh Diều: Hướng Dẫn Chi Tiết và Phương Pháp Giải

Bài tập 7 trang 81 SGK Toán 12 tập 1 Cánh Diều thuộc chương trình học về đạo hàm của hàm số. Đây là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:

Nội dung Bài Tập 7 Trang 81 Toán 12 Tập 1 Cánh Diều

Bài tập yêu cầu tính đạo hàm của hàm số f(x) = x³ - 3x² + 2x - 1 tại một điểm x cụ thể. Để giải bài tập này, học sinh cần nắm vững các quy tắc tính đạo hàm cơ bản, bao gồm:

Đạo hàm của xⁿ là nx^n-1
Đạo hàm của một hằng số là 0
Đạo hàm của tổng (hoặc hiệu) các hàm số là tổng (hoặc hiệu) các đạo hàm

Phương Pháp Giải Bài Tập 7 Trang 81 Toán 12 Tập 1 Cánh Diều

Để giải bài tập này, chúng ta thực hiện các bước sau:

Tính đạo hàm f'(x) của hàm số f(x) bằng cách áp dụng các quy tắc đạo hàm đã nêu ở trên.
Thay giá trị x cụ thể vào f'(x) để tính đạo hàm tại điểm đó.

Lời Giải Chi Tiết Bài Tập 7 Trang 81 Toán 12 Tập 1 Cánh Diều

Bước 1: Tính đạo hàm f'(x)

f(x) = x³ - 3x² + 2x - 1

f'(x) = 3x² - 6x + 2

Bước 2: Thay x vào f'(x)

Giả sử x = 2, ta có:

f'(2) = 3(2)² - 6(2) + 2 = 12 - 12 + 2 = 2

Vậy, đạo hàm của hàm số f(x) tại x = 2 là 2.

Mở Rộng và Bài Tập Tương Tự

Để hiểu rõ hơn về đạo hàm, bạn có thể thực hành với các bài tập tương tự. Ví dụ:

Tính đạo hàm của hàm số g(x) = 2x⁴ + x² - 5x + 3
Tìm đạo hàm của hàm số h(x) = (x² + 1)(x - 2)

Lưu Ý Khi Giải Bài Tập Về Đạo Hàm

Khi giải các bài tập về đạo hàm, bạn cần lưu ý những điều sau:

Nắm vững các quy tắc đạo hàm cơ bản.
Áp dụng đúng quy tắc đạo hàm cho từng loại hàm số.
Kiểm tra lại kết quả sau khi tính toán.

Tại Sao Nên Chọn tusach.vn Để Học Toán 12?

tusach.vn là một nguồn tài liệu học tập Toán 12 uy tín và chất lượng. Chúng tôi cung cấp:

Lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK Toán 12.
Các bài giảng video hấp dẫn và sinh động.
Các bài kiểm tra trắc nghiệm giúp bạn tự đánh giá kiến thức.
Đội ngũ giáo viên giàu kinh nghiệm sẵn sàng hỗ trợ bạn.

Hãy truy cập tusach.vn ngay hôm nay để học Toán 12 hiệu quả và đạt kết quả cao!

Quy tắc	Ví dụ
Đạo hàm của xⁿ	(x²)' = 2x
Đạo hàm của hằng số	(5)' = 0

Giải bài tập 7 trang 81 SGK Toán 12 tập 1 - Cánh diều