Giải Bài Tập 2 Trang 92 Toán 12 Tập 1 Cánh Diều

Giải bài tập 2 trang 92 SGK Toán 12 tập 1 - Cánh diều

Giải Bài Tập 2 Trang 92 Toán 12 Tập 1 Cánh Diều

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2 trang 92 SGK Toán 12 tập 1 Cánh Diều. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu sâu hơn về kiến thức đã học.

tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.

Bảng 19, Bảng 20 lần lượt biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của hai công ty A, B (đơn vị: triệu đồng) a) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm lần lượt biểu diễn mức lương của hai công ty A,B b) Công ty nào có mức lương đồng đều hơn?

Đề bài

Bảng 19, Bảng 20 lần lượt biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của hai công ty A, B (đơn vị: triệu đồng)

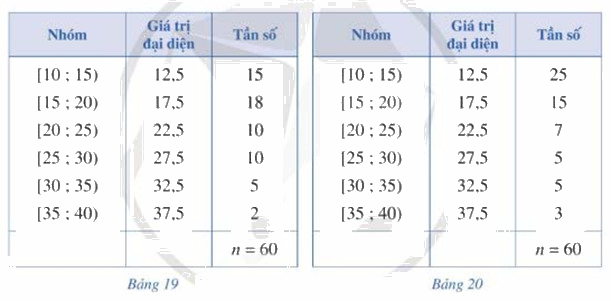
Giải bài tập 2 trang 92 SGK Toán 12 tập 1 - Cánh diều 1

a) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm lần lượt biểu diễn mức lương của hai công ty A,B

b) Công ty nào có mức lương đồng đều hơn?

Phương pháp giải - Xem chi tiết Giải bài tập 2 trang 92 SGK Toán 12 tập 1 - Cánh diều 2

a) \({s^2} = \frac{{{n_1}.{{({x_1} - \overline x )}^2} + {n_2}{{({x_2} - \overline x )}^2} + ... + {n_p}{{({x_p} - \overline x )}^2}}}{n}\)

\(s = \sqrt {{s^2}} \)

b) Công ty nào có độ lệch chuẩn nhỏ hơn thì có mức lương đồng đều hơn

Lời giải chi tiết

Số trung bình cộng của mẫu số liệu ghép nhóm của công ty A là: \(\overline {{x_A}} = \frac{{15.12,5 + 18.17,5 + 10.22,5 + 10.27,5 + 5.32,5 + 2.37,5}}{{60}} = \frac{{62}}{3}\)

Phương sai của mẫu số liệu ghép nhóm của công ty A là:

\({s_A}^2 = \frac{{15.{{(12,5 - \frac{{62}}{3})}^2} + 18.{{(17,5 - \frac{{62}}{3})}^2} + 10.{{(22,5 - \frac{{62}}{3})}^2} + 10.{{(27,5 - \frac{{62}}{3})}^2} + 5.{{(32,5 - \frac{{62}}{3})}^2} + 2.{{(37,5 - \frac{{62}}{3})}^2}}}{{60}} \approx 49,14\)

Độ lệch chuẩn của mẫu số liệu ghép nhóm của công ty A là: \({s_A} = \sqrt {{s_A}^2} = \sqrt {49,13} \approx 7\)

Số trung bình cộng của mẫu số liệu ghép nhóm của công ty B là: \(\overline {{x_B}} = \frac{{25.12,5 + 15.17,5 + 7.22,5 + 5.27,5 + 5.32,5 + 3.37,5}}{{60}} = \frac{{229}}{{12}}\)

Phương sai của mẫu số liệu ghép nhóm của công ty B là:

\(\begin{array}{l}{s_B}^2 = \frac{{25.{{(12,5 - \frac{{229}}{{12}})}^2} + 15.{{(17,5 - \frac{{229}}{{12}})}^2} + 7.{{(22,5 - \frac{{229}}{{12}})}^2} + 5.{{(27,5 - \frac{{229}}{{12}})}^2} + 5.{{(32,5 - \frac{{229}}{{12}})}^2} + 3.{{(37,5 - \frac{{229}}{{12}})}^2}}}{{60}}\\ \approx 57,91\end{array}\)Độ lệch chuẩn của mẫu số liệu ghép nhóm của công ty B là: \({s_B} = \sqrt {{s_B}^2} = \sqrt {57,91} \approx 7,61\)

Nhận thấy độ lệch chuẩn của công ty A nhỏ hơn công ty B nên mức lương của công ty A đồng đều hơn

Giải Bài Tập 2 Trang 92 SGK Toán 12 Tập 1 Cánh Diều: Chi Tiết và Dễ Hiểu

Bài tập 2 trang 92 SGK Toán 12 tập 1 Cánh Diều thuộc chương trình học về giới hạn của hàm số. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học toán cao hơn. Việc nắm vững kiến thức và kỹ năng giải bài tập trong chương này sẽ giúp các em tự tin hơn khi làm bài kiểm tra và thi cử.

Nội dung bài tập 2 trang 92 SGK Toán 12 Tập 1 Cánh Diều

Bài tập 2 yêu cầu các em tính giới hạn của hàm số tại một điểm cho trước. Để giải bài tập này, các em cần nắm vững các định nghĩa và tính chất của giới hạn, cũng như các phương pháp tính giới hạn thường gặp như phương pháp chia, phương pháp nhân liên hợp, và sử dụng các giới hạn đặc biệt.

Lời giải chi tiết bài tập 2 trang 92 SGK Toán 12 Tập 1 Cánh Diều

Để giúp các em hiểu rõ hơn, chúng ta sẽ cùng nhau giải chi tiết bài tập 2 trang 92 SGK Toán 12 tập 1 Cánh Diều. (Ở đây sẽ là lời giải chi tiết cho từng ý của bài tập 2, bao gồm các bước giải, giải thích và kết luận. Ví dụ:)

Ý a: Tính lim_x→2 (x² - 4) / (x - 2)

Giải:

Ta có: (x² - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2)
Khi x ≠ 2, ta có: (x² - 4) / (x - 2) = x + 2
Vậy, lim_x→2 (x² - 4) / (x - 2) = lim_x→2 (x + 2) = 2 + 2 = 4

Ý b: Tính lim_x→1 (x³ - 1) / (x - 1)

Giải:

Ta có: (x³ - 1) / (x - 1) = (x - 1)(x² + x + 1) / (x - 1)
Khi x ≠ 1, ta có: (x³ - 1) / (x - 1) = x² + x + 1
Vậy, lim_x→1 (x³ - 1) / (x - 1) = lim_x→1 (x² + x + 1) = 1² + 1 + 1 = 3

Các phương pháp giải bài tập về giới hạn

Ngoài phương pháp phân tích đa thức như trên, các em có thể sử dụng các phương pháp sau để giải bài tập về giới hạn:

Phương pháp chia: Chia cả tử và mẫu cho xⁿ (n là số mũ lớn nhất của x).
Phương pháp nhân liên hợp: Nhân cả tử và mẫu với lượng liên hợp.
Sử dụng các giới hạn đặc biệt: lim_x→0 sinx/x = 1, lim_x→0 (1 - cosx)/x = 0,...

Lưu ý khi giải bài tập về giới hạn

Khi giải bài tập về giới hạn, các em cần lưu ý những điều sau:

Kiểm tra xem mẫu số có bằng 0 khi x tiến tới giá trị giới hạn hay không. Nếu mẫu số bằng 0, cần phải biến đổi biểu thức để khử dạng vô định.
Sử dụng đúng các định nghĩa và tính chất của giới hạn.
Kiểm tra lại kết quả sau khi giải xong.

Tổng kết

Hy vọng với lời giải chi tiết và các phương pháp giải bài tập về giới hạn được trình bày trên đây, các em sẽ tự tin hơn khi giải bài tập 2 trang 92 SGK Toán 12 tập 1 Cánh Diều và các bài tập tương tự. Chúc các em học tập tốt!

Mọi thắc mắc hoặc cần hỗ trợ thêm, đừng ngần ngại liên hệ với tusach.vn nhé!

Giải bài tập 2 trang 92 SGK Toán 12 tập 1 - Cánh diều