Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán 12 Cánh Diều
Tổng quan nội dung
Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị hàm số Toán 12 Cánh Diều
Chương trình Toán 12 Cánh Diều tập trung vào việc giúp học sinh nắm vững phương pháp khảo sát sự biến thiên và vẽ đồ thị của các hàm số thường gặp. Đây là một phần kiến thức quan trọng, không chỉ phục vụ cho kỳ thi THPT Quốc gia mà còn là nền tảng cho các kiến thức toán học nâng cao.
Tusach.vn xin giới thiệu tài liệu tổng hợp lý thuyết chi tiết, dễ hiểu, kèm theo các ví dụ minh họa và bài tập áp dụng để bạn có thể tự học hiệu quả.
1. Sơ đồ khảo sát hàm số Các bước khảo sát hàm số
1. Sơ đồ khảo sát hàm số
Các bước khảo sát hàm số
1. Tìm tập xác định của hàm số 2. Xét sự biến thiên của hàm số - Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số (nếu có) - Lập BBT của hàm số bao gồm: Tính đạo hàm của hàm số, xét dấu đạo hàm, xét chiều biến thiên và tìm cực trị của hàm số (nếu có), điền các kết quả vào bảng 3. Vẽ đồ thị của hàm số - Vẽ các đường tiệm cận (nếu có) - Xác định các điểm đặc biệt của đồ thị: cực trị, giao điểm của đồ thị với các trục tọa độ (trong trường hợp đơn giản), … - Nhận xét về đặc điểm của đồ thị: chỉ ra tâm đối xứng, trục đối xứng (nếu có) |
2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc ba
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - {x^3} + 3{x^2} - 4\)
1. Tập xác định của hàm số: R
2. Sự biến thiên:
Ta có: \(y' = - 3{x^2} + 6x\). Vậy y’ = 0 khi x = 0 hoặc x = 2
Trên khoảng \(\left( {0;2} \right)\), y’ > 0 nên hàm số đồng biến. Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\), y’ < 0 nên hàm số nghịch biến trên mỗi khoảng đó
Hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu \({y_{CT}} = - 4\). Hàm số đạt cực đại tại x = 2, giá trị cực đại
Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty \)
BBT:

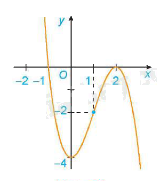
4. Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0;4} \right)\)
Ta có: y = 0 \( \Leftrightarrow \)x = -1 hoặc x = 2. Do đó giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( { - 1;0} \right)\) và \(\left( {2;0} \right)\)
Đồ thị hàm số có tâm đối xứng là điểm \(\left( {1; - 2} \right)\)
3. Khảo sát và vẽ đồ thị hàm số phân thức hữu tỷ
a) Hàm số phân thức \(y = \frac{{ax + b}}{{cx + d}}(c \ne 0,ad - bc \ne 0)\)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{x + 1}}{{x - 2}}\)
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên:
Ta có: \(y' = - \frac{3}{{{{(x - 2)}^2}}} < 0\) với mọi \(x \ne 2\)
Hàm số nghịch biến trên từng khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\)
Hàm số không có cực trị
Tiệm cận: \(\mathop {\lim }\limits_{x \to - \infty } y = 1;\mathop {\lim }\limits_{x \to + \infty } - \infty = 1\)
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \)
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận ngang là y = 1
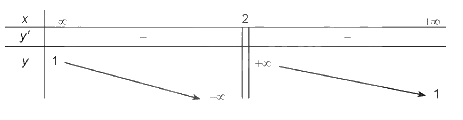
BBT:
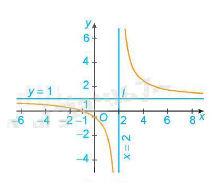
4. Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0; - \frac{1}{2}} \right)\)
Giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( { - 1;0} \right)\)
Đồ thị hàm số nhận giao điểm I \(\left( {2;1} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng
b) Hàm số phân thức \(y = \frac{{a{x^2} + bx + c}}{{px + q}}(a \ne 0,p \ne 0)\)(đa thức tử không chia hết cho đa thức mẫu)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{{x^2} - x - 1}}{{x - 2}}\)
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên: Viết \(y = x + 1 + \frac{1}{{x - 2}}\)
Ta có: \(y' = 1 - \frac{1}{{{{(x - 2)}^2}}} = \frac{{{x^2} - 4x + 3}}{{{{(x - 2)}^2}}}\) . Vậy y’ = 0 \( \Leftrightarrow \) x = 1 hoặc x = 3
Trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\), y’ > 0 nên hàm số đồng biến trên từng khoảng này
Trên các khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\), y’ < 0 nên hàm số nghịch biến trên từng khoảng này
Hàm số đạt cực đại tại x = 1 với ; hàm số đạt cực tiểu tại x = 3 với \({y_{CT}} = 5\)
\(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty \)
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 2}} = 0\); \(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 2}} = 0\)
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận xiên là y = x+1
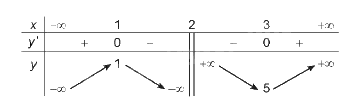
BBT:
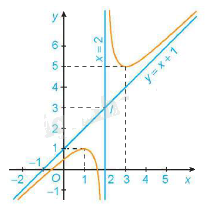
3. Đồ thị:
Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0;\frac{1}{2}} \right)\)
Ta có: \(y = 0 \Leftrightarrow x = \frac{{1 - \sqrt 5 }}{2};x = \frac{{1 + \sqrt 5 }}{2}\). Do đó giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( {\frac{{1 - \sqrt 5 }}{2};0} \right);\left( {\frac{{1 + \sqrt 5 }}{2};0} \right)\)
Đồ thị hàm số nhận giao điểm I \(\left( {2;3} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng
4. Ứng dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn
Ví dụ: Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức \(f(t) = \frac{{26t + 10}}{{t + 5}}\) (f(t) được tính bằng nghìn người)
a) Tính số dân của thị trấn vào năm 2022
b) Xem y = f(t) là một hàm số xác định trên nửa khoảng \(\left[ {0; + \infty } \right)\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số f(t)
c) Đạo hàm của hàm số y = f(t) biểu thị tốc độ tăng dân số của thị trấn (tính bằng nghìn người/năm)
- Tính tốc độ tăng dân số vào năm 2022 của thị trấn đó
- Vào năm nào thì tốc độ tăng dân số là 0,192 nghìn người/năm ?
Giải:
a) Ta có: \(f(52) = \frac{{26.52 + 10}}{{52 + 5}} = \frac{{1362}}{{57}} \approx 23,895\) (nghìn người)
Vậy số dân của thị trấn vào năm 2022 khoảng 23895 nghìn người
b) 1) Sự biến thiên
- Giới hạn tại vô cực và đường tiệm cận ngang:
\(\mathop {\lim }\limits_{t \to + \infty } f(t) = 26\). Do đó, đường thẳng y = 26 là tiệm cận ngang của đồ thị hàm số.
- BBT:
\(f'(t) = \frac{{120}}{{{{(t + 5)}^2}}} > 0\) với mọi \(t \ge 0\)
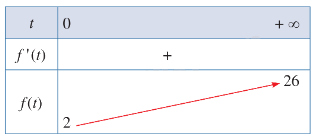
Hàm số đồng biến trên nửa khoảng \(\left[ {0; + \infty } \right)\).
Hàm số không có cực trị
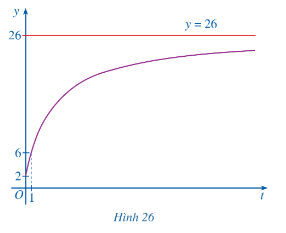
2) Đồ thị
- Giao điểm của đồ thị với trục tung (0;2)
- Đồ thị hàm số đi qua điểm (1;6). Vậy đồ thị hàm số \(y = f(t) = \frac{{26t + 10}}{{t + 5}}\), \(t \ge 0\) được cho ở hình vẽ sau
c)
- Tốc độ tăng dân số vào năm 2022 của thị trấn đó là:
\(f'(52) = \frac{{120}}{{{{(52 + 5)}^2}}} = \frac{{40}}{{1083}}\)
- Ta có:
\(f'(t) = 0,192 \Leftrightarrow \frac{{120}}{{{{(t + 5)}^2}}} = 0,192 \Leftrightarrow {(t + 5)^2} = 625 \Leftrightarrow t = 20\) (do \(t \ge 0\))
Vậy vào năm 1990, tốc độ tăng dân số là 0,192 nghìn người/năm
Lý Thuyết Khảo Sát Sự Biến Thiên và Vẽ Đồ Thị Hàm Số Toán 12 Cánh Diều: Tổng Quan
Khảo sát sự biến thiên và vẽ đồ thị hàm số là một trong những chủ đề quan trọng bậc nhất trong chương trình Toán 12, đặc biệt là theo sách Cánh Diều. Nắm vững kiến thức này không chỉ giúp học sinh đạt điểm cao trong các kỳ thi mà còn rèn luyện tư duy logic và khả năng phân tích toán học.
1. Các Bước Khảo Sát Sự Biến Thiên của Hàm Số
- Xác định tập xác định: Tìm miền xác định của hàm số.
- Tính đạo hàm cấp nhất: Tính f'(x) và tìm các điểm tới hạn (điểm mà f'(x) = 0 hoặc không xác định).
- Xác định khoảng đơn điệu: Xét dấu f'(x) trên từng khoảng xác định để xác định khoảng hàm số đồng biến, nghịch biến.
- Tìm cực trị: Sử dụng đạo hàm cấp nhất để xác định các điểm cực đại, cực tiểu.
- Tính đạo hàm cấp hai: Tính f''(x) và tìm các điểm uốn (điểm mà f''(x) = 0 hoặc không xác định).
- Xác định khoảng lồi, lõm: Xét dấu f''(x) trên từng khoảng xác định để xác định khoảng hàm số lồi, lõm.
- Tìm tiệm cận: Xác định các tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có).
- Lập bảng biến thiên: Tổng hợp các kết quả trên vào bảng biến thiên.
- Vẽ đồ thị: Dựa vào bảng biến thiên và các điểm đặc biệt để vẽ đồ thị hàm số.
2. Các Loại Hàm Số Thường Gặp và Phương Pháp Khảo Sát
- Hàm số bậc ba: Chú trọng tìm điểm uốn và xét tính đối xứng.
- Hàm số hữu tỉ: Chú trọng tìm tiệm cận và xét giới hạn tại vô cùng.
- Hàm số lượng giác: Chú trọng tính chu kỳ và xét các điểm đặc biệt.
- Hàm số mũ và logarit: Chú trọng xét tính đơn điệu và giới hạn.
3. Ví dụ Minh Họa: Khảo sát hàm số y = x3 - 3x2 + 2
Bước 1: Tập xác định: D = ℝ
Bước 2: Đạo hàm cấp nhất: y' = 3x2 - 6x
Bước 3: Giải phương trình y' = 0: 3x2 - 6x = 0 => x = 0 hoặc x = 2
Bước 4: Bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Bước 5: Kết luận: Hàm số đồng biến trên (-∞; 0) và (2; +∞), nghịch biến trên (0; 2). Hàm số đạt cực đại tại x = 0, ycđ = 2 và cực tiểu tại x = 2, yct = -2.
4. Mẹo Học Tập và Luyện Tập Hiệu Quả
- Nắm vững lý thuyết: Hiểu rõ các khái niệm và định lý liên quan.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài.
- Sử dụng công cụ hỗ trợ: Sử dụng máy tính cầm tay hoặc các phần mềm vẽ đồ thị để kiểm tra kết quả.
- Học hỏi từ các nguồn tài liệu: Tham khảo sách giáo khoa, sách tham khảo, bài giảng trực tuyến.
Tusach.vn hy vọng với những kiến thức và hướng dẫn trên, bạn sẽ tự tin chinh phục phần Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị hàm số Toán 12 Cánh Diều. Chúc bạn học tập tốt!