Giải bài tập 2 trang 20 SGK Toán 12 tập 1 - Cánh diều
Tổng quan nội dung
Giải bài tập 2 trang 20 SGK Toán 12 tập 1 - Cánh diều
Chào mừng bạn đến với tusach.vn! Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài tập 2 trang 20 SGK Toán 12 tập 1 - Cánh diều. Chúng tôi hy vọng sẽ giúp bạn hiểu rõ hơn về kiến thức và kỹ năng cần thiết để giải quyết các bài toán trong chương trình học.
Với đội ngũ giáo viên giàu kinh nghiệm, tusach.vn cam kết mang đến cho bạn những giải pháp học tập hiệu quả nhất.
Tìm giá trị lớn nhất của mỗi hàm số sau: a) (fleft( x right) = frac{4}{{1 + {x^2}}}). b) (fleft( x right) = x - frac{3}{x}) trên nửa khoảng ((0;3]).
Đề bài
Tìm giá trị lớn nhất của mỗi hàm số sau:
a) \(f\left( x \right) = \frac{4}{{1 + {x^2}}}\).
b) \(f\left( x \right) = x - \frac{3}{x}\) trên nửa khoảng \((0;3]\).
Phương pháp giải - Xem chi tiết
B1: Tìm các điểm \({x_1},{x_2},...,{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
B2: Tính \(f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),f\left( a \right),f\left( b \right)\).
B3: So sánh các giá trị tìm được ở bước 2 và kết luận.
Lời giải chi tiết
a) Tập xác định \(D = R\).
Ta có: \(f'\left( x \right) = \frac{{8x}}{{{{\left( {1 + {x^2}} \right)}^2}}}\).
Nhận xét \(f'\left( x \right) = \frac{{ - 8x}}{{{{\left( {1 + {x^2}} \right)}^2}}} = 0 \Leftrightarrow x = 0\).
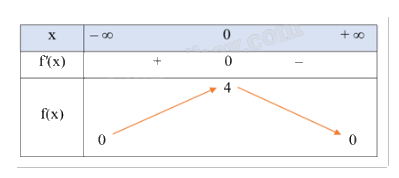
Vậy giá trị lớn nhất của hàm số bằng 4 khi \(x = 0\).
b) Ta có: \(f'\left( x \right) = 1 + \frac{3}{{{x^2}}}\).
Nhận xét \(f'\left( x \right) > 0\forall x \in (0;3]\). Hàm số đồng biến trên (0;3].
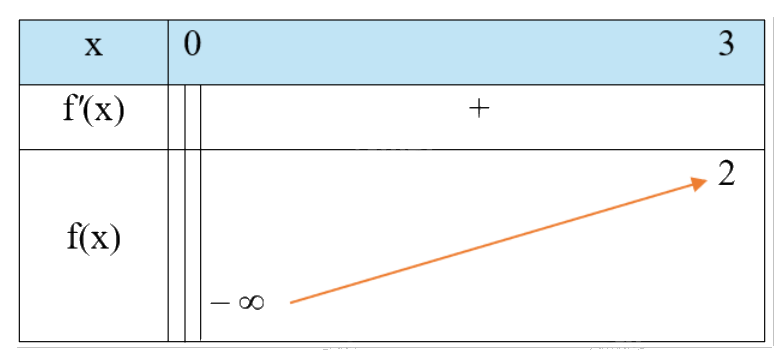
Vậy giá trị lớn nhất của hàm số bằng 2 khi \(x = 3\).
Giải bài tập 2 trang 20 SGK Toán 12 tập 1 - Cánh diều: Hướng dẫn chi tiết và dễ hiểu
Bài tập 2 trang 20 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về Hàm số bậc hai. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học nâng cao hơn. Bài tập này yêu cầu học sinh vận dụng kiến thức về định nghĩa hàm số, tập xác định, tập giá trị, tính đơn điệu và cực trị của hàm số bậc hai để giải quyết.
Nội dung bài tập 2 trang 20 SGK Toán 12 tập 1 - Cánh diều
Bài tập 2 thường bao gồm các dạng câu hỏi sau:
- Xác định hàm số bậc hai dựa vào các thông tin cho trước.
- Tìm tập xác định và tập giá trị của hàm số.
- Xác định khoảng đồng biến, nghịch biến của hàm số.
- Tìm tọa độ đỉnh, trục đối xứng và điểm cắt trục tung của đồ thị hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết bài tập 2 trang 20 SGK Toán 12 tập 1 - Cánh diều
Để giải quyết bài tập này một cách hiệu quả, bạn cần:
- Nắm vững định nghĩa hàm số bậc hai: Hàm số bậc hai có dạng y = ax2 + bx + c, với a ≠ 0.
- Hiểu rõ các yếu tố ảnh hưởng đến đồ thị hàm số: Hệ số a quyết định chiều mở của parabol (lên trên nếu a > 0, xuống dưới nếu a < 0).
- Sử dụng công thức tính tọa độ đỉnh: Tọa độ đỉnh của parabol là (-b/2a, (4ac - b2)/4a).
- Vận dụng các kiến thức về tính đơn điệu và cực trị: Hàm số bậc hai có tính đơn điệu trên các khoảng xác định.
Dưới đây là ví dụ minh họa lời giải cho một dạng bài tập thường gặp:
Ví dụ: Cho hàm số y = x2 - 4x + 3. Hãy tìm tọa độ đỉnh và vẽ đồ thị hàm số.
Lời giải:
- a = 1, b = -4, c = 3
- Tọa độ đỉnh: xđỉnh = -b/2a = -(-4)/(2*1) = 2; yđỉnh = (4*1*3 - (-4)2)/4*1 = -1. Vậy tọa độ đỉnh là (2, -1).
- Trục đối xứng: x = 2
- Điểm cắt trục tung: (0, 3)
- Điểm cắt trục hoành: Giải phương trình x2 - 4x + 3 = 0, ta được x1 = 1, x2 = 3. Vậy điểm cắt trục hoành là (1, 0) và (3, 0).
Dựa vào các thông tin trên, bạn có thể vẽ được đồ thị hàm số y = x2 - 4x + 3.
Mẹo giải bài tập hiệu quả
Để giải bài tập 2 trang 20 SGK Toán 12 tập 1 - Cánh diều một cách nhanh chóng và chính xác, bạn nên:
- Đọc kỹ đề bài và xác định rõ yêu cầu.
- Sử dụng các công thức và định lý liên quan một cách linh hoạt.
- Kiểm tra lại kết quả sau khi giải xong.
- Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn đồng hành cùng bạn trong quá trình học tập. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các mẹo giải bài tập hiệu quả. Hãy truy cập tusach.vn để khám phá thêm nhiều kiến thức hữu ích và đạt kết quả tốt nhất trong học tập!
Chúc bạn học tốt!