Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều
SGK Toán 12 - Cánh diều
Giải Toán 12 tập 1 - Cánh diều
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Bài 1. Tính đơn điệu của hàm số

Giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều

Giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu sắc kiến thức và tự tin làm bài tập.

Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp tài liệu học tập chất lượng và hỗ trợ tối đa.

Tìm các khoảng đơn điệu của hàm số sau: a) \(y = - {x^3} + 2{x^2} - 3\) b) \(y = {x^4} + 2{x^2} + 5\) c) \(y = \frac{{3x + 1}}{{2 - x}}\) d) \(y = \frac{{{x^2} - 2x}}{{x + 1}}\)

Đề bài

Tìm các khoảng đơn điệu của hàm số sau:a) \(y = - {x^3} + 2{x^2} - 3\)

b) \(y = {x^4} + 2{x^2} + 5\)

c) \(y = \frac{{3x + 1}}{{2 - x}}\)

d) \(y = \frac{{{x^2} - 2x}}{{x + 1}}\)

Phương pháp giải - Xem chi tiếtGiải bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều 1

B1: Tìm tập xác định của hàm số.

B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.

B3: Lập bảng biến thiên của hàm số.

B4: Dựa vào bảng biến thiên để kết luận.

Lời giải chi tiết

a) Tập xác định: \(D = \mathbb{R}\).

Ta có: \(y' = - 3{x^2} + 4x\).

Nhận xét \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{4}{3}\end{array} \right.\)

Ta có bảng biến thiên sau:

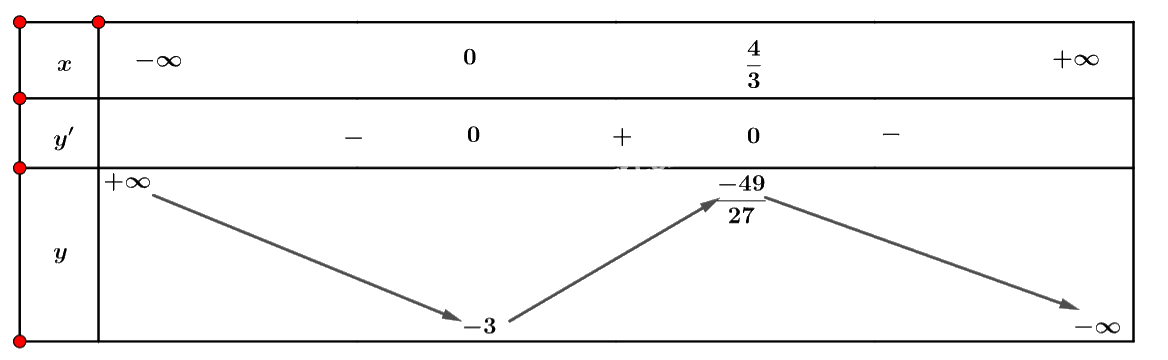
Giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều 2

Vậy hàm số đồng biến trên khoảng \(\left( {0;\frac{4}{3}} \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {\frac{4}{3}; + \infty } \right)\).

b) Tập xác định: \(D = \mathbb{R}\).

Ta có: \(y' = 4{x^3} + 4x\).

Nhận xét \(y' = 0 \Leftrightarrow x = 0.\)

Ta có bảng biến thiên sau:

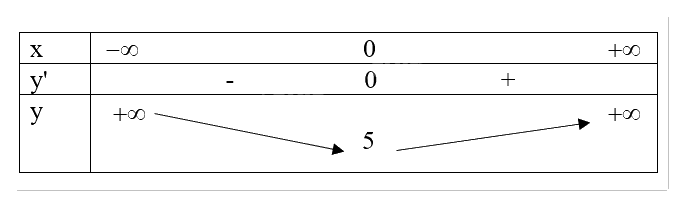
Giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều 3

Vậy hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; 0} \right)\).

c) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).

Ta có: \(y' = \frac{5}{{{{\left( {2 - x} \right)}^2}}}\).

Nhận xét \(y' > 0{\rm{ }}\forall x \in D\)

Ta có bảng biến thiên sau:

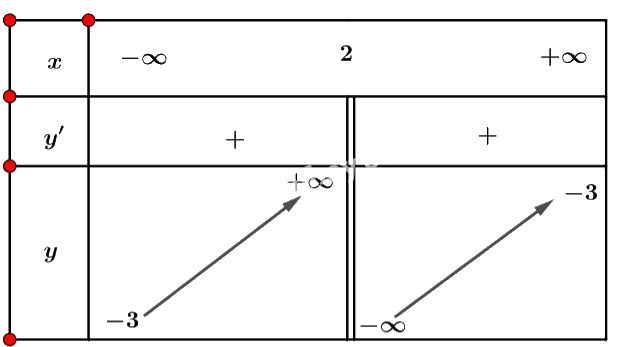
Giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều 4

Vậy hàm số đồng biến trên khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).

d) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).

Ta có: \(y' = \frac{{\left( {2x - 2} \right)\left( {x + 1} \right) - {x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2x - 2}}{{{{\left( {x + 1} \right)}^2}}}\).

Nhận xét \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1 + \sqrt 3 \\x = - 1 - \sqrt 3 \end{array} \right.\).

Ta có bảng biến thiên sau:

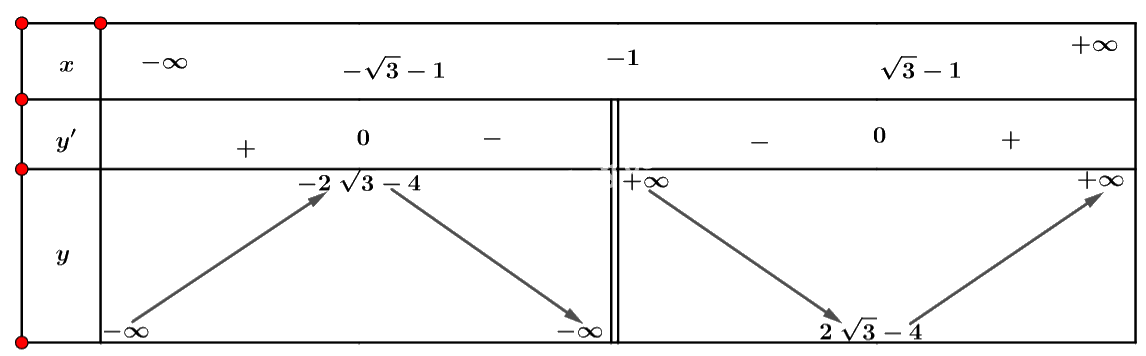
Giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều 5

Vậy hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1 - \sqrt 3 } \right)\) và \(\left( { - 1 + \sqrt 3 ; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - 1 - \sqrt 3 ; - 1} \right)\) và \(\left( { - 1; - 1 + \sqrt 3 } \right)\).

Giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều: Hướng dẫn chi tiết và dễ hiểu

Bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về giới hạn của hàm số. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học nâng cao hơn. Việc nắm vững lý thuyết và phương pháp giải bài tập là điều cần thiết để đạt kết quả tốt trong môn Toán.

Nội dung bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều

Bài tập 3 yêu cầu tính các giới hạn sau:

  1. lim (x→2) (x^2 - 3x + 2) / (x - 2)
  2. lim (x→-1) (x^3 + 1) / (x + 1)
  3. lim (x→0) (√(x+1) - 1) / x

Hướng dẫn giải chi tiết

Để giải các bài tập này, chúng ta cần áp dụng các phương pháp tính giới hạn sau:

  • Phân tích thành nhân tử: Đối với các biểu thức có dạng phân thức, ta có thể phân tích tử và mẫu thành nhân tử để rút gọn biểu thức, từ đó tính giới hạn.
  • Nhân liên hợp: Đối với các biểu thức chứa căn thức, ta có thể nhân cả tử và mẫu với liên hợp của biểu thức chứa căn thức để khử căn thức, từ đó tính giới hạn.
  • Quy tắc L'Hopital: Nếu giới hạn có dạng 0/0 hoặc ∞/∞, ta có thể áp dụng quy tắc L'Hopital để tính giới hạn.

Giải bài tập 3.1: lim (x→2) (x^2 - 3x + 2) / (x - 2)

Ta có: x^2 - 3x + 2 = (x - 1)(x - 2). Do đó:

lim (x→2) (x^2 - 3x + 2) / (x - 2) = lim (x→2) (x - 1)(x - 2) / (x - 2) = lim (x→2) (x - 1) = 2 - 1 = 1

Giải bài tập 3.2: lim (x→-1) (x^3 + 1) / (x + 1)

Ta có: x^3 + 1 = (x + 1)(x^2 - x + 1). Do đó:

lim (x→-1) (x^3 + 1) / (x + 1) = lim (x→-1) (x + 1)(x^2 - x + 1) / (x + 1) = lim (x→-1) (x^2 - x + 1) = (-1)^2 - (-1) + 1 = 1 + 1 + 1 = 3

Giải bài tập 3.3: lim (x→0) (√(x+1) - 1) / x

Ta nhân cả tử và mẫu với liên hợp của tử số là √(x+1) + 1:

lim (x→0) (√(x+1) - 1) / x = lim (x→0) [(√(x+1) - 1)(√(x+1) + 1)] / [x(√(x+1) + 1)] = lim (x→0) (x+1 - 1) / [x(√(x+1) + 1)] = lim (x→0) x / [x(√(x+1) + 1)] = lim (x→0) 1 / (√(x+1) + 1) = 1 / (√(0+1) + 1) = 1 / (1 + 1) = 1/2

Kết luận

Vậy, kết quả của các bài tập là:

  • lim (x→2) (x^2 - 3x + 2) / (x - 2) = 1
  • lim (x→-1) (x^3 + 1) / (x + 1) = 3
  • lim (x→0) (√(x+1) - 1) / x = 1/2

Hy vọng bài giải này sẽ giúp các em hiểu rõ hơn về cách tính giới hạn và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!

Tusach.vn - Đồng hành cùng bạn trên con đường chinh phục tri thức.

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN