Giải bài tập 9 trang 47 SGK Toán 12 tập 1 - Cánh diều
Tổng quan nội dung
Giải bài tập 9 trang 47 SGK Toán 12 tập 1 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 9 trang 47 SGK Toán 12 tập 1 - Cánh Diều. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em tự tin hơn trong quá trình học tập môn Toán.
tusach.vn luôn đồng hành cùng các em học sinh, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau a,(y = {x^3} - 3{x^2} + 2) (b,;y = - {x^3} + 3{x^2} - 6x) (c,y = frac{{3x - 2}}{{x - 2}}) (d,y = frac{x}{{2x + 3}}) (e,y = frac{{{x^2} + 2x + 4}}{x}) (g,y = frac{{{x^2} + 4x + 3}}{{x + 2}};)
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau
a,\(y = {x^3} - 3{x^2} + 2\)
\(b,\;y = - {x^3} + 3{x^2} - 6x\)
\(c,y = \frac{{3x - 2}}{{x - 2}}\)
\(d,y = \frac{x}{{2x + 3}}\)
\(e,y = \frac{{{x^2} + 2x + 4}}{x}\)
\(g,y = \frac{{{x^2} + 4x + 3}}{{x + 2}}\;\)
Phương pháp giải - Xem chi tiết
Tìm tập xác định
Vẽ bảng biến thiên
Vẽ đồ thị
Lời giải chi tiết
\(a,\;y = {x^3} - 3{x^2} + 2\)
TXD : R
\(y' = 3{x^2} - 6x\)
Cho y= 0 => \(\left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\)
Bảng biến thiên:
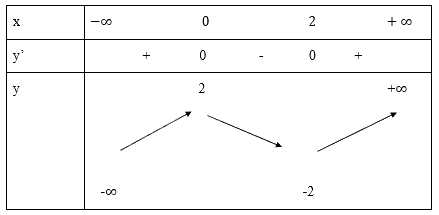
Đồ thị hàm số:
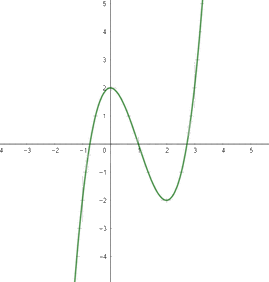
Hàm số đồng biến trong khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\)
Hàm số nghịch biến trong khoảng (0;2)
\(\;b,\;y = - {x^3} + 3{x^2} - 6x\)
TXD: R
\(y' = \; - 3{x^2} + 6x - 6\)
Bảng biến thiên:
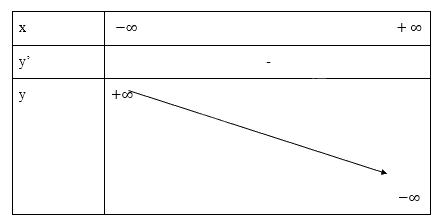
Đồ thị hàm số
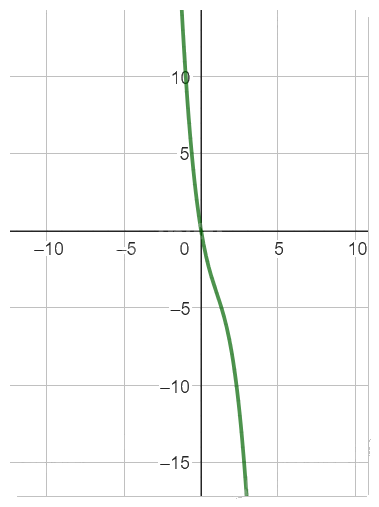
Hàm số nghịch biến trên R
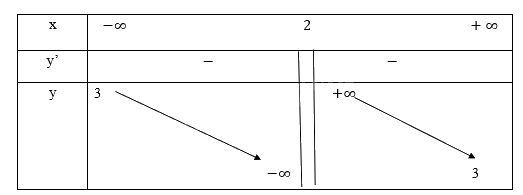
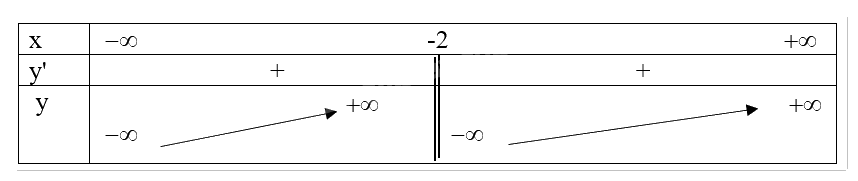
\(c,y = \frac{{3x - 2}}{{x - 2}}\)
TXD: R/2
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x - 2}} = 3 = > TCN\;y = 3\)
\(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{3x - 2}}{{x - 2}} = - \infty \)
Bảng biến thiên:
Đồ thị hàm số:
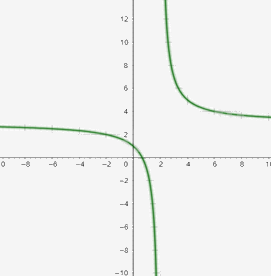
Hàm số nghịch biến trên khoảng R
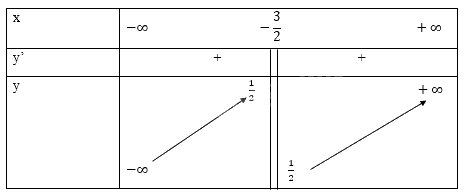
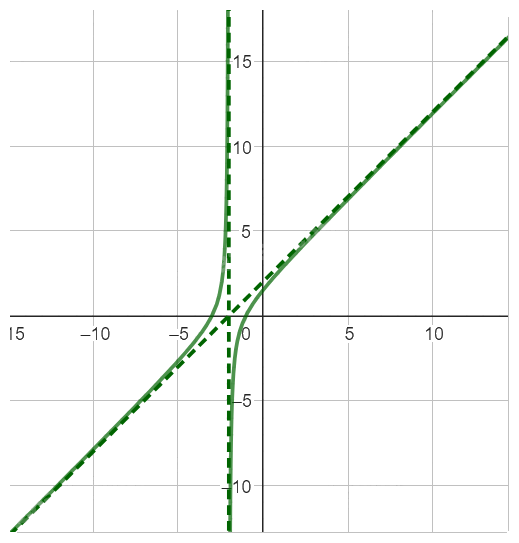
\(d,y = \frac{x}{{2x + 3}}\)
TXD: R \ {\( - \frac{3}{2}\)}
TCN \(y = \frac{1}{2}\)
TCD \(x = - \frac{3}{2}\)
Bảng biến thiên
Đồ thị hàm số:
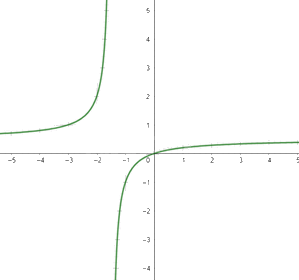
\(e,y = \frac{{{x^2} + 2x + 4}}{x}\)
\(TXD:\mathbb{R}\backslash \{ 0\} \)
TCD: x = 0.
Không có tiệm cận ngang.
Có thể viết hàm số đã cho dưới dạng: \(y = \frac{{{x^2} + 4x + 3}}{{x + 2}} = x + 2 + \frac{4}{x}\), suy ra:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{4}{x} = 0.\\\mathop {\lim }\limits_{x \to - \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{4}{x} = 0.\end{array}\)
Do đó, đồ thị hàm số có \(y = x + 2\) là tiệm cận xiên.
\(y' = \frac{{\left( {2x + 2} \right)x - \left( {{x^2} + 2x + 4} \right)}}{{{x^2}}} = \frac{{{x^2} - 4}}{{{x^2}}}\).
Cho y’=0 => x=\( \pm 2\).
Bảng biến thiên:
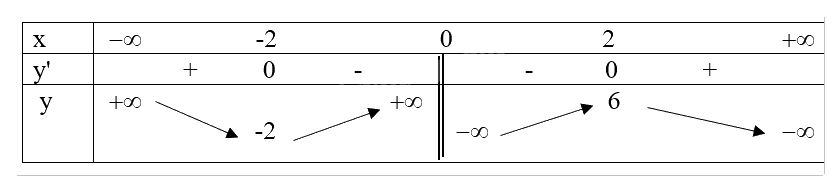
Đồ thị hàm số:
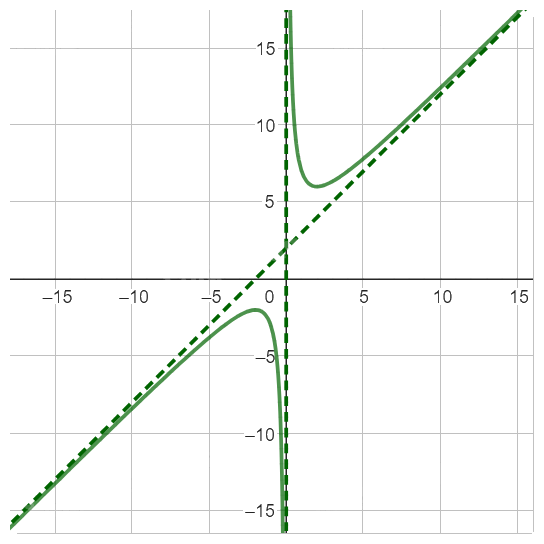
g, \(y = \frac{{{x^2} + 4x + 3}}{{x + 2}}\)
TXD: \(\mathbb{R}\backslash \{ - 2\} \). \[\]
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \). Đồ thị àm số không có tiệm cận ngang.
\(\mathop {\lim }\limits_{x \to - {2^ + }} y = - \infty ,\mathop {\lim }\limits_{x \to - {2^ - }} y = + \infty \). Đồ thị hàm số có \(x = - 2\) là tiệm cận đứng.
Có thể viết hàm số đã cho dưới dạng: \(y = \frac{{{x^2} + 4x + 3}}{{x + 2}} = x + 2 - \frac{1}{{x + 2}}\), suy ra:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1}}{{x + 2}} = 0.\\\mathop {\lim }\limits_{x \to - \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 1}}{{x + 2}} = 0.\end{array}\)
Do đó, đồ thị hàm số có \(y = x + 2\) là tiệm cận xiên.
Bảng biến thiên:
Đồ thị hàm số:
Giải bài tập 9 trang 47 SGK Toán 12 tập 1 - Cánh Diều: Tổng quan và Phương pháp giải
Bài tập 9 trang 47 SGK Toán 12 tập 1 - Cánh Diều thuộc chương trình học về Hàm số bậc hai. Đây là một dạng bài tập quan trọng, thường xuyên xuất hiện trong các đề thi. Để giải quyết bài tập này một cách hiệu quả, các em cần nắm vững kiến thức về:
- Định nghĩa hàm số bậc hai.
- Các dạng biểu diễn của hàm số bậc hai (dạng tổng quát, dạng chuẩn).
- Đồ thị hàm số bậc hai (đỉnh, trục đối xứng, giao điểm với các trục tọa độ).
- Các tính chất của hàm số bậc hai (tính đơn điệu, giá trị lớn nhất/nhỏ nhất).
Nội dung bài tập 9 trang 47 SGK Toán 12 tập 1 - Cánh Diều
Bài tập 9 thường yêu cầu các em thực hiện các thao tác sau:
- Xác định các hệ số a, b, c của hàm số bậc hai.
- Tìm tọa độ đỉnh của parabol.
- Vẽ đồ thị hàm số.
- Tìm khoảng đồng biến, nghịch biến của hàm số.
- Tìm giá trị lớn nhất/nhỏ nhất của hàm số.
- Giải các bài toán liên quan đến ứng dụng của hàm số bậc hai.
Lời giải chi tiết bài tập 9 trang 47 SGK Toán 12 tập 1 - Cánh Diều
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập yêu cầu:
"Tìm tọa độ đỉnh và vẽ đồ thị hàm số y = x2 - 4x + 3"
Bước 1: Xác định các hệ số a, b, c
Trong hàm số y = x2 - 4x + 3, ta có a = 1, b = -4, c = 3.
Bước 2: Tính tọa độ đỉnh của parabol
Tọa độ đỉnh của parabol là I(x0, y0), với:
- x0 = -b / 2a = -(-4) / (2 * 1) = 2
- y0 = f(x0) = f(2) = 22 - 4 * 2 + 3 = -1
Vậy tọa độ đỉnh của parabol là I(2, -1).
Bước 3: Vẽ đồ thị hàm số
Để vẽ đồ thị hàm số, ta cần xác định thêm một số điểm thuộc parabol. Ví dụ:
| x | y |
|---|---|
| 0 | 3 |
| 1 | 0 |
| 3 | 0 |
| 4 | 3 |
Sau khi xác định được các điểm, ta vẽ parabol đi qua các điểm này và có đỉnh là I(2, -1).
Lưu ý khi giải bài tập về hàm số bậc hai
- Luôn kiểm tra điều kiện xác định của hàm số.
- Sử dụng các công thức và tính chất của hàm số bậc hai một cách chính xác.
- Vẽ đồ thị hàm số để hiểu rõ hơn về tính chất của hàm số.
- Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải bài tập.
Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín
tusach.vn tự hào là một trong những website cung cấp tài liệu học tập Toán 12 uy tín và chất lượng nhất hiện nay. Chúng tôi cung cấp đầy đủ các tài liệu sau:
- Giải bài tập SGK Toán 12 tập 1, tập 2.
- Giải bài tập VBT Toán 12 tập 1, tập 2.
- Đề thi thử Toán 12.
- Bài giảng Toán 12.
- Các tài liệu ôn thi THPT Quốc gia môn Toán.
Hãy truy cập tusach.vn ngay hôm nay để khám phá kho tài liệu học tập Toán 12 phong phú và hữu ích!