Giải bài tập 5 trang 40 SGK Toán 12 tập 2 - Cánh diều

Chào mừng bạn đến với tusach.vn! Chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho bài tập 5 trang 40 SGK Toán 12 tập 2 - Cánh diều. Bài viết này sẽ giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.

Cho đồ thị hàm số (y = frac{1}{x}) và khối tròn xoay như Hình 31 a) Hình phẳng được giới hạn bởi các đường nào để khi xoay quanh trục Ox ta được khối tròn xoay như Hình 31? b) Tính thể tích khối tròn xoay đó

Đề bài

Cho đồ thị hàm số \(y = \frac{1}{x}\) và khối tròn xoay như Hình 31.

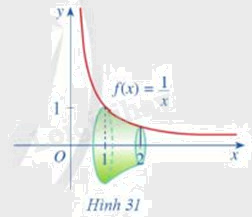
Giải bài tập 5 trang 40 SGK Toán 12 tập 2 - Cánh diều 1

a) Hình phẳng được giới hạn bởi các đường nào để khi xoay quanh trục Ox ta được khối tròn xoay như Hình 31?

b) Tính thể tích khối tròn xoay đó.

Phương pháp giải - Xem chi tiết Giải bài tập 5 trang 40 SGK Toán 12 tập 2 - Cánh diều 2

a) Quan sát hình vẽ.

b) Cho hàm số y = f(x) liên tục, không âm trên đoạn [a;b]. Hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b quay quanh trục Ox tạo thành một khối tròn xoay có thể tích bằng \(V = \pi \int\limits_a^b {{{[f(x)]}^2}dx} \).

Lời giải chi tiết

a) Hình phẳng đó được giới hạn bởi đồ thị hàm số \(y = \frac{1}{x}\), trục Ox, đường thẳng x = 1 và x = 2.

b) Thể tích khối tròn xoay đó là:

\(V = \pi \int\limits_1^2 {{{\left( {\frac{1}{x}} \right)}^2}dx} = \pi \int\limits_1^2 {{x^{ - 2}}dx} = \pi \frac{{{x^{ - 2 + 1}}}}{{ - 2 + 1}}\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. = - \pi {x^{ - 1}}\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. = \frac{{ - \pi }}{x}\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right. = \frac{{ - \pi }}{2} - \frac{{ - \pi }}{1} = \frac{\pi }{2}\).

Giải bài tập 5 trang 40 SGK Toán 12 tập 2 - Cánh diều: Tổng quan và Phương pháp giải

Bài tập 5 trang 40 SGK Toán 12 tập 2 - Cánh diều thuộc chương trình học Toán 12, tập trung vào kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh vận dụng các công thức đạo hàm cơ bản, quy tắc tính đạo hàm của hàm hợp, và các phương pháp giải phương trình, bất phương trình để tìm ra nghiệm và kết luận về tính đơn điệu, cực trị của hàm số.

Nội dung chi tiết bài tập 5 trang 40

Để giải quyết bài tập này một cách hiệu quả, bạn cần:

Xác định đúng yêu cầu của bài toán: Đọc kỹ đề bài để hiểu rõ hàm số cần khảo sát, khoảng xác định, và các yêu cầu cụ thể (ví dụ: tìm cực trị, khoảng đơn điệu, giá trị lớn nhất, giá trị nhỏ nhất).
Tính đạo hàm cấp một (y'): Sử dụng các quy tắc đạo hàm để tính đạo hàm của hàm số.
Tìm điểm tới hạn: Giải phương trình y' = 0 để tìm các điểm mà đạo hàm bằng không. Đây là các điểm nghi ngờ có cực trị hoặc điểm đổi hướng của hàm số.
Khảo sát dấu của đạo hàm cấp một: Lập bảng xét dấu của y' trên các khoảng xác định của hàm số. Dựa vào dấu của y', ta có thể kết luận về khoảng đồng biến, nghịch biến của hàm số.
Tìm cực trị của hàm số: Sử dụng tiêu chuẩn xét cực trị (ví dụ: tiêu chuẩn dấu của đạo hàm cấp một hoặc đạo hàm cấp hai) để xác định các điểm cực đại, cực tiểu của hàm số.
Tính đạo hàm cấp hai (y''): Tính đạo hàm cấp hai của hàm số.
Tìm điểm uốn: Giải phương trình y'' = 0 để tìm các điểm uốn của hàm số.
Khảo sát tính lồi, lõm của hàm số: Lập bảng xét dấu của y'' trên các khoảng xác định của hàm số. Dựa vào dấu của y'', ta có thể kết luận về khoảng lồi, lõm của hàm số.

Lời giải chi tiết bài tập 5 trang 40 (Ví dụ)

Giả sử bài tập 5 yêu cầu khảo sát hàm số y = x³ - 3x² + 2.

Bước 1: Tính đạo hàm cấp một: y' = 3x² - 6x

Bước 2: Tìm điểm tới hạn: 3x² - 6x = 0 => x = 0 hoặc x = 2

Bước 3: Khảo sát dấu của đạo hàm cấp một:

Khoảng	x < 0	0 < x < 2	x > 2
y'	+	-	+
Hàm số	Đồng biến	Nghịch biến	Đồng biến

Bước 4: Tìm cực trị: Hàm số đạt cực đại tại x = 0, y_max = 2. Hàm số đạt cực tiểu tại x = 2, y_min = -2.

Bước 5: Tính đạo hàm cấp hai: y'' = 6x - 6

Bước 6: Tìm điểm uốn: 6x - 6 = 0 => x = 1

Bước 7: Khảo sát tính lồi, lõm:

Khoảng	x < 1	x > 1
y''	-	+
Hàm số	Lồi	Lõm

Điểm uốn của hàm số là (1, 0).

Lưu ý khi giải bài tập

Luôn kiểm tra lại các bước tính toán để tránh sai sót.
Vẽ đồ thị hàm số để kiểm tra lại kết quả khảo sát.
Luyện tập thường xuyên để nắm vững phương pháp giải.

Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài tập 5 trang 40 SGK Toán 12 tập 2 - Cánh diều. Chúc bạn học tập tốt!

Giải bài tập 5 trang 40 SGK Toán 12 tập 2 - Cánh diều

Giải bài tập 5 trang 40 SGK Toán 12 tập 2 - Cánh diều

Giải bài tập 5 trang 40 SGK Toán 12 tập 2 - Cánh diều: Tổng quan và Phương pháp giải

Nội dung chi tiết bài tập 5 trang 40

Lời giải chi tiết bài tập 5 trang 40 (Ví dụ)

Lưu ý khi giải bài tập

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN