Lý thuyết Phương trình mặt phẳng Toán 12 Cánh Diều
Tổng quan nội dung
Lý Thuyết Phương Trình Mặt Phẳng Toán 12 Cánh Diều
Phương trình mặt phẳng là một trong những kiến thức quan trọng trong chương trình Toán 12 Cánh Diều. Nắm vững lý thuyết này giúp học sinh giải quyết các bài toán liên quan đến hình học không gian một cách hiệu quả.
Bài viết này sẽ cung cấp đầy đủ và chi tiết lý thuyết về phương trình mặt phẳng, bao gồm định nghĩa, các dạng phương trình, và cách xác định vectơ pháp tuyến.
1. Vecto pháp tuyến, cặp vecto chỉ phương của mặt phẳng a) Vecto pháp tuyến
1. Vecto pháp tuyến, cặp vecto chỉ phương của mặt phẳng
a) Vecto pháp tuyến
| Vecto \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vecto pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\). |
b) Cặp vecto chỉ phương
| Cho mặt phẳng (P). Hai vecto không cùng phương có giá song song hoặc nằm trong mặt phẳng (P) được gọi là cặp vecto chỉ phương của mặt phẳng (P). |
c) Xác định vecto pháp tuyến của mặt phẳng khi biết cặp vecto chỉ phương
| Nếu hai vecto \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\) là cặp vecto chỉ phương của mặt phẳng (P) thì \(\overrightarrow n = \left[ {\overrightarrow a ;\overrightarrow b } \right] = \left( {\left| {\begin{array}{*{20}{c}}{{a_2}}&{{a_3}}\\{{b_2}}&{{b_3}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{a_3}}&{{a_1}}\\{{b_3}}&{{b_1}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}\\{{b_1}}&{{b_2}}\end{array}} \right|} \right)\). |
2. Phương trình tổng quát của mặt phẳng
| Trong không gian Oxyz, mỗi mặt phẳng đều có phương trình dạng Ax + By + Cz + D = 0, trong đó A, B, C không đồng thời bằng 0, được gọi là phương trình tổng quát của mặt phẳng đó. |
3. Lập phương trình tổng quát của mặt phẳng
Trong không gian Oxyz, nếu mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vecto pháp tuyến \(\overrightarrow n = (A;B;C)\) có phương trình là: \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0 \Leftrightarrow Ax + By + Cz + D = 0\), với \(D = - (A{x_0} + B{y_0} + C{z_0})\). |
Bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vecto chỉ phương:
Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vecto chỉ phương \(\overrightarrow u \), \(\overrightarrow v \) có thể thực hiện theo các bước sau:
- Tìm vecto pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\).
- Lập phương trình tổng quát của mặt phẳng đi qua M và biết vecto pháp tuyến \(\overrightarrow n \).
Bài toán viết phương trình mặt phẳng đi qua ba điểm không thẳng hàng:
Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau:
- Tìm cặp vecto chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \).
- Tìm vecto pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
- Lập phương trình tổng quát của mặt phẳng đi qua A và biết vecto pháp tuyến \(\overrightarrow n \).
4. Điều kiện để hai mặt phẳng vuông góc với nhau
Trong không gian Oxyz, cho hai mặt phẳng: \(\left( \alpha \right):Ax + By + Cz + D = 0,\left( \beta \right):A'x + B'y + C'z + D' = 0,\) với hai vecto pháp tuyến \(\overrightarrow n = (A;B;C)\), \(\overrightarrow {n'} = (A';B';C')\) tương ứng. Khi đó: \(\left( \alpha \right) \bot \left( \beta \right) \Leftrightarrow \overrightarrow n \bot \overrightarrow {n'} \Leftrightarrow AA' + BB' + CC' = 0\). |
5. Điều kiện để hai mặt phẳng song song với nhau
Trong không gian Oxyz, cho hai mặt phẳng: \(\left( \alpha \right):Ax + By + Cz + D = 0,\left( \beta \right):A'x + B'y + C'z + D' = 0,\) với hai vecto pháp tuyến \(\overrightarrow n = (A;B;C)\), \(\overrightarrow {n'} = (A';B';C')\) tương ứng. Khi đó: \(\left( \alpha \right)//\left( \beta \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {n'} = k\overrightarrow n \\D' \ne kD\end{array} \right.\) với k nào đó. |
6. Khoảng cách từ một điểm đến một mặt phẳng
Trong không gian Oxyz, khoảng cách từ điểm \({M_0}({x_0};{y_0};{z_0})\) đến mặt phẳng (P): Ax + By + Cz + D = 0 là: \(d(M,(P)) = \frac{{\left| {A{x_0}{\rm{ }} + {\rm{ }}B{y_0}{\rm{ }} + {\rm{ }}C{z_0}{\rm{ }} + {\rm{ }}D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\) |
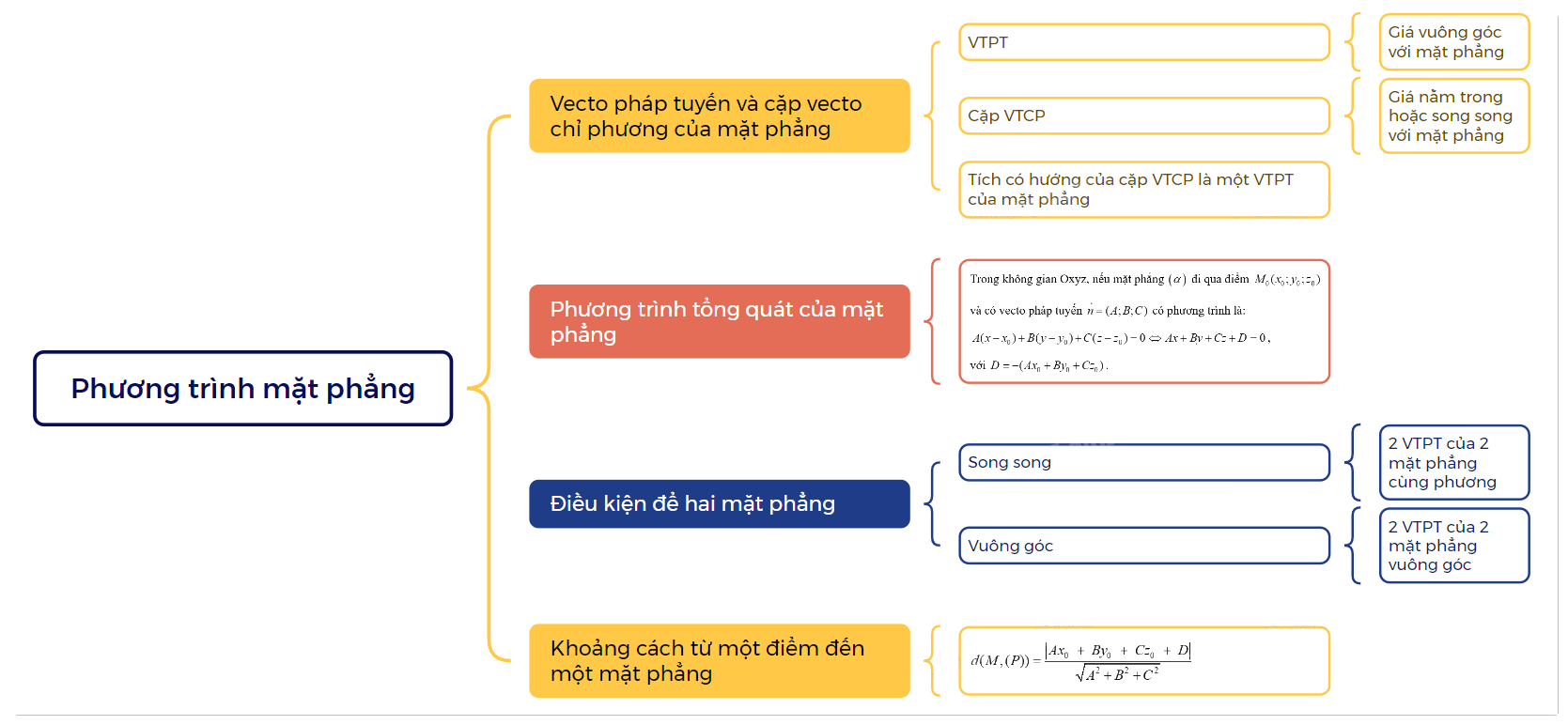
Lý Thuyết Phương Trình Mặt Phẳng Toán 12 Cánh Diều: Tổng Quan Chi Tiết
Trong chương trình Toán 12 Cánh Diều, phương trình mặt phẳng đóng vai trò then chốt trong việc giải quyết các bài toán về hình học không gian. Hiểu rõ lý thuyết và các ứng dụng của nó là điều kiện cần thiết để đạt kết quả cao trong các kỳ thi quan trọng.
1. Định Nghĩa Mặt Phẳng và Vectơ Pháp Tuyến
Mặt phẳng là tập hợp tất cả các điểm trong không gian sao cho vectơ nối điểm đó với một điểm cố định trên mặt phẳng vuông góc với một vectơ cố định gọi là vectơ pháp tuyến của mặt phẳng.
Vectơ pháp tuyếnn của mặt phẳng là vectơ khác không, có hướng vuông góc với mọi vectơ nằm trong mặt phẳng.
2. Các Dạng Phương Trình Mặt Phẳng
Có ba dạng phương trình mặt phẳng thường gặp:
- Phương trình tổng quát của mặt phẳng:ax + by + cz + d = 0, trong đó (a, b, c) là tọa độ của vectơ pháp tuyến n của mặt phẳng.
- Phương trình mặt phẳng đi qua một điểm và có vectơ pháp tuyến:a(x - x0) + b(y - y0) + c(z - z0) = 0, với (x0, y0, z0) là tọa độ của điểm thuộc mặt phẳng và (a, b, c) là tọa độ của vectơ pháp tuyến n.
- Phương trình mặt phẳng đi qua ba điểm không thẳng hàng: Nếu mặt phẳng đi qua ba điểm A(xA, yA, zA), B(xB, yB, zB), C(xC, yC, zC) thì vectơ pháp tuyến n có thể được tính bằng tích có hướng của hai vectơ AB và AC.
3. Xác Định Vectơ Pháp Tuyến của Mặt Phẳng
Có nhiều cách để xác định vectơ pháp tuyến của mặt phẳng:
- Từ phương trình tổng quát: Vectơ pháp tuyến là (a, b, c).
- Từ hai vectơ nằm trong mặt phẳng: Vectơ pháp tuyến là tích có hướng của hai vectơ đó.
- Từ ba điểm thuộc mặt phẳng: Vectơ pháp tuyến là tích có hướng của hai vectơ tạo bởi ba điểm đó.
4. Các Bài Toán Liên Quan và Cách Giải
Một số bài toán thường gặp liên quan đến phương trình mặt phẳng:
- Xác định phương trình mặt phẳng khi biết các yếu tố: Điểm, vectơ pháp tuyến, ba điểm,...
- Tìm giao điểm của mặt phẳng với đường thẳng: Thay phương trình đường thẳng vào phương trình mặt phẳng để tìm tọa độ giao điểm.
- Xác định góc giữa hai mặt phẳng: Sử dụng công thức tính góc giữa hai vectơ pháp tuyến.
- Tìm hình chiếu của một điểm lên mặt phẳng: Sử dụng công thức hình chiếu của vectơ.
5. Ví Dụ Minh Họa
Ví dụ 1: Viết phương trình mặt phẳng đi qua điểm A(1, 2, 3) và có vectơ pháp tuyến n = (2, -1, 1).
Giải: Sử dụng phương trình mặt phẳng đi qua một điểm và có vectơ pháp tuyến: 2(x - 1) - (y - 2) + (z - 3) = 0 => 2x - y + z - 3 = 0.
6. Luyện Tập và Củng Cố Kiến Thức
Để nắm vững lý thuyết phương trình mặt phẳng, bạn nên thực hành giải nhiều bài tập khác nhau. tusach.vn cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết phương trình mặt phẳng Toán 12 Cánh Diều. Chúc bạn học tập tốt!