Giải bài tập 4 trang 43 SGK Toán 12 tập 1 - Cánh diều
Tổng quan nội dung
Giải bài tập 4 trang 43 SGK Toán 12 tập 1 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 4 trang 43 SGK Toán 12 tập 1 - Cánh Diều. Bài tập này thuộc chương trình học Toán 12, tập trung vào việc rèn luyện kỹ năng và kiến thức đã học.
Tusach.vn cung cấp lời giải chính xác, dễ hiểu, giúp các em tự tin hơn trong quá trình học tập và ôn thi.
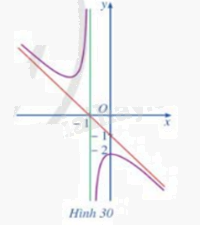
Đường cong ở hình 30 là đồ thị của hàm số:
Đề bài
Đường cong ở hình 30 là đồ thị của hàm số:
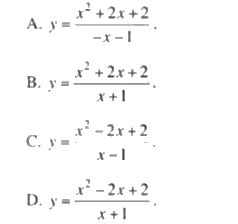
Phương pháp giải - Xem chi tiết
Xét tiệm cận xiên của đồ thị
Xét các hàm số
Lời giải chi tiết
Vì đồ thị hàm số đi qua (0:2)
=> Loại B,D
Vì hàm số có tcd là x=-1
=>\(\mathop {\lim }\limits_{\;x \to - 1} f\left( x \right) = \infty \)
Xét a, \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 2}}{{ - x - 1}} = \mathop {\lim }\limits_{ - x - 1} ( - x - 1 - \frac{1}{{x + 1}}) = - \infty \)
=> Chọn A
Giải bài tập 4 trang 43 SGK Toán 12 tập 1 - Cánh Diều: Hướng dẫn chi tiết và dễ hiểu
Bài tập 4 trang 43 SGK Toán 12 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết và dễ hiểu để giúp các em học sinh nắm vững kiến thức và tự tin giải bài tập này.
Nội dung bài tập 4 trang 43 SGK Toán 12 tập 1 - Cánh Diều
Bài tập yêu cầu tính giới hạn của hàm số tại một điểm cho trước. Để giải bài tập này, các em cần nắm vững các kiến thức sau:
- Khái niệm về giới hạn của hàm số.
- Các định lý về giới hạn.
- Các phương pháp tính giới hạn (ví dụ: phương pháp chia, phương pháp nhân liên hợp).
Lời giải chi tiết bài tập 4 trang 43 SGK Toán 12 tập 1 - Cánh Diều
Để giải bài tập này, chúng ta sẽ sử dụng phương pháp chia tử và mẫu cho x. Cụ thể:
- Chia cả tử và mẫu cho x.
- Sử dụng các định lý về giới hạn để tính giới hạn của từng thành phần.
- Kết hợp các kết quả để tính giới hạn của toàn bộ hàm số.
Ví dụ, nếu bài tập yêu cầu tính lim (x→0) (x^2 + 2x) / x, chúng ta sẽ thực hiện như sau:
- Chia cả tử và mẫu cho x: lim (x→0) (x + 2) / 1
- Thay x = 0 vào biểu thức: 0 + 2 = 2
- Vậy, lim (x→0) (x^2 + 2x) / x = 2
Các bài tập tương tự
Để rèn luyện kỹ năng giải bài tập về giới hạn, các em có thể tham khảo các bài tập tương tự sau:
- Tính lim (x→1) (x^2 - 1) / (x - 1)
- Tính lim (x→2) (x^3 - 8) / (x - 2)
- Tính lim (x→∞) (2x^2 + 3x + 1) / (x^2 + 1)
Lưu ý khi giải bài tập về giới hạn
Khi giải bài tập về giới hạn, các em cần lưu ý những điều sau:
- Nắm vững các định lý về giới hạn.
- Lựa chọn phương pháp tính giới hạn phù hợp.
- Kiểm tra lại kết quả sau khi tính toán.
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là một website cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm:
- Giải bài tập SGK Toán 12 tập 1 và tập 2.
- Giải bài tập trắc nghiệm Toán 12.
- Đề thi thử Toán 12.
- Các bài viết hướng dẫn giải bài tập Toán 12.
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong quá trình học tập và ôn thi Toán 12. Chúc các em học tốt!
| Chương | Bài | Nội dung |
|---|---|---|
| 1 | 1 | Giới hạn của hàm số |
| 1 | 2 | Giới hạn một bên |
| 1 | 3 | Giới hạn tại vô cùng |