Giải mục 1 trang 81, 82 SGK Toán 12 tập 2 - Cánh diều
Tổng quan nội dung
Giải mục 1 trang 81, 82 SGK Toán 12 tập 2 - Cánh diều
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 81, 82 sách giáo khoa Toán 12 tập 2 chương trình Cánh diều. Bài giải này được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và logic.
Chúng tôi hiểu rằng việc tự học Toán 12 có thể gặp nhiều khó khăn. Do đó, tusach.vn luôn cố gắng cung cấp những tài liệu học tập chất lượng nhất, giúp các em học sinh học tập hiệu quả hơn.
Hình 38 mô tả một mặt cầu trong không gian. Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu được lập như thế nào?
LT1
Trả lời câu hỏi Luyện tập 1 trang 82 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; 3) và mặt cầu tâm I đi qua điểm A(0; 4; 5). Tính bán kính R của mặt cầu đó.
Phương pháp giải:
Sử dụng kiến thức về vị trí của điểm so với mặt cầu để tìm bán kính của mặt cầu: Cho mặt cầu tâm I, bán kính R và điểm M bất kì trong không gian. Điểm M thuộc mặt cầu tâm I, bán kính R khi và chỉ khi \(IM = R\).
Lời giải chi tiết:
Vì mặt cầu tâm I đi qua điểm A nên IA là bán kính của mặt cầu.
Bán kính của mặt cầu là: \(R = IA = \sqrt {{{\left( {0 - 1} \right)}^2} + {{\left( {4 - 2} \right)}^2} + {{\left( {5 - 3} \right)}^2}} = 3\).
KĐ
Trả lời câu hỏi khởi động trang 81 SGK Toán 12 Cánh diều
Hình 38 mô tả một mặt cầu trong không gian.
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu được lập như thế nào?

Phương pháp giải:
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu tâm I(a; b; c) bán kính R là: \(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R\).
Lời giải chi tiết:
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu tâm I(a; b; c) bán kính R là: \(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R\).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 81 SGK Toán 12 Cánh diều
Nếu quay đường tròn tâm I bán kính R quanh đường kính AB một vòng (Hình 39) thì hình tạo thành được gọi là mặt cầu. Những điểm thuộc mặt cầu đó cách I một khoảng bằng bao nhiêu?
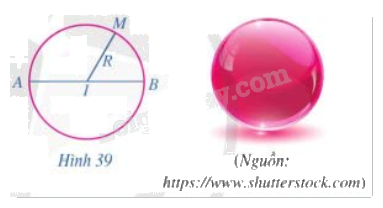
Phương pháp giải:
Khi quay đường tròn tâm I bán kính R quanh đường kính AB một vòng thì điểm thuộc mặt cầu đó cách I một khoảng bằng R.
Lời giải chi tiết:
Khi quay đường tròn tâm I bán kính R quanh đường kính AB một vòng thì điểm thuộc mặt cầu đó cách I một khoảng bằng R.
- KĐ
- HĐ1
- LT1
Trả lời câu hỏi khởi động trang 81 SGK Toán 12 Cánh diều
Hình 38 mô tả một mặt cầu trong không gian.
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu được lập như thế nào?

Phương pháp giải:
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu tâm I(a; b; c) bán kính R là: \(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R\).
Lời giải chi tiết:
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu tâm I(a; b; c) bán kính R là: \(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R\).
Trả lời câu hỏi Hoạt động 1 trang 81 SGK Toán 12 Cánh diều
Nếu quay đường tròn tâm I bán kính R quanh đường kính AB một vòng (Hình 39) thì hình tạo thành được gọi là mặt cầu. Những điểm thuộc mặt cầu đó cách I một khoảng bằng bao nhiêu?
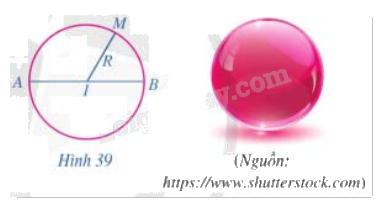
Phương pháp giải:
Khi quay đường tròn tâm I bán kính R quanh đường kính AB một vòng thì điểm thuộc mặt cầu đó cách I một khoảng bằng R.
Lời giải chi tiết:
Khi quay đường tròn tâm I bán kính R quanh đường kính AB một vòng thì điểm thuộc mặt cầu đó cách I một khoảng bằng R.
Trả lời câu hỏi Luyện tập 1 trang 82 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; 3) và mặt cầu tâm I đi qua điểm A(0; 4; 5). Tính bán kính R của mặt cầu đó.
Phương pháp giải:
Sử dụng kiến thức về vị trí của điểm so với mặt cầu để tìm bán kính của mặt cầu: Cho mặt cầu tâm I, bán kính R và điểm M bất kì trong không gian. Điểm M thuộc mặt cầu tâm I, bán kính R khi và chỉ khi \(IM = R\).
Lời giải chi tiết:
Vì mặt cầu tâm I đi qua điểm A nên IA là bán kính của mặt cầu.
Bán kính của mặt cầu là: \(R = IA = \sqrt {{{\left( {0 - 1} \right)}^2} + {{\left( {4 - 2} \right)}^2} + {{\left( {5 - 3} \right)}^2}} = 3\).
Giải mục 1 trang 81, 82 SGK Toán 12 tập 2 - Cánh diều: Tổng quan và Hướng dẫn chi tiết
Mục 1 trang 81, 82 SGK Toán 12 tập 2 - Cánh diều thuộc chương trình học về Đường thẳng và mặt phẳng trong không gian. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học nâng cao hơn. Việc nắm vững các khái niệm và phương pháp giải bài tập trong mục này là vô cùng cần thiết để đạt kết quả tốt trong các kỳ thi.
Nội dung chính của Mục 1 trang 81, 82
Mục 1 tập trung vào việc ôn tập và hệ thống hóa kiến thức về:
- Vecto trong không gian: Các khái niệm cơ bản về vecto, các phép toán trên vecto (cộng, trừ, nhân với một số).
- Quan hệ song song và vuông góc trong không gian: Điều kiện để hai đường thẳng song song, vuông góc, cắt nhau. Điều kiện để đường thẳng vuông góc với mặt phẳng.
- Góc giữa hai đường thẳng, giữa đường thẳng và mặt phẳng: Cách tính góc giữa hai đường thẳng, giữa đường thẳng và mặt phẳng.
- Khoảng cách trong không gian: Cách tính khoảng cách từ một điểm đến một mặt phẳng, từ một điểm đến một đường thẳng.
Hướng dẫn giải chi tiết các bài tập trong Mục 1
Dưới đây là hướng dẫn giải chi tiết các bài tập trong Mục 1 trang 81, 82 SGK Toán 12 tập 2 - Cánh diều:
Bài 1: (Trang 81)
Bài 1 yêu cầu học sinh vận dụng kiến thức về vecto để chứng minh một số đẳng thức vecto. Để giải bài này, cần nắm vững các quy tắc cộng, trừ vecto và quy tắc nhân với một số.
Ví dụ: Cho hai điểm A và B. Chứng minh rằng AB = BA.
Lời giải: Theo định nghĩa vecto, AB là vecto có điểm đầu là A và điểm cuối là B. Tương tự, BA là vecto có điểm đầu là B và điểm cuối là A. Do đó, AB và BA là hai vecto ngược chiều và có cùng độ dài, suy ra AB = BA.
Bài 2: (Trang 82)
Bài 2 yêu cầu học sinh vận dụng kiến thức về quan hệ song song và vuông góc trong không gian để chứng minh một số mệnh đề. Để giải bài này, cần nắm vững các điều kiện để hai đường thẳng song song, vuông góc, cắt nhau.
Ví dụ: Cho hai đường thẳng a và b. Chứng minh rằng nếu a song song với b thì mọi đường thẳng nằm trong mặt phẳng chứa a và song song với b đều song song với a.
Lời giải: Gọi (P) là mặt phẳng chứa a và song song với b. Gọi c là một đường thẳng nằm trong (P) và song song với b. Theo tính chất của đường thẳng song song, c song song với a. Vậy mọi đường thẳng nằm trong mặt phẳng chứa a và song song với b đều song song với a.
Mẹo học tập hiệu quả
- Nắm vững định nghĩa và tính chất: Đây là nền tảng để giải quyết mọi bài tập.
- Vẽ hình minh họa: Việc vẽ hình minh họa giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Luyện tập thường xuyên: Luyện tập thường xuyên giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải bài tập.
- Tham khảo các nguồn tài liệu khác: Ngoài SGK, bạn có thể tham khảo thêm các tài liệu tham khảo, bài giảng trên mạng để hiểu sâu hơn về kiến thức.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục kiến thức Toán 12. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết, và các mẹo học tập hiệu quả. Hãy truy cập tusach.vn để được hỗ trợ tốt nhất!
Chúc các bạn học tập tốt!