Giải mục 1 trang 97, 98, 99, 100 SGK Toán 12 tập 2 - Cánh diều
Tổng quan nội dung
Giải mục 1 trang 97, 98, 99, 100 SGK Toán 12 tập 2 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 97, 98, 99, 100 SGK Toán 12 tập 2 chương trình Cánh Diều. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập phức tạp. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của tusach.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp các em nắm vững kiến thức và tự tin làm bài.
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra. Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là bao nhiêu?
LT1
Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cánh diều
Hãy giải bài toán mở đầu bằng cách lập bảng thống kê như trong Ví dụ 2, biết rằng cả hai nhà máy sản xuất được 10 000 linh kiện.
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra.
Phương pháp giải:
Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
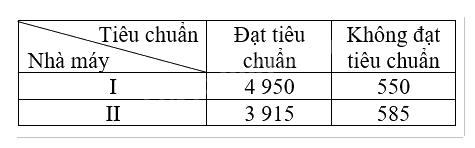
Số linh kiện do nhà máy I sản xuất là: \(10\;000.55\% = 5\;500\) (linh kiện).
Số linh kiện do nhà máy II sản xuất là: \(10\;000.45\% = 4\;500\) (linh kiện).
Số linh do nhà máy I sản xuất đạt tiêu chuẩn là:
\(5\;500.90\% = 4\;950\) (linh kiện).
Số linh do nhà máy I sản xuất không đạt tiêu chuẩn là: \(5\;500 - 4\;950 = 550\) (linh kiện).
Số linh do nhà máy II sản xuất đạt tiêu chuẩn là: \(4\;500.87\% = 3\;915\) (linh kiện).
Số linh do nhà máy II sản xuất không đạt tiêu chuẩn là: \(4\;500 - 3\;915 = 585\) (linh kiện).
Ta có bảng thống kê như sau:
Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\).
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 97 SGK Toán 12 Cánh diều
Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
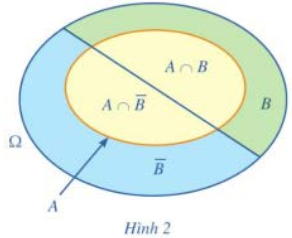
a) Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, \(A \cap B,A \cap \overline B \) (Hình 2).
b) So sánh n(A) và \(n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)\). Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right)\).
c) So sánh \(P\left( {A \cap B} \right)\) và \(P\left( B \right).P\left( {A|B} \right)\);
\(P\left( {A \cap \overline B } \right)\) và \(P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Phương pháp giải:
+ Sử dụng kiến thức về định nghĩa xác suất có điều kiện để tính: Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B, kí hiệu là P(A|B). Nếu \(P\left( B \right) > 0\) thì \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\).
+ Sử dụng kiến thức về công thức tính xác suất của hai biến cố xung khắc: Nếu A và B là hai biến cố xung khắc thì \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
Lời giải chi tiết:
a) \(A = \left\{ {3;{\rm{ }}6;{\rm{ }}9;{\rm{ }}12;{\rm{ }}15;{\rm{ }}18;{\rm{ }}21;{\rm{ }}24} \right\},B = \left\{ {4;{\rm{ }}8;{\rm{ }}12;{\rm{ }}16;{\rm{ }}20;{\rm{ }}24} \right\}\), \(\Omega = \left\{ {1;2;3;...;24} \right\}\)\(A \cap B = \left\{ {12;24} \right\},A \cap \overline B = \left\{ {3;6;9;15;18;21} \right\}\).
b) Ta có: \(n\left( A \right) = 8,n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right) = 2 + 6 = 8\) nên \(n\left( A \right) = n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)\).
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)}}{{n\left( \Omega \right)}} = \frac{{n\left( {A \cap B} \right)}}{{n\left( \Omega \right)}} + \frac{{n\left( {A \cap \overline B } \right)}}{{n\left( \Omega \right)}} = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right)\)
c) Ta có: \(P\left( B \right).P\left( {A|B} \right) = P\left( B \right).\frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = P\left( {A \cap B} \right)\);
\(P\left( {\overline B } \right).P\left( {A|\overline B } \right) = P\left( {\overline B } \right).\frac{{P\left( {A \cap \overline B } \right)}}{{P\left( {\overline B } \right)}} = P\left( {A \cap \overline B } \right)\).
Vì \(A \cap B,A \cap \overline B \) là hai biến cố xung khắc nên \(\left( {A \cap B} \right) \cup \left( {A \cap \overline B } \right) = A\), theo công thức xác suất ta có: \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
LT2
Trả lời câu hỏi Luyện tập 2 trang 100 SGK Toán 12 Cánh diều
Hãy giải bài toán mở đầu bằng phương pháp sử dụng sơ đồ hình cây như trong Ví dụ 3.
Phương pháp giải:
+ Sử dụng kiến thức sơ đồ hình cây để tính.
+ Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {B|A} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
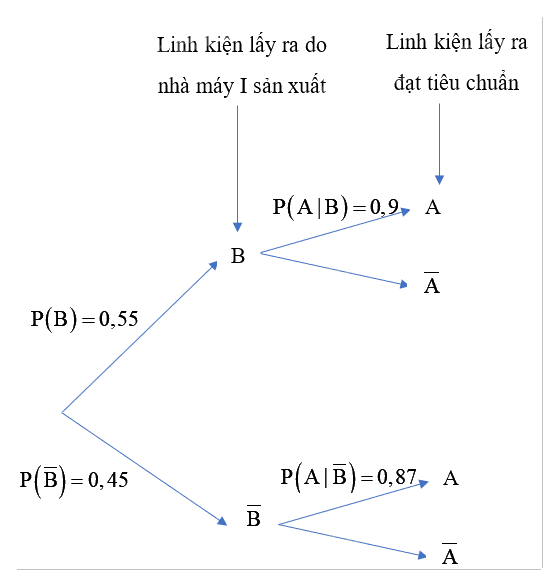
Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\)
Sơ đồ hình cây biểu thị tình huống đã cho:
 p
p
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {B|A} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
MĐ
Trả lời câu hỏi Bài toán mở đầu trang 97 SGK Toán 12 Cánh diều
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra. Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là bao nhiêu?

Phương pháp giải:
Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\)
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
- MĐ
- HĐ1
- LT1
- LT2
Trả lời câu hỏi Bài toán mở đầu trang 97 SGK Toán 12 Cánh diều
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra. Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là bao nhiêu?

Phương pháp giải:
Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\)
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
Trả lời câu hỏi Hoạt động 1 trang 97 SGK Toán 12 Cánh diều
Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
a) Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, \(A \cap B,A \cap \overline B \) (Hình 2).

b) So sánh n(A) và \(n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)\). Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right)\).
c) So sánh \(P\left( {A \cap B} \right)\) và \(P\left( B \right).P\left( {A|B} \right)\);
\(P\left( {A \cap \overline B } \right)\) và \(P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Phương pháp giải:
+ Sử dụng kiến thức về định nghĩa xác suất có điều kiện để tính: Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B, kí hiệu là P(A|B). Nếu \(P\left( B \right) > 0\) thì \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\).
+ Sử dụng kiến thức về công thức tính xác suất của hai biến cố xung khắc: Nếu A và B là hai biến cố xung khắc thì \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
Lời giải chi tiết:
a) \(A = \left\{ {3;{\rm{ }}6;{\rm{ }}9;{\rm{ }}12;{\rm{ }}15;{\rm{ }}18;{\rm{ }}21;{\rm{ }}24} \right\},B = \left\{ {4;{\rm{ }}8;{\rm{ }}12;{\rm{ }}16;{\rm{ }}20;{\rm{ }}24} \right\}\), \(\Omega = \left\{ {1;2;3;...;24} \right\}\)\(A \cap B = \left\{ {12;24} \right\},A \cap \overline B = \left\{ {3;6;9;15;18;21} \right\}\).
b) Ta có: \(n\left( A \right) = 8,n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right) = 2 + 6 = 8\) nên \(n\left( A \right) = n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)\).
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)}}{{n\left( \Omega \right)}} = \frac{{n\left( {A \cap B} \right)}}{{n\left( \Omega \right)}} + \frac{{n\left( {A \cap \overline B } \right)}}{{n\left( \Omega \right)}} = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right)\)
c) Ta có: \(P\left( B \right).P\left( {A|B} \right) = P\left( B \right).\frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = P\left( {A \cap B} \right)\);
\(P\left( {\overline B } \right).P\left( {A|\overline B } \right) = P\left( {\overline B } \right).\frac{{P\left( {A \cap \overline B } \right)}}{{P\left( {\overline B } \right)}} = P\left( {A \cap \overline B } \right)\).
Vì \(A \cap B,A \cap \overline B \) là hai biến cố xung khắc nên \(\left( {A \cap B} \right) \cup \left( {A \cap \overline B } \right) = A\), theo công thức xác suất ta có: \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cánh diều
Hãy giải bài toán mở đầu bằng cách lập bảng thống kê như trong Ví dụ 2, biết rằng cả hai nhà máy sản xuất được 10 000 linh kiện.
Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra.
Phương pháp giải:
Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
Số linh kiện do nhà máy I sản xuất là: \(10\;000.55\% = 5\;500\) (linh kiện).
Số linh kiện do nhà máy II sản xuất là: \(10\;000.45\% = 4\;500\) (linh kiện).
Số linh do nhà máy I sản xuất đạt tiêu chuẩn là:
\(5\;500.90\% = 4\;950\) (linh kiện).
Số linh do nhà máy I sản xuất không đạt tiêu chuẩn là: \(5\;500 - 4\;950 = 550\) (linh kiện).
Số linh do nhà máy II sản xuất đạt tiêu chuẩn là: \(4\;500.87\% = 3\;915\) (linh kiện).
Số linh do nhà máy II sản xuất không đạt tiêu chuẩn là: \(4\;500 - 3\;915 = 585\) (linh kiện).
Ta có bảng thống kê như sau:

Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\).
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
Trả lời câu hỏi Luyện tập 2 trang 100 SGK Toán 12 Cánh diều
Hãy giải bài toán mở đầu bằng phương pháp sử dụng sơ đồ hình cây như trong Ví dụ 3.
Phương pháp giải:
+ Sử dụng kiến thức sơ đồ hình cây để tính.
+ Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {B|A} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết:
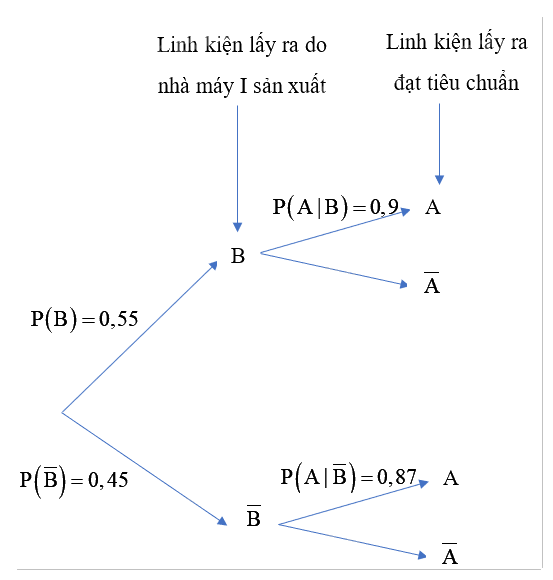
Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\)
Sơ đồ hình cây biểu thị tình huống đã cho:
 p
p
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {B|A} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).
Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.
Giải mục 1 trang 97, 98, 99, 100 SGK Toán 12 tập 2 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Mục 1 của chương trình Toán 12 tập 2 Cánh Diều tập trung vào các kiến thức về Đường thẳng và mặt phẳng trong không gian. Đây là một phần quan trọng, nền tảng cho việc học các kiến thức hình học không gian ở các lớp trên. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập trong mục này là vô cùng cần thiết để đạt kết quả tốt trong các kỳ thi.
Nội dung chính của Mục 1
- Đường thẳng trong không gian: Định nghĩa, các dạng biểu diễn, vị trí tương đối của hai đường thẳng.
- Mặt phẳng trong không gian: Định nghĩa, các dạng biểu diễn, vị trí tương đối của hai mặt phẳng, đường thẳng và mặt phẳng.
- Góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng: Cách tính góc, các ứng dụng.
- Khoảng cách: Khoảng cách từ một điểm đến một đường thẳng, một mặt phẳng; khoảng cách giữa hai đường thẳng chéo nhau.
Giải chi tiết các bài tập trang 97, 98, 99, 100
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1, trang 97, 98, 99, 100 SGK Toán 12 tập 2 Cánh Diều:
Bài 1 (Trang 97)
Đề bài: (Đề bài cụ thể của bài 1)
Lời giải: (Lời giải chi tiết, bao gồm các bước giải, công thức sử dụng và kết luận)
Bài 2 (Trang 98)
Đề bài: (Đề bài cụ thể của bài 2)
Lời giải: (Lời giải chi tiết, bao gồm các bước giải, công thức sử dụng và kết luận)
Bài 3 (Trang 99)
Đề bài: (Đề bài cụ thể của bài 3)
Lời giải: (Lời giải chi tiết, bao gồm các bước giải, công thức sử dụng và kết luận)
Bài 4 (Trang 100)
Đề bài: (Đề bài cụ thể của bài 4)
Lời giải: (Lời giải chi tiết, bao gồm các bước giải, công thức sử dụng và kết luận)
Mẹo giải bài tập hiệu quả
- Nắm vững định nghĩa và tính chất: Đây là nền tảng để giải quyết mọi bài toán.
- Vẽ hình: Hình vẽ giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Sử dụng công thức: Áp dụng đúng công thức là yếu tố quan trọng để có kết quả chính xác.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn cam kết cung cấp cho bạn những lời giải chính xác, dễ hiểu và đầy đủ nhất. Chúng tôi luôn cập nhật kiến thức mới nhất và phương pháp giải bài tập hiệu quả nhất để giúp bạn đạt kết quả tốt nhất trong học tập. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chương | Bài | Trang |
|---|---|---|
| Chương 6 | Mục 1 | 97-100 |