Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Cánh diều
Tổng quan nội dung
Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 chương trình Cánh Diều. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và lời giải dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả cao trong môn Toán.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bằng đạo hàm
LT3
Trả lời câu hỏi Luyện tập 3 trang 18 SGK Toán 12 Cánh diều
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \sin 2x - 2x\) trên đoạn \(\left[ {\frac{\pi }{2};\frac{{3\pi }}{2}} \right]\).
Phương pháp giải:
B1: Tìm các điểm \({x_1},{x_2},...,{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
B2: Tính \(f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),f\left( a \right),f\left( b \right)\)
B3: So sánh các giá trị tìm được ở bước 2 và kết luận
Lời giải chi tiết:
Ta có: \(f'\left( x \right) = 2\cos 2x - 2\).
Xét \(f'\left( x \right) = 0 \Leftrightarrow x = \pi \).
Ta có \(f\left( {\frac{\pi }{2}} \right) = - \pi ,f\left( \pi \right) = - 2\pi ,f\left( {\frac{{3\pi }}{2}} \right) = - 3\pi \)
Vậy hàm số \(f\left( x \right) = \sin 2x - 2x\) có giá trị nhỏ nhất bằng \( - 3\pi \) khi \(x = \frac{{3\pi }}{2}\) và có giá trị lớn nhất bằng \( - \pi \) khi \(x = \frac{\pi }{2}\) .
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 17SGK Toán 12 Cánh diều
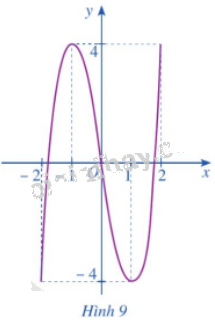
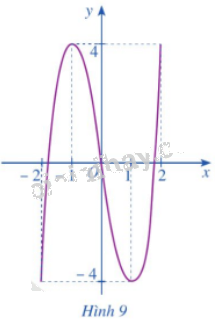
Cho hàm số \(y = f\left( x \right) = 2{x^3} - 6x,x \in \left[ { - 2;2} \right]\) có đồ thị là đường cong ở Hình 9.
a) Dựa vào đồ thị ở Hình 9, hãy cho biết các giá trị \(M = \mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right);m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right)\) bằng bao nhiêu.
b) Giải phương trình \(f'\left( x \right) = 0\) với \(x \in \left( { - 2;2} \right)\)
c) Tính các giá trị của hàm số \(f\left( x \right)\) tại hai đầu mút \( - 2;2\) và tại các điểm \(x \in \left( { - 2;2} \right)\) mà ở đó \(f'\left( x \right) = 0\)
d) So sánh M (hoặc m) với số lớn nhất (hoặc số bé nhất) trong các giá trị tính được ở câu c
Lời giải chi tiết:
a) Ta có: \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = 4\\\mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 4\end{array} \right.\).
b) Ta có: \(f'\left( x \right) = 6{x^2} - 6\).
Xét \(f'\left( x \right) = 0 \Leftrightarrow x = \pm 1\).
c) Ta có:\(\left\{ \begin{array}{l}f\left( 2 \right) = f\left( { - 1} \right) = 4\\f\left( { - 2} \right) = f\left( 1 \right) = - 4\end{array} \right.\).
d) Nhận xét: \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = f\left( 2 \right) = f\left( { - 1} \right)\\\mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = f\left( { - 2} \right) = f\left( 1 \right)\end{array} \right.\).
LT2
Trả lời câu hỏi Luyện tập 2 trang 16 SGK Toán 12 Cánh diều
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số \(y = \frac{{2x - 5}}{{x - 1}}\) trên nửa khoảng \((1;3]\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
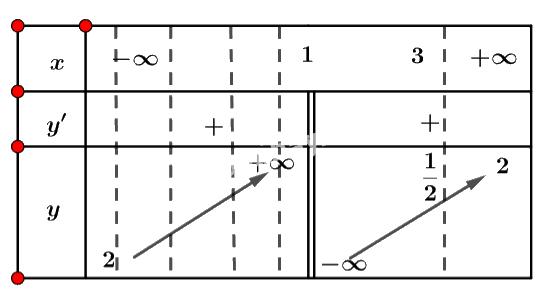
Ta có: \(y' = \frac{3}{{{{\left( {x - 1} \right)}^2}}}\).
Nhận xét \(y' > 0{\rm{ }}\forall x \in D\).
Ta có bảng biến thiên:
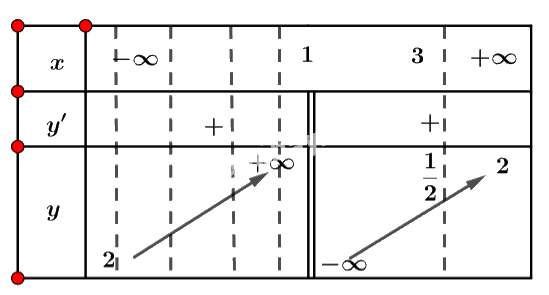
Vậy hàm số có giá trị lớn nhất bằng \(\frac{1}{2}\) khi \(x = 3\) và không có giá trị nhỏ nhất.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 16 SGK Toán 12 Cánh diều
Cho hàm số \(f\left( x \right) = x + \frac{1}{{x - 1}}\) với \(x > 1\).
a) Tính \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\).
b) Lập bảng biến thiên của hàm số \(f\left( x \right)\) trên khoảng \(\left( {1; + \infty } \right)\).
c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số \(f\left( x \right)\) trên khoảng \(\left( {1; + \infty } \right)\).
Phương pháp giải:
a) Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \\\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \end{array} \right.\)
b) Bảng biến thiên của hàm số trên khoảng \(\left( {1; + \infty } \right)\) là:

c) Hàm số có giá trị nhỏ nhất bằng 3 khi \(x = 2\) và không có giá trị lớn nhất.
Lời giải chi tiết:
a) Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \\\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \end{array} \right.\)
b) Bảng biến thiên của hàm số trên khoảng \(\left( {1; + \infty } \right)\) là:
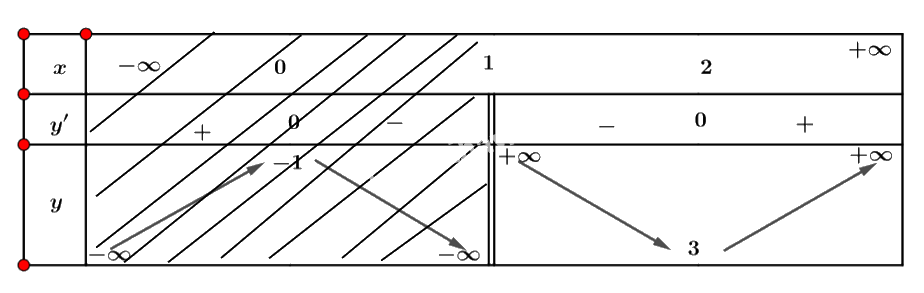
c) Hàm số có giá trị nhỏ nhất bằng 3 khi \(x = 2\) và không có giá trị lớn nhất.
- HĐ2
- LT2
- HĐ3
- LT3
Trả lời câu hỏi Hoạt động 2 trang 16 SGK Toán 12 Cánh diều
Cho hàm số \(f\left( x \right) = x + \frac{1}{{x - 1}}\) với \(x > 1\).
a) Tính \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\).
b) Lập bảng biến thiên của hàm số \(f\left( x \right)\) trên khoảng \(\left( {1; + \infty } \right)\).
c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số \(f\left( x \right)\) trên khoảng \(\left( {1; + \infty } \right)\).
Phương pháp giải:
a) Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \\\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \end{array} \right.\)
b) Bảng biến thiên của hàm số trên khoảng \(\left( {1; + \infty } \right)\) là:

c) Hàm số có giá trị nhỏ nhất bằng 3 khi \(x = 2\) và không có giá trị lớn nhất.
Lời giải chi tiết:
a) Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \\\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \end{array} \right.\)
b) Bảng biến thiên của hàm số trên khoảng \(\left( {1; + \infty } \right)\) là:
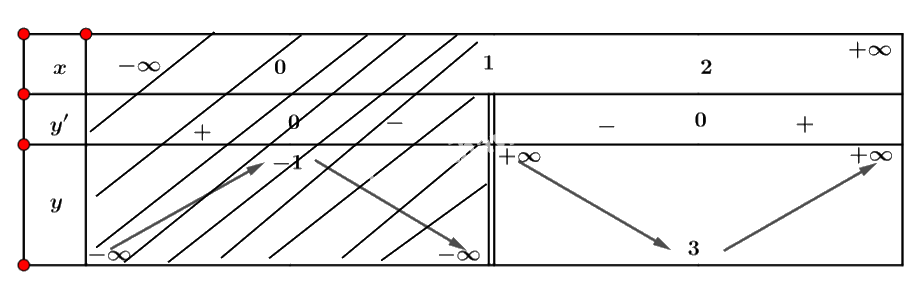
c) Hàm số có giá trị nhỏ nhất bằng 3 khi \(x = 2\) và không có giá trị lớn nhất.
Trả lời câu hỏi Luyện tập 2 trang 16 SGK Toán 12 Cánh diều
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số \(y = \frac{{2x - 5}}{{x - 1}}\) trên nửa khoảng \((1;3]\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Ta có: \(y' = \frac{3}{{{{\left( {x - 1} \right)}^2}}}\).
Nhận xét \(y' > 0{\rm{ }}\forall x \in D\).
Ta có bảng biến thiên:
Vậy hàm số có giá trị lớn nhất bằng \(\frac{1}{2}\) khi \(x = 3\) và không có giá trị nhỏ nhất.
Trả lời câu hỏi Hoạt động 3 trang 17SGK Toán 12 Cánh diều
Cho hàm số \(y = f\left( x \right) = 2{x^3} - 6x,x \in \left[ { - 2;2} \right]\) có đồ thị là đường cong ở Hình 9.
a) Dựa vào đồ thị ở Hình 9, hãy cho biết các giá trị \(M = \mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right);m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right)\) bằng bao nhiêu.
b) Giải phương trình \(f'\left( x \right) = 0\) với \(x \in \left( { - 2;2} \right)\)
c) Tính các giá trị của hàm số \(f\left( x \right)\) tại hai đầu mút \( - 2;2\) và tại các điểm \(x \in \left( { - 2;2} \right)\) mà ở đó \(f'\left( x \right) = 0\)
d) So sánh M (hoặc m) với số lớn nhất (hoặc số bé nhất) trong các giá trị tính được ở câu c
Lời giải chi tiết:
a) Ta có: \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = 4\\\mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 4\end{array} \right.\).
b) Ta có: \(f'\left( x \right) = 6{x^2} - 6\).
Xét \(f'\left( x \right) = 0 \Leftrightarrow x = \pm 1\).
c) Ta có:\(\left\{ \begin{array}{l}f\left( 2 \right) = f\left( { - 1} \right) = 4\\f\left( { - 2} \right) = f\left( 1 \right) = - 4\end{array} \right.\).
d) Nhận xét: \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = f\left( 2 \right) = f\left( { - 1} \right)\\\mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = f\left( { - 2} \right) = f\left( 1 \right)\end{array} \right.\).
Trả lời câu hỏi Luyện tập 3 trang 18 SGK Toán 12 Cánh diều
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \sin 2x - 2x\) trên đoạn \(\left[ {\frac{\pi }{2};\frac{{3\pi }}{2}} \right]\).
Phương pháp giải:
B1: Tìm các điểm \({x_1},{x_2},...,{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
B2: Tính \(f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),f\left( a \right),f\left( b \right)\)
B3: So sánh các giá trị tìm được ở bước 2 và kết luận
Lời giải chi tiết:
Ta có: \(f'\left( x \right) = 2\cos 2x - 2\).
Xét \(f'\left( x \right) = 0 \Leftrightarrow x = \pi \).
Ta có \(f\left( {\frac{\pi }{2}} \right) = - \pi ,f\left( \pi \right) = - 2\pi ,f\left( {\frac{{3\pi }}{2}} \right) = - 3\pi \)
Vậy hàm số \(f\left( x \right) = \sin 2x - 2x\) có giá trị nhỏ nhất bằng \( - 3\pi \) khi \(x = \frac{{3\pi }}{2}\) và có giá trị lớn nhất bằng \( - \pi \) khi \(x = \frac{\pi }{2}\) .
Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Mục 2 của SGK Toán 12 tập 1 Cánh Diều tập trung vào việc ôn tập về hàm số bậc hai, bao gồm các kiến thức cơ bản về định nghĩa, tính chất, đồ thị và ứng dụng của hàm số này. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Nội dung chính của Mục 2
- Ôn tập về hàm số bậc hai: Định nghĩa, dạng tổng quát, hệ số a, b, c và ảnh hưởng của chúng đến đồ thị.
- Đồ thị hàm số bậc hai: Xác định đỉnh, trục đối xứng, giao điểm với các trục tọa độ.
- Ứng dụng của hàm số bậc hai: Giải các bài toán thực tế liên quan đến quỹ đạo, diện tích, và các vấn đề tối ưu hóa.
Giải chi tiết các bài tập trang 16, 17, 18
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2, trang 16, 17, 18 SGK Toán 12 tập 1 Cánh Diều:
Bài 1: (Trang 16)
Đề bài: Xác định hệ số a, b, c của hàm số y = 2x2 - 5x + 3.
Lời giải:
- Hệ số a là 2.
- Hệ số b là -5.
- Hệ số c là 3.
Bài 2: (Trang 17)
Đề bài: Vẽ đồ thị hàm số y = x2 - 4x + 3.
Lời giải:
- Xác định đỉnh: xđỉnh = -b/2a = 2. yđỉnh = (2)2 - 4(2) + 3 = -1. Vậy đỉnh là (2, -1).
- Xác định trục đối xứng: x = 2.
- Xác định giao điểm với trục Oy: x = 0 => y = 3. Vậy giao điểm là (0, 3).
- Xác định giao điểm với trục Ox: y = 0 => x2 - 4x + 3 = 0 => x = 1 hoặc x = 3. Vậy giao điểm là (1, 0) và (3, 0).
- Vẽ đồ thị dựa trên các thông tin trên.
Bài 3: (Trang 18)
Đề bài: Tìm giá trị lớn nhất của hàm số y = -x2 + 6x - 5.
Lời giải:
Hàm số có dạng y = ax2 + bx + c với a = -1 < 0, nên hàm số đạt giá trị lớn nhất tại đỉnh.
xđỉnh = -b/2a = -6/(2*(-1)) = 3.
yđỉnh = -(3)2 + 6(3) - 5 = 4.
Vậy giá trị lớn nhất của hàm số là 4.
Lưu ý khi giải bài tập
- Luôn xác định đúng các hệ số a, b, c của hàm số.
- Nắm vững các công thức tính đỉnh, trục đối xứng và giao điểm của đồ thị hàm số.
- Sử dụng các phương pháp giải phương trình bậc hai để tìm nghiệm của hàm số.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Đồng hành cùng bạn học Toán 12
Tusach.vn cung cấp đầy đủ lời giải chi tiết, đáp án chính xác cho tất cả các bài tập trong SGK Toán 12 tập 1 Cánh Diều. Chúng tôi hy vọng rằng với sự hỗ trợ của Tusach.vn, các em sẽ học tập hiệu quả và đạt được kết quả tốt nhất trong môn Toán.
Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!