Giải bài tập 4 trang 13 SGK Toán 12 tập 1 - Cánh diều
Tổng quan nội dung
Giải bài tập 4 trang 13 SGK Toán 12 tập 1 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 4 trang 13 SGK Toán 12 tập 1 - Cánh Diều. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu sắc kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em.
Tìm cực trị của mỗi hàm số sau: a) (y = 2{x^3} + 3{x^2} - 36x - 10) b) (y = -{x^4} - 2{x^2} - 3) c) (y = x + frac{1}{x})
Đề bài
Tìm cực trị của mỗi hàm số sau:
a) \(y = 2{x^3} + 3{x^2} - 36x - 10\)
b) \(y = -{x^4} - 2{x^2} - 3\)
c) \(y = x + \frac{1}{x}\)
Phương pháp giải - Xem chi tiết
B1: Tìm tập xác định của hàm số.
B2: Tính đạo hàm. Tìm các điểm mà tại đó đạo hàm bằng không hoặc không tồn tại.
B3: Lập bảng biến thiên.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết
a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = 6{x^2} + 6x - 36\).
Nhận xét \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 3\end{array} \right.\).
Ta có bảng biến thiên sau:
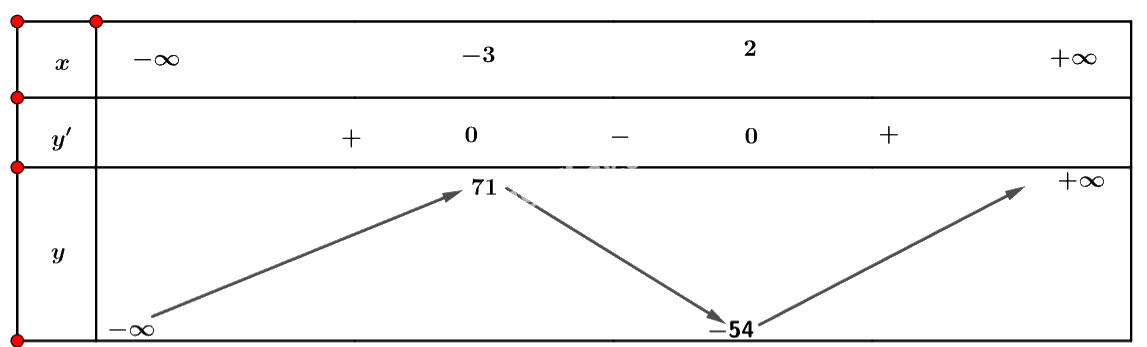
Vậy hàm số đạt cực đại tại điểm \(x = - 3\) và đạt cực tiểu tại \(x = 2\).
b) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = -{4x^3} - 4x\).
Nhận xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên sau:
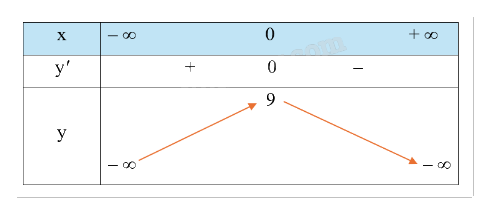
Vậy hàm số đạt cực tiểu tại \(x = 0\).
c) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
Ta có: \(y' = 1 - \frac{1}{{{x^2}}}\).
Nhận xét: \(y' = 0 \Leftrightarrow 1 - \frac{1}{{{x^2}}} = 0 \Leftrightarrow x = \pm 1\).
Ta có bảng biến thiên sau:
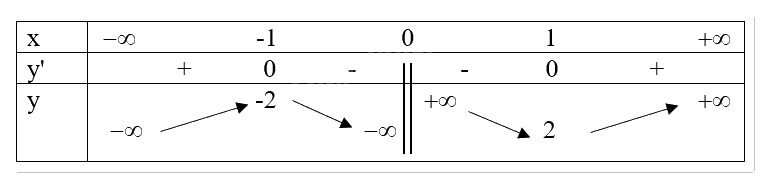
Vậy hàm số đạt cực đại tại x = -1 và đạt cực tiểu tại x = 1.
Giải bài tập 4 trang 13 SGK Toán 12 tập 1 - Cánh Diều: Hướng dẫn chi tiết và dễ hiểu
Bài tập 4 trang 13 SGK Toán 12 tập 1 - Cánh Diều thuộc chương trình học về giới hạn của hàm số. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học toán cao hơn. Việc nắm vững kiến thức và kỹ năng giải bài tập trong chương này sẽ giúp các em tự tin hơn trong các kỳ thi sắp tới.
Nội dung bài tập 4 trang 13 SGK Toán 12 tập 1 - Cánh Diều
Bài tập 4 yêu cầu các em tính giới hạn của hàm số tại một điểm cho trước. Để giải bài tập này, các em cần nắm vững các định nghĩa và tính chất của giới hạn hàm số, cũng như các phương pháp tính giới hạn thường gặp.
Phương pháp giải bài tập 4 trang 13 SGK Toán 12 tập 1 - Cánh Diều
Có nhiều phương pháp để giải bài tập tính giới hạn hàm số, tùy thuộc vào dạng của hàm số. Dưới đây là một số phương pháp thường được sử dụng:
- Phương pháp trực tiếp: Thay trực tiếp giá trị của x vào hàm số để tính giới hạn. Phương pháp này chỉ áp dụng được khi hàm số liên tục tại điểm đó.
- Phương pháp phân tích thành nhân tử: Phân tích tử số và mẫu số thành nhân tử để rút gọn biểu thức, sau đó thay giá trị của x vào để tính giới hạn.
- Phương pháp nhân liên hợp: Nhân cả tử số và mẫu số với liên hợp của biểu thức để khử dạng vô định.
- Phương pháp sử dụng định lý giới hạn: Áp dụng các định lý giới hạn để tính giới hạn của hàm số.
Lời giải chi tiết bài tập 4 trang 13 SGK Toán 12 tập 1 - Cánh Diều
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ cung cấp lời giải chi tiết cho từng câu hỏi:
Câu a: Tính limx→2 (x2 - 4) / (x - 2)
Lời giải:
- Phân tích tử số thành nhân tử: x2 - 4 = (x - 2)(x + 2)
- Rút gọn biểu thức: (x2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2
- Tính giới hạn: limx→2 (x + 2) = 2 + 2 = 4
Câu b: Tính limx→1 (x3 - 1) / (x - 1)
Lời giải:
- Phân tích tử số thành nhân tử: x3 - 1 = (x - 1)(x2 + x + 1)
- Rút gọn biểu thức: (x3 - 1) / (x - 1) = (x - 1)(x2 + x + 1) / (x - 1) = x2 + x + 1
- Tính giới hạn: limx→1 (x2 + x + 1) = 12 + 1 + 1 = 3
Lưu ý khi giải bài tập về giới hạn hàm số
- Luôn kiểm tra xem hàm số có liên tục tại điểm cần tính giới hạn hay không.
- Sử dụng các phương pháp giải phù hợp với từng dạng bài tập.
- Kiểm tra lại kết quả sau khi tính toán.
Tài liệu tham khảo thêm
Để nắm vững kiến thức về giới hạn hàm số, các em có thể tham khảo thêm các tài liệu sau:
- Sách giáo khoa Toán 12 tập 1 - Cánh Diều
- Sách bài tập Toán 12 tập 1 - Cánh Diều
- Các trang web học toán trực tuyến uy tín
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về cách giải bài tập 4 trang 13 SGK Toán 12 tập 1 - Cánh Diều. Chúc các em học tập tốt!