Giải mục 3 trang 71, 72, 73, 74, 75 SGK Toán 12 tập 2 - Cánh diều
Tổng quan nội dung
Giải mục 3 trang 71, 72, 73, 74, 75 SGK Toán 12 tập 2 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 71, 72, 73, 74, 75 SGK Toán 12 tập 2 - Cánh Diều. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục 3 này tập trung vào các kiến thức quan trọng của chương trình Toán 12, đòi hỏi các em phải nắm vững lý thuyết và kỹ năng giải bài tập.
Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Lấy hai đường thẳng \({\Delta _1},{\Delta _2}\) sao cho \({\Delta _1} \bot \left( {{P_1}} \right),\) \({\Delta _2} \bot \left( {{P_2}} \right)\) (Hình 31).
LT8
Trả lời câu hỏi Luyện tập 8 trang 74 SGK Toán 12 Cánh diều
Trong Ví dụ 10, tính góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính góc giữa hai mặt phẳng: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Lời giải chi tiết:
Vì ADD’A’ là hình vuông nên \(AD' \bot A'D\). Vì \(CD \bot \left( {ADD'A'} \right)\) nên \(CD \bot AD'\). Do đó, \(AD' \bot \left( {CDA'B'} \right)\).
Mặt khác, \(C'D' \bot \left( {BCC'B'} \right)\), suy ra góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’) là góc giữa hai đường thẳng AD’ và C’D’, đó là góc AD’C’.
Vì \(C'D' \bot \left( {ADD'A'} \right)\) nên \(C'D' \bot AD'\), suy ra . Do đó, góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’) bằng 90 độ.
LT9
Trả lời câu hỏi Luyện tập 9 trang 75 SGK Toán 12 Cánh diều
Cho mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\). Tính côsin của góc giữa mặt phẳng (P) và các mặt phẳng tọa độ.
Phương pháp giải:
Sử dụng kiến thức về côsin góc giữa hai mặt phẳng để tính: Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( {{P_1}} \right)\), \(\left( {{P_2}} \right)\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {{A_1};{B_1};{C_1}} \right)\), \(\overrightarrow {{n_2}} = \left( {{A_2};{B_2};{C_2}} \right)\). Khi đó, ta có: \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \frac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\sqrt {A_2^2 + B_2^2 + C_2^2} }}\).
Lời giải chi tiết:
Mặt phẳng (Oxy) có một vectơ pháp tuyến là \(\overrightarrow k = \left( {0;0;1} \right)\); mặt phẳng (Oxz) có một vectơ pháp tuyến là \(\overrightarrow j = \left( {0;1;0} \right)\); mặt phẳng (Oyz) có một vectơ pháp tuyến là \(\overrightarrow i = \left( {1;0;0} \right)\)
Do đó, \(\cos \left( {\left( {Oxy} \right),\left( P \right)} \right) = \frac{{\left| {0.A + 0.B + 1.C} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| C \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);
\(\cos \left( {\left( {Oxz} \right),\left( P \right)} \right) = \frac{{\left| {0.A + 1.B + 0.C} \right|}}{{\sqrt {{0^2} + {1^2} + {0^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| B \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);
\(\cos \left( {\left( {Oyz} \right),\left( P \right)} \right) = \frac{{\left| {1.A + 0.B + 0.C} \right|}}{{\sqrt {{1^2} + {0^2} + {0^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| A \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
HĐ8
Trả lời câu hỏi Hoạt động 8 trang 74 SGK Toán 12 Cánh diều
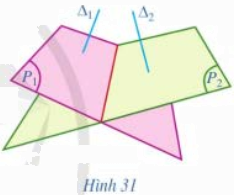
Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Lấy hai đường thẳng \({\Delta _1},{\Delta _2}\) sao cho \({\Delta _1} \bot \left( {{P_1}} \right),\) \({\Delta _2} \bot \left( {{P_2}} \right)\) (Hình 31).
 \
\
a) Nêu cách xác định góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\).
b) Góc đó có phụ thuộc vào việc chọn hai đường thẳng \({\Delta _1},{\Delta _2}\) như trên không?
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Góc giữa hai đường thẳng m và n trong không gian là góc giữa hai đường thẳng a và b cùng đi qua một điểm và tương ứng song song với m và n.
Lời giải chi tiết:
a) Vẽ hai đường thẳng \(\Delta _1',\Delta _2'\) cùng đi qua điểm I và lần lượt song song (hoặc trùng) với \({\Delta _1},{\Delta _2}\). Khi đó, góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) là góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\).
b) Vì \({\Delta _1} \bot \left( {{P_1}} \right)\) và \(\Delta _1'\) song song (hoặc trùng) với \({\Delta _1}\) nên \(\Delta _1' \bot \left( {{P_1}} \right)\).
Tương tự ta có: \(\Delta _2' \bot \left( {{P_2}} \right)\).
Khi đó, góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\) luôn là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) nên góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) không phụ thuộc vào việc chọn hai đường thẳng \({\Delta _1},{\Delta _2}\).
HĐ9
Trả lời câu hỏi Hoạt động 9 trang 75 SGK Toán 12 Cánh diều
Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Gọi \(\overrightarrow {{n_1}} = \left( {{A_1};{B_1};{C_1}} \right),\overrightarrow {{n_2}} = \left( {{A_2};{B_2};{C_2}} \right)\) lần lượt là hai vectơ pháp tuyến của \(\left( {{P_1}} \right)\), \(\left( {{P_2}} \right)\); \({\Delta _1},{\Delta _2}\) lần lượt là giá của hai vectơ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) (Hình 33). So sánh:

a) \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right)\) và \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\);
b) \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\) và \(\left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\).
Phương pháp giải:
Sử dụng kiến thức vectơ pháp tuyến của mặt phẳng để chứng minh: Nếu vectơ \(\overrightarrow n \) khác \(\overrightarrow 0 \) và có giá vuông góc với mặt phẳng (P) thì \(\overrightarrow n \) được gọi là vectơ pháp tuyến của mặt phẳng (P).
Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để chứng minh: Cho đường thẳng \(\Delta \) và vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \). Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).
Lời giải chi tiết:
a) Vì \({\Delta _1} \bot \left( {{P_1}} \right)\) nên đường thẳng \({\Delta _1}\) nhận một vectơ pháp tuyến \(\overrightarrow {{n_1}} \) của mặt phẳng \(\left( {{P_1}} \right)\) làm một vectơ chỉ phương.
Vì \({\Delta _2} \bot \left( {{P_2}} \right)\) nên đường thẳng \({\Delta _2}\) nhận một vectơ pháp tuyến \(\overrightarrow {{n_2}} \) của mặt phẳng \(\left( {{P_2}} \right)\) làm một vectơ chỉ phương.
Do đó, góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) là góc giữa hai vectơ pháp tuyến \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
Vậy \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \cos \left( {{\Delta _1},{\Delta _2}} \right)\).
b) Ta có:\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\).
- HĐ8
- LT8
- HĐ9
- LT9
Trả lời câu hỏi Hoạt động 8 trang 74 SGK Toán 12 Cánh diều
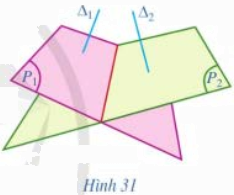
Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Lấy hai đường thẳng \({\Delta _1},{\Delta _2}\) sao cho \({\Delta _1} \bot \left( {{P_1}} \right),\) \({\Delta _2} \bot \left( {{P_2}} \right)\) (Hình 31).
 \
\
a) Nêu cách xác định góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\).
b) Góc đó có phụ thuộc vào việc chọn hai đường thẳng \({\Delta _1},{\Delta _2}\) như trên không?
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Góc giữa hai đường thẳng m và n trong không gian là góc giữa hai đường thẳng a và b cùng đi qua một điểm và tương ứng song song với m và n.
Lời giải chi tiết:
a) Vẽ hai đường thẳng \(\Delta _1',\Delta _2'\) cùng đi qua điểm I và lần lượt song song (hoặc trùng) với \({\Delta _1},{\Delta _2}\). Khi đó, góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) là góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\).
b) Vì \({\Delta _1} \bot \left( {{P_1}} \right)\) và \(\Delta _1'\) song song (hoặc trùng) với \({\Delta _1}\) nên \(\Delta _1' \bot \left( {{P_1}} \right)\).
Tương tự ta có: \(\Delta _2' \bot \left( {{P_2}} \right)\).
Khi đó, góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\) luôn là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) nên góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) không phụ thuộc vào việc chọn hai đường thẳng \({\Delta _1},{\Delta _2}\).
Trả lời câu hỏi Luyện tập 8 trang 74 SGK Toán 12 Cánh diều
Trong Ví dụ 10, tính góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính góc giữa hai mặt phẳng: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Lời giải chi tiết:
Vì ADD’A’ là hình vuông nên \(AD' \bot A'D\). Vì \(CD \bot \left( {ADD'A'} \right)\) nên \(CD \bot AD'\). Do đó, \(AD' \bot \left( {CDA'B'} \right)\).
Mặt khác, \(C'D' \bot \left( {BCC'B'} \right)\), suy ra góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’) là góc giữa hai đường thẳng AD’ và C’D’, đó là góc AD’C’.
Vì \(C'D' \bot \left( {ADD'A'} \right)\) nên \(C'D' \bot AD'\), suy ra . Do đó, góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’) bằng 90 độ.
Trả lời câu hỏi Hoạt động 9 trang 75 SGK Toán 12 Cánh diều
Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Gọi \(\overrightarrow {{n_1}} = \left( {{A_1};{B_1};{C_1}} \right),\overrightarrow {{n_2}} = \left( {{A_2};{B_2};{C_2}} \right)\) lần lượt là hai vectơ pháp tuyến của \(\left( {{P_1}} \right)\), \(\left( {{P_2}} \right)\); \({\Delta _1},{\Delta _2}\) lần lượt là giá của hai vectơ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) (Hình 33). So sánh:
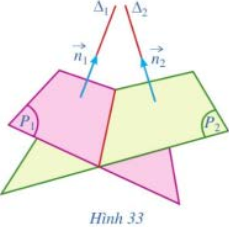
a) \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right)\) và \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\);
b) \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\) và \(\left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\).
Phương pháp giải:
Sử dụng kiến thức vectơ pháp tuyến của mặt phẳng để chứng minh: Nếu vectơ \(\overrightarrow n \) khác \(\overrightarrow 0 \) và có giá vuông góc với mặt phẳng (P) thì \(\overrightarrow n \) được gọi là vectơ pháp tuyến của mặt phẳng (P).
Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để chứng minh: Cho đường thẳng \(\Delta \) và vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \). Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).
Lời giải chi tiết:
a) Vì \({\Delta _1} \bot \left( {{P_1}} \right)\) nên đường thẳng \({\Delta _1}\) nhận một vectơ pháp tuyến \(\overrightarrow {{n_1}} \) của mặt phẳng \(\left( {{P_1}} \right)\) làm một vectơ chỉ phương.
Vì \({\Delta _2} \bot \left( {{P_2}} \right)\) nên đường thẳng \({\Delta _2}\) nhận một vectơ pháp tuyến \(\overrightarrow {{n_2}} \) của mặt phẳng \(\left( {{P_2}} \right)\) làm một vectơ chỉ phương.
Do đó, góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) là góc giữa hai vectơ pháp tuyến \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
Vậy \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \cos \left( {{\Delta _1},{\Delta _2}} \right)\).
b) Ta có:\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\).
Trả lời câu hỏi Luyện tập 9 trang 75 SGK Toán 12 Cánh diều
Cho mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\). Tính côsin của góc giữa mặt phẳng (P) và các mặt phẳng tọa độ.
Phương pháp giải:
Sử dụng kiến thức về côsin góc giữa hai mặt phẳng để tính: Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( {{P_1}} \right)\), \(\left( {{P_2}} \right)\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {{A_1};{B_1};{C_1}} \right)\), \(\overrightarrow {{n_2}} = \left( {{A_2};{B_2};{C_2}} \right)\). Khi đó, ta có: \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \frac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\sqrt {A_2^2 + B_2^2 + C_2^2} }}\).
Lời giải chi tiết:
Mặt phẳng (Oxy) có một vectơ pháp tuyến là \(\overrightarrow k = \left( {0;0;1} \right)\); mặt phẳng (Oxz) có một vectơ pháp tuyến là \(\overrightarrow j = \left( {0;1;0} \right)\); mặt phẳng (Oyz) có một vectơ pháp tuyến là \(\overrightarrow i = \left( {1;0;0} \right)\)
Do đó, \(\cos \left( {\left( {Oxy} \right),\left( P \right)} \right) = \frac{{\left| {0.A + 0.B + 1.C} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| C \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);
\(\cos \left( {\left( {Oxz} \right),\left( P \right)} \right) = \frac{{\left| {0.A + 1.B + 0.C} \right|}}{{\sqrt {{0^2} + {1^2} + {0^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| B \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);
\(\cos \left( {\left( {Oyz} \right),\left( P \right)} \right) = \frac{{\left| {1.A + 0.B + 0.C} \right|}}{{\sqrt {{1^2} + {0^2} + {0^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| A \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Giải mục 3 trang 71, 72, 73, 74, 75 SGK Toán 12 tập 2 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Mục 3 trong SGK Toán 12 tập 2 - Cánh Diều thường xoay quanh các chủ đề về Đường thẳng và Mặt phẳng trong không gian, bao gồm các kiến thức về vectơ, phương trình đường thẳng, phương trình mặt phẳng, và mối quan hệ giữa chúng. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán hình học không gian phức tạp hơn.
Nội dung chính của Mục 3
- Vectơ trong không gian: Định nghĩa, các phép toán vectơ (cộng, trừ, nhân với một số), tích vô hướng, tích có hướng và ứng dụng.
- Phương trình đường thẳng trong không gian: Các dạng phương trình (dạng tham số, dạng chính tắc, dạng phương trình tổng quát), điều kiện song song, vuông góc của hai đường thẳng.
- Phương trình mặt phẳng trong không gian: Dạng phương trình tổng quát, vectơ pháp tuyến, điều kiện song song, vuông góc của hai mặt phẳng, góc giữa đường thẳng và mặt phẳng.
- Khoảng cách: Khoảng cách từ một điểm đến mặt phẳng, khoảng cách giữa hai đường thẳng chéo nhau.
Giải chi tiết các bài tập trang 71, 72, 73, 74, 75
Dưới đây là giải chi tiết các bài tập trong Mục 3, trang 71, 72, 73, 74, 75 SGK Toán 12 tập 2 - Cánh Diều. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng để giúp các em hiểu sâu sắc kiến thức.
Bài 1 (Trang 71): ...
(Giải chi tiết bài 1 với đầy đủ các bước và giải thích)
Bài 2 (Trang 72): ...
(Giải chi tiết bài 2 với đầy đủ các bước và giải thích)
Bài 3 (Trang 73): ...
(Giải chi tiết bài 3 với đầy đủ các bước và giải thích)
Bài 4 (Trang 74): ...
(Giải chi tiết bài 4 với đầy đủ các bước và giải thích)
Bài 5 (Trang 75): ...
(Giải chi tiết bài 5 với đầy đủ các bước và giải thích)
Mẹo giải bài tập hiệu quả
- Nắm vững lý thuyết: Đảm bảo bạn hiểu rõ các định nghĩa, công thức và tính chất liên quan đến vectơ, đường thẳng và mặt phẳng.
- Vẽ hình: Vẽ hình minh họa giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Sử dụng các công cụ hỗ trợ: Sử dụng máy tính bỏ túi hoặc phần mềm hình học để kiểm tra lại kết quả.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục Toán học
Tusach.vn cam kết cung cấp cho bạn những lời giải chính xác, dễ hiểu và đầy đủ nhất. Hãy truy cập tusach.vn thường xuyên để cập nhật các bài giải mới nhất và nhận được sự hỗ trợ từ đội ngũ giáo viên giàu kinh nghiệm của chúng tôi. Chúc các em học tập tốt!
| Chủ đề | Nội dung chính |
|---|---|
| Vectơ | Định nghĩa, phép toán, tích vô hướng, tích có hướng |
| Đường thẳng | Phương trình, điều kiện song song, vuông góc |
| Mặt phẳng | Phương trình, vectơ pháp tuyến, điều kiện song song, vuông góc |