Giải mục 3 trang 54,55,56 SGK Toán 12 tập 2 - Cánh diều
Tổng quan nội dung
Giải mục 3 trang 54, 55, 56 SGK Toán 12 tập 2 - Cánh diều
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 54, 55, 56 SGK Toán 12 tập 2 - Cánh diều. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu nhất.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em giải quyết mọi khó khăn trong môn Toán.
Lập phương trình tổng quát của mặt phẳng biết một số điều kiện
HĐ7
Trả lời câu hỏi Hoạt động 7 trang 55 SGK Toán 12 Cánh diều
Cho ba điểm H(-1;1;2), I(1;3;2), K(-1;4;5) cùng thuộc mặt phẳng (P) (Hình 11)
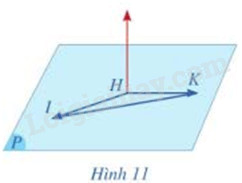
a) Tím tọa độ của các vecto \(\overrightarrow {HI} ,\overrightarrow {HK} \). Từ đó hãy chứng tỏ rằng ba điểm H, I, K không thẳng hàng
b) Lập phương trình mặt phẳng (P) đi qua điểm H(-1;1;2), biết cặp vecto chỉ phương là \(\overrightarrow {HI} ,\overrightarrow {HK} \)
Phương pháp giải:
a) \(A({a_1};{a_2};{a_3}),B({b_1};{b_2};{b_3}) \Rightarrow \overrightarrow {AB} = ({b_1} - {a_1};{b_2} - {a_2};{b_3} - {a_3})\)
b) Tìm vecto pháp tuyến của mặt phẳng \(\overrightarrow n = (A;B;C)\). Mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) và nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến có phương trình là \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
Lời giải chi tiết:
a) \(\overrightarrow {HI} = (2;2;0),\overrightarrow {HK} = (0;3;3)\)
Có \(\overrightarrow {HI} \ne k.\overrightarrow {HK} \) suy ra H, I, K không thẳng hàng
b) Vecto pháp tuyến của mặt phẳng (P) là: \(\overrightarrow n = [\overrightarrow {HI} ;\overrightarrow {HK} ] = (6; - 6;6)\)
Phương trình mặt phẳng (P) là: \(6(x + 1) - 6(y - 1) + 6(z - 2) = 0 \Leftrightarrow 6x - 6y + 6z = 0 \Leftrightarrow x - y + z = 0\)
HĐ6
Trả lời câu hỏi Hoạt động 6 trang 55 SGK Toán 12 Cánh diều
Cho mặt phẳng (P) đi qua điểm I(1;3;-2) có cặp vecto chỉ phương là \(\overrightarrow u = (1;1;3),\overrightarrow v = (2; - 1;2)\) (Hình 10)
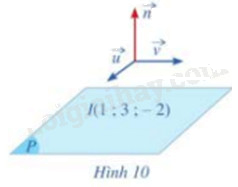
a) Hãy chỉ ra một vecto pháp tuyến \(\overrightarrow n \) của mặt phẳng (P)
b) Lập phương trình mặt phẳng (P) đi qua điểm I(1;3;-2) biết vecto pháp tuyển \(\overrightarrow n \)
Phương pháp giải:
a) Nếu hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) là cặp vecto chỉ phương của mặt phẳng (P) thì \(\overrightarrow n = [\overrightarrow u ;\overrightarrow v ] = \left( {\left| \begin{array}{l}{y_1}\;\;\;\;{z_1}\;\\{y_2}\;\;\;\;{z_2}\end{array} \right|;\left| \begin{array}{l}{z_1}\;\;\;\;{x_1}\\{x_2}\;\;\;\;{z_1}\end{array} \right|;\left| \begin{array}{l}{x_1}\;\;\;\;{y_1}\\{x_2}\;\;\;\;{y_2}\end{array} \right|} \right)\) là một vecto pháp tuyến của mặt phẳng (P)
b) Mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) và nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến có phương trình là \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
Lời giải chi tiết:
a) Vecto pháp tuyến của mặt phẳng (P) là \(\overrightarrow n = [\overrightarrow u ;\overrightarrow v ] = (5; - 4;3)\)
b) Phương trình mặt phẳng (P): \(5(x - 1) - 4(y - 3) + 3(z + 2) = 0 \Leftrightarrow 5x - 4y + 3z + 13 = 0\)
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 54 SGK Toán 12 Cánh diều
Cho mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) có \(\overrightarrow n (A;B;C)\) là vecto pháp tuyến. Giả sử M(x;y;z) là một điểm bất kì thuộc mặt phẳng (P) (Hình 9)
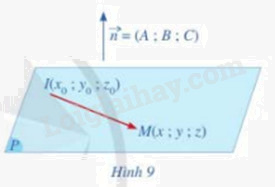
a) Tính tích vô hướng \(\overrightarrow n .\overrightarrow {IM} \)
b) Hãy biểu diễn \(\overrightarrow n .\overrightarrow {IM} \) theo \({x_0},{y_0},{z_0};x,y,z\) và A, B, C
Phương pháp giải:
Sử dụng công thức biểu thức tọa độ của tích vô hướng
Lời giải chi tiết:
a) \(\overrightarrow {IM} = (x - {x_0};y - {y_0};z - {z_0})\)
\(\overrightarrow n .\overrightarrow {IM} = A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0})\)
b) \(\overrightarrow n .\overrightarrow {IM} = A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = Ax + By + Cz - A{x_0} - B{y_0} - C{z_0}\)
- HĐ5
- HĐ6
- HĐ7
Trả lời câu hỏi Hoạt động 5 trang 54 SGK Toán 12 Cánh diều
Cho mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) có \(\overrightarrow n (A;B;C)\) là vecto pháp tuyến. Giả sử M(x;y;z) là một điểm bất kì thuộc mặt phẳng (P) (Hình 9)
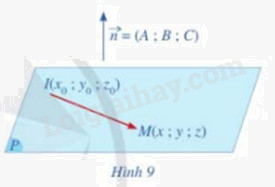
a) Tính tích vô hướng \(\overrightarrow n .\overrightarrow {IM} \)
b) Hãy biểu diễn \(\overrightarrow n .\overrightarrow {IM} \) theo \({x_0},{y_0},{z_0};x,y,z\) và A, B, C
Phương pháp giải:
Sử dụng công thức biểu thức tọa độ của tích vô hướng
Lời giải chi tiết:
a) \(\overrightarrow {IM} = (x - {x_0};y - {y_0};z - {z_0})\)
\(\overrightarrow n .\overrightarrow {IM} = A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0})\)
b) \(\overrightarrow n .\overrightarrow {IM} = A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = Ax + By + Cz - A{x_0} - B{y_0} - C{z_0}\)
Trả lời câu hỏi Hoạt động 6 trang 55 SGK Toán 12 Cánh diều
Cho mặt phẳng (P) đi qua điểm I(1;3;-2) có cặp vecto chỉ phương là \(\overrightarrow u = (1;1;3),\overrightarrow v = (2; - 1;2)\) (Hình 10)

a) Hãy chỉ ra một vecto pháp tuyến \(\overrightarrow n \) của mặt phẳng (P)
b) Lập phương trình mặt phẳng (P) đi qua điểm I(1;3;-2) biết vecto pháp tuyển \(\overrightarrow n \)
Phương pháp giải:
a) Nếu hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) là cặp vecto chỉ phương của mặt phẳng (P) thì \(\overrightarrow n = [\overrightarrow u ;\overrightarrow v ] = \left( {\left| \begin{array}{l}{y_1}\;\;\;\;{z_1}\;\\{y_2}\;\;\;\;{z_2}\end{array} \right|;\left| \begin{array}{l}{z_1}\;\;\;\;{x_1}\\{x_2}\;\;\;\;{z_1}\end{array} \right|;\left| \begin{array}{l}{x_1}\;\;\;\;{y_1}\\{x_2}\;\;\;\;{y_2}\end{array} \right|} \right)\) là một vecto pháp tuyến của mặt phẳng (P)
b) Mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) và nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến có phương trình là \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
Lời giải chi tiết:
a) Vecto pháp tuyến của mặt phẳng (P) là \(\overrightarrow n = [\overrightarrow u ;\overrightarrow v ] = (5; - 4;3)\)
b) Phương trình mặt phẳng (P): \(5(x - 1) - 4(y - 3) + 3(z + 2) = 0 \Leftrightarrow 5x - 4y + 3z + 13 = 0\)
Trả lời câu hỏi Hoạt động 7 trang 55 SGK Toán 12 Cánh diều
Cho ba điểm H(-1;1;2), I(1;3;2), K(-1;4;5) cùng thuộc mặt phẳng (P) (Hình 11)

a) Tím tọa độ của các vecto \(\overrightarrow {HI} ,\overrightarrow {HK} \). Từ đó hãy chứng tỏ rằng ba điểm H, I, K không thẳng hàng
b) Lập phương trình mặt phẳng (P) đi qua điểm H(-1;1;2), biết cặp vecto chỉ phương là \(\overrightarrow {HI} ,\overrightarrow {HK} \)
Phương pháp giải:
a) \(A({a_1};{a_2};{a_3}),B({b_1};{b_2};{b_3}) \Rightarrow \overrightarrow {AB} = ({b_1} - {a_1};{b_2} - {a_2};{b_3} - {a_3})\)
b) Tìm vecto pháp tuyến của mặt phẳng \(\overrightarrow n = (A;B;C)\). Mặt phẳng (P) đi qua điểm \(I({x_0};{y_0};{z_0})\) và nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến có phương trình là \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
Lời giải chi tiết:
a) \(\overrightarrow {HI} = (2;2;0),\overrightarrow {HK} = (0;3;3)\)
Có \(\overrightarrow {HI} \ne k.\overrightarrow {HK} \) suy ra H, I, K không thẳng hàng
b) Vecto pháp tuyến của mặt phẳng (P) là: \(\overrightarrow n = [\overrightarrow {HI} ;\overrightarrow {HK} ] = (6; - 6;6)\)
Phương trình mặt phẳng (P) là: \(6(x + 1) - 6(y - 1) + 6(z - 2) = 0 \Leftrightarrow 6x - 6y + 6z = 0 \Leftrightarrow x - y + z = 0\)
Giải mục 3 trang 54, 55, 56 SGK Toán 12 tập 2 - Cánh diều: Tổng quan và Hướng dẫn chi tiết
Mục 3 trong SGK Toán 12 tập 2 - Cánh diều thường xoay quanh các chủ đề về Số phức, bao gồm các khái niệm cơ bản, các phép toán trên số phức, và ứng dụng của số phức trong giải quyết các bài toán đại số và hình học. Việc nắm vững kiến thức này là vô cùng quan trọng để các em có thể tự tin làm bài kiểm tra và thi cử.
Nội dung chính của Mục 3
- Định nghĩa số phức: Số phức có dạng z = a + bi, trong đó a là phần thực và b là phần ảo.
- Các phép toán trên số phức: Cộng, trừ, nhân, chia số phức.
- Số phức liên hợp: Định nghĩa và tính chất của số phức liên hợp.
- Biểu diễn hình học của số phức: Biểu diễn số phức trên mặt phẳng phức.
- Ứng dụng của số phức: Giải phương trình bậc hai, phương trình bậc ba, và các bài toán hình học.
Giải chi tiết các bài tập trang 54, 55, 56
Bài 1: (Trang 54)
Bài 1 yêu cầu các em thực hiện các phép toán cộng, trừ, nhân, chia số phức. Để giải bài này, các em cần nắm vững các quy tắc về phép toán trên số phức. Ví dụ:
(a + bi) + (c + di) = (a + c) + (b + d)i
(a + bi) - (c + di) = (a - c) + (b - d)i
(a + bi)(c + di) = (ac - bd) + (ad + bc)i
...
Lời giải: (Giải chi tiết từng ý của bài 1 với các bước rõ ràng)
Bài 2: (Trang 55)
Bài 2 thường liên quan đến việc tìm số phức liên hợp. Các em cần nhớ rằng số phức liên hợp của z = a + bi là z' = a - bi.
Lời giải: (Giải chi tiết từng ý của bài 2 với các bước rõ ràng)
Bài 3: (Trang 56)
Bài 3 có thể yêu cầu các em biểu diễn số phức trên mặt phẳng phức hoặc giải phương trình bậc hai với hệ số phức. Để giải bài này, các em cần kết hợp kiến thức về số phức và hình học.
Lời giải: (Giải chi tiết từng ý của bài 3 với các bước rõ ràng)
Mẹo học tốt môn Toán 12
- Nắm vững kiến thức cơ bản: Đảm bảo các em hiểu rõ định nghĩa, tính chất và các quy tắc về số phức.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng tài liệu tham khảo: Tham khảo thêm các sách giáo trình, tài liệu ôn thi, và các trang web học tập trực tuyến.
- Hỏi thầy cô giáo: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo để được hướng dẫn và giải đáp.
Kết luận
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em sẽ tự tin hơn trong việc giải các bài tập mục 3 trang 54, 55, 56 SGK Toán 12 tập 2 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao!
Tusach.vn – Luôn đồng hành cùng các em trên con đường chinh phục tri thức!