Giải bài tập 3 trang 39 SGK Toán 12 tập 2 - Cánh diều
Tổng quan nội dung
Giải bài tập 3 trang 39 SGK Toán 12 tập 2 - Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài tập 3 trang 39 SGK Toán 12 tập 2 - Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12 tập 2 - Cánh Diều, đáp ứng nhu cầu học tập của học sinh.
Cho đồ thị hàm số (y = {e^x}) và hình phẳng được tô màu như Hình 29 a) Hình phẳng đó được giới hạn bởi các đường nào? b) Tính diện tích hình phẳng đó
Đề bài
Cho đồ thị hàm số \(y = {e^x}\) và hình phẳng được tô màu như Hình 29
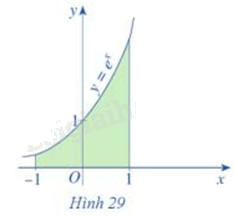
a) Hình phẳng đó được giới hạn bởi các đường nào?
b) Tính diện tích hình phẳng đó
Phương pháp giải - Xem chi tiết
a) Quan sát hình vẽ
b) Cho hàm số y = f(x), y = g(x) liên tục trên đoạn [a;b]. Khi đó, diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b là: \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \)
Lời giải chi tiết
a) Hình phẳng đó được giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục Ox, đường thẳng x = -1 và x = 1
b) Diện tích hình phẳng đó là: \(S = \int\limits_{ - 1}^1 {{e^x}} dx = \left. {{e^x}} \right|_{ - 1}^1 = e - \frac{1}{e}\)
Giải bài tập 3 trang 39 SGK Toán 12 tập 2 - Cánh Diều: Tổng quan và hướng dẫn chi tiết
Bài tập 3 trang 39 SGK Toán 12 tập 2 - Cánh Diều thuộc chương trình học Toán 12, tập trung vào kiến thức về Đạo hàm của hàm số hợp. Đây là một phần quan trọng trong chương trình, giúp học sinh hiểu rõ hơn về các ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
Nội dung bài tập 3 trang 39 SGK Toán 12 tập 2 - Cánh Diều
Bài tập 3 yêu cầu học sinh tính đạo hàm của các hàm số hợp. Để giải bài tập này, học sinh cần nắm vững các quy tắc tính đạo hàm, đặc biệt là quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x).
Hướng dẫn giải chi tiết bài tập 3 trang 39 SGK Toán 12 tập 2 - Cánh Diều
Dưới đây là hướng dẫn giải chi tiết từng câu của bài tập 3:
- Câu a: y = sin(x2 + 1)
- Câu b: y = cos(2x + 3)
- Câu c: y = tan(x3)
- Câu d: y = cot(sin x)
Để giải câu này, ta đặt u = x2 + 1 và y = sin(u). Khi đó, u' = 2x và y' = cos(u). Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = cos(x2 + 1) * 2x = 2x * cos(x2 + 1)
Tương tự như câu a, ta đặt u = 2x + 3 và y = cos(u). Khi đó, u' = 2 và y' = -sin(u). Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = -sin(2x + 3) * 2 = -2sin(2x + 3)
Đặt u = x3 và y = tan(u). Khi đó, u' = 3x2 và y' = sec2(u). Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = sec2(x3) * 3x2 = 3x2 * sec2(x3)
Đặt u = sin x và y = cot(u). Khi đó, u' = cos x và y' = -csc2(u). Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = -csc2(sin x) * cos x = -cos x * csc2(sin x)
Lưu ý khi giải bài tập về đạo hàm hàm số hợp
- Xác định đúng hàm trong và hàm ngoài.
- Tính đạo hàm của từng hàm một cách chính xác.
- Áp dụng quy tắc đạo hàm của hàm hợp một cách cẩn thận.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài tập tương tự và luyện tập thêm
Để củng cố kiến thức về đạo hàm hàm số hợp, bạn có thể luyện tập thêm các bài tập tương tự sau:
| Bài tập | Lời giải |
|---|---|
| Tính đạo hàm của y = sin2(x) | y' = 2sin(x)cos(x) |
| Tính đạo hàm của y = ex2 | y' = 2xex2 |
Tusach.vn hy vọng với hướng dẫn chi tiết này, bạn sẽ giải quyết thành công bài tập 3 trang 39 SGK Toán 12 tập 2 - Cánh Diều và nắm vững kiến thức về đạo hàm hàm số hợp. Chúc bạn học tập tốt!