Giải bài tập 4 trang 39 SGK Toán 12 tập 2 - Cánh diều
Tổng quan nội dung
Giải bài tập 4 trang 39 SGK Toán 12 tập 2 - Cánh diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 4 trang 39 SGK Toán 12 tập 2 - Cánh diều. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em tự tin hơn trong quá trình học tập môn Toán.
tusach.vn luôn đồng hành cùng các em học sinh, cung cấp tài liệu học tập chất lượng và hỗ trợ tối đa cho việc ôn luyện và làm bài tập.
Cho đồ thị các hàm số (y = {left( {frac{1}{2}} right)^x}), y = x + 1 và hình phẳng được tô màu như hình 30 a) Hình phẳng đó được giới hạn bởi các đường nào? b) Tính diện tích hình phẳng đó
Đề bài
Cho đồ thị các hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\), y = x + 1 và hình phẳng được tô màu như hình 30
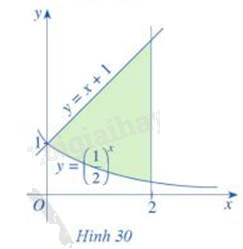
a) Hình phẳng đó được giới hạn bởi các đường nào?
b) Tính diện tích hình phẳng đó
Phương pháp giải - Xem chi tiết
a) Quan sát hình vẽ
b) Cho hàm số y = f(x), y = g(x) liên tục trên đoạn [a;b]. Khi đó, diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b là: \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \)
Lời giải chi tiết
a) Hình phẳng đó được giới hạn bởi đồ thị hàm số y = x + 1, \(y = {\left( {\frac{1}{2}} \right)^x}\), đường thẳng x = 0 và x = 2
b) Diện tích hình phẳng đó là: \(S = \int\limits_0^2 {\left| {x + 1 - {{\left( {\frac{1}{2}} \right)}^x}} \right|} dx = \int\limits_0^2 {\left( {x + 1 - {{\left( {\frac{1}{2}} \right)}^x}} \right)} dx = \left. {\left( {\frac{{{x^2}}}{2} + x - \frac{{{{\left( {\frac{1}{2}} \right)}^x}}}{{ - \ln 2}}} \right)} \right|_0^2 \approx 2,92\)
Giải bài tập 4 trang 39 SGK Toán 12 tập 2 - Cánh diều: Tổng quan và Phương pháp giải
Bài tập 4 trang 39 SGK Toán 12 tập 2 - Cánh diều thuộc chương trình học về Đạo hàm của hàm số hợp. Đây là một phần kiến thức quan trọng, thường xuyên xuất hiện trong các đề thi. Để giải quyết bài tập này một cách hiệu quả, các em cần nắm vững các kiến thức cơ bản về đạo hàm, quy tắc đạo hàm của hàm hợp và các công thức liên quan.
Nội dung bài tập 4 trang 39 SGK Toán 12 tập 2 - Cánh diều
Bài tập 4 yêu cầu các em tính đạo hàm của các hàm số được cho. Các hàm số này thường có dạng phức tạp, đòi hỏi các em phải áp dụng linh hoạt các quy tắc đạo hàm và biến đổi đại số để đưa về dạng đơn giản hơn.
Lời giải chi tiết bài tập 4 trang 39 SGK Toán 12 tập 2 - Cánh diều
Dưới đây là lời giải chi tiết cho từng câu của bài tập 4:
Câu a:
Cho hàm số y = sin(x2 + 1). Tính y'.
Lời giải:
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = cos(x2 + 1) * (x2 + 1)' = cos(x2 + 1) * 2x = 2x * cos(x2 + 1)
Câu b:
Cho hàm số y = ecos x. Tính y'.
Lời giải:
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = ecos x * (cos x)' = ecos x * (-sin x) = -sin x * ecos x
Câu c:
Cho hàm số y = ln(x2 + 1). Tính y'.
Lời giải:
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = (ln(x2 + 1))' = (1/(x2 + 1)) * (x2 + 1)' = (1/(x2 + 1)) * 2x = 2x/(x2 + 1)
Mẹo giải nhanh bài tập về đạo hàm hàm hợp
- Nắm vững quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x)
- Phân tích hàm số: Xác định hàm ngoài (u) và hàm trong (v) để áp dụng quy tắc một cách chính xác.
- Biến đổi đại số: Đơn giản hóa biểu thức đạo hàm sau khi áp dụng quy tắc.
- Kiểm tra lại kết quả: Đảm bảo kết quả đạo hàm phù hợp với hàm số ban đầu.
Bài tập tương tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
- Tính đạo hàm của hàm số y = cos(ex).
- Tính đạo hàm của hàm số y = ln(sin x).
- Tính đạo hàm của hàm số y = tan(x3).
Kết luận
Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên, các em đã nắm vững cách giải bài tập 4 trang 39 SGK Toán 12 tập 2 - Cánh diều. Hãy luyện tập thường xuyên để nâng cao kỹ năng giải toán và đạt kết quả tốt nhất trong các kỳ thi.
tusach.vn luôn sẵn sàng hỗ trợ các em trên con đường chinh phục tri thức. Chúc các em học tập tốt!