Giải mục 3 trang 24, 25, 26 SGK Toán 12 tập 1 - Cánh diều
Tổng quan nội dung
Giải mục 3 trang 24, 25, 26 SGK Toán 12 tập 1 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 24, 25, 26 SGK Toán 12 tập 1 chương trình Cánh Diều. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em hiểu rõ kiến thức và tự tin giải quyết các bài toán.
Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để các em có thể nắm vững kiến thức và áp dụng vào các bài tập tương tự.
Đường tiệm cận xiên
LT3
Trả lời câu hỏi Luyện tập 3 trang 25SGK Toán 12 Cánh diều
Chứng minh rằng đường thẳng \(y = - x\) là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}\).
Phương pháp giải:
Đưởng thẳng \(y = ax + b\left( {a \ne 0} \right)\) được gọi là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}} = - x + \frac{3}{{x + 2}}\).
Xét \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( { - x} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{3}{{x + 2}} = 0\).
Vậy đường thẳng \(y = - x\) là đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}\)
LT4
Trả lời câu hỏi Luyện tập 4 trang 26SGK Toán 12 Cánh diều
Tìm tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\).
Phương pháp giải:
Đưởng thẳng \(y = ax + b\left( {a \ne 0} \right)\) được gọi là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}} = x - 6 + \frac{{20}}{{x + 3}}\).
Xét \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 6} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{20}}{{x + 3}} = 0\).
Vậy đường thẳng \(y = x - 6\) là đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\)
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 24SGK Toán 12 Cánh diều
Cho hàm số \(y = f\left( x \right) = x + 1 + \frac{1}{{x - 1}}\) có đồ thị \(\left( C \right)\) và đường thẳng \(y = x + 1\) (Hình 15). Tìm \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right];\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right]\)
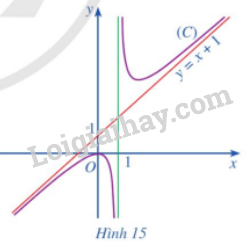
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 1}} = 0\\\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 1}} = 0\end{array} \right.\)
- HĐ3
- LT3
- LT4
Trả lời câu hỏi Hoạt động 3 trang 24SGK Toán 12 Cánh diều
Cho hàm số \(y = f\left( x \right) = x + 1 + \frac{1}{{x - 1}}\) có đồ thị \(\left( C \right)\) và đường thẳng \(y = x + 1\) (Hình 15). Tìm \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right];\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right]\)
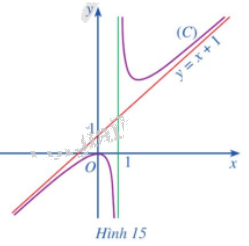
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 1}} = 0\\\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 1}} = 0\end{array} \right.\)
Trả lời câu hỏi Luyện tập 3 trang 25SGK Toán 12 Cánh diều
Chứng minh rằng đường thẳng \(y = - x\) là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}\).
Phương pháp giải:
Đưởng thẳng \(y = ax + b\left( {a \ne 0} \right)\) được gọi là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}} = - x + \frac{3}{{x + 2}}\).
Xét \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( { - x} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{3}{{x + 2}} = 0\).
Vậy đường thẳng \(y = - x\) là đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}\)
Trả lời câu hỏi Luyện tập 4 trang 26SGK Toán 12 Cánh diều
Tìm tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\).
Phương pháp giải:
Đưởng thẳng \(y = ax + b\left( {a \ne 0} \right)\) được gọi là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - \left( {ax + b} \right)} \right] = 0\).
Lời giải chi tiết:
Ta có: \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}} = x - 6 + \frac{{20}}{{x + 3}}\).
Xét \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - \left( {x - 6} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{20}}{{x + 3}} = 0\).
Vậy đường thẳng \(y = x - 6\) là đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\)
Giải mục 3 trang 24, 25, 26 SGK Toán 12 tập 1 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Mục 3 trong SGK Toán 12 tập 1 chương trình Cánh Diều tập trung vào việc nghiên cứu về đạo hàm của hàm số lượng giác. Đây là một phần kiến thức quan trọng, nền tảng cho việc giải quyết nhiều bài toán trong chương trình Toán 12 và các kỳ thi quan trọng như THPT Quốc gia. Bài viết này sẽ cung cấp lời giải chi tiết cho các bài tập trang 24, 25, 26, giúp các em hiểu rõ bản chất của vấn đề và rèn luyện kỹ năng giải toán.
Nội dung chính của Mục 3
- Công thức đạo hàm của các hàm số lượng giác cơ bản: sin(x), cos(x), tan(x), cot(x).
- Các quy tắc tính đạo hàm: Quy tắc cộng, trừ, nhân, chia, quy tắc hàm hợp.
- Ứng dụng của đạo hàm trong việc giải các bài toán liên quan đến hàm số lượng giác: Tìm cực trị, khảo sát hàm số, giải phương trình, bất phương trình.
Giải chi tiết các bài tập trang 24, 25, 26
Bài 1: Tính đạo hàm của các hàm số sau
- y = sin(2x)
- y = cos(x^2)
- y = tan(3x + 1)
Lời giải:
- y = sin(2x) => y' = cos(2x) * 2 = 2cos(2x) (Sử dụng quy tắc hàm hợp)
- y = cos(x^2) => y' = -sin(x^2) * 2x = -2xsin(x^2) (Sử dụng quy tắc hàm hợp)
- y = tan(3x + 1) => y' = (1/cos^2(3x+1)) * 3 = 3/(cos^2(3x+1)) (Sử dụng quy tắc hàm hợp và công thức đạo hàm của tan(x))
Bài 2: Tìm đạo hàm cấp hai của hàm số y = sin(x)cos(x)
Lời giải:
y' = cos(x)cos(x) + sin(x)(-sin(x)) = cos^2(x) - sin^2(x) = cos(2x)
y'' = -2sin(2x)
Bài 3: Cho hàm số y = x^2 + sin(x). Tìm y' và y''
Lời giải:
y' = 2x + cos(x)
y'' = 2 - sin(x)
Mẹo giải toán đạo hàm hàm số lượng giác
- Nắm vững các công thức đạo hàm cơ bản: Đây là nền tảng để giải quyết mọi bài toán.
- Sử dụng quy tắc hàm hợp một cách linh hoạt: Quy tắc này thường xuyên xuất hiện trong các bài toán đạo hàm hàm số lượng giác.
- Biến đổi biểu thức lượng giác: Đôi khi, việc biến đổi biểu thức lượng giác có thể giúp đơn giản hóa bài toán.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tài liệu tham khảo thêm
Ngoài SGK Toán 12 tập 1 Cánh Diều, các em có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 12
- Các trang web học Toán trực tuyến uy tín
- Các video hướng dẫn giải Toán trên YouTube
Hy vọng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong Mục 3 trang 24, 25, 26 SGK Toán 12 tập 1 chương trình Cánh Diều. Chúc các em học tập tốt!