Giải mục 1 trang 28,29,30 SGK Toán 12 tập 2 - Cánh diều
Tổng quan nội dung
Giải mục 1 trang 28,29,30 SGK Toán 12 tập 2 - Cánh diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 28, 29, 30 SGK Toán 12 tập 2 chương trình Cánh diều. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em hiểu rõ kiến thức và tự tin giải quyết các bài toán.
Bài tập trong mục này tập trung vào các kiến thức về đạo hàm của hàm số, bao gồm các dạng bài tập tính đạo hàm, xét tính đơn điệu của hàm số và tìm cực trị.
Tính diện tích hình phẳng
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 28 SGK Toán 12 Cánh diều
Cho hàm số \(y = f(x) = {x^3} - 2{x^2} - x + 2\) có đồ thị minh họa ở Hình 11.

a) Quan sát Hình 11, hãy cho biết các hình phẳng \({H_1},{H_2},{H_3}\) lần lượt được giới hạn bởi các đường thẳng và đồ thị hàm số nào
b) Tính diện tích \({S_{{H_1}}},{S_{{H_2}}},{S_{{H_3}}}\) của các hình phẳng đó
c) Gọi H là tập hợp của các hình phẳng \({H_1},{H_2},{H_3}\). Hình phẳng H được gọi là hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và các đường thẳng x = 0, x = 3. Chứng tỏ rằng diện tích \({S_H}\) của hình phẳng H bằng \({S_H} = {S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} = \int\limits_0^3 {\left| {f(x)} \right|dx} \)
Phương pháp giải:
a) Quan sát hình vẽ
b) Sử dụng công thức tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b là: \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)
c) Sử dụng tính chất của tích phân \(\int\limits_a^b {f(x)} dx = \int\limits_a^c {f(x)} dx + \int\limits_c^b {f(x)} dx\)
Lời giải chi tiết:
a) Hình \({H_1}\) được giới hạn bởi các đường thẳng x = 0, x = 1 và đồ thị hàm số y = f(x)
Hình \({H_2}\) được giới hạn bởi các đường thẳng x = 1, x = 2 và đồ thị hàm số y = f(x)
Hình \({H_3}\) được giới hạn bởi các đường thẳng x = 2, x = 3 và đồ thị hàm số y = f(x)
b) \({S_{{H_1}}} = \int\limits_0^1 {f(x)dx} = \int\limits_0^1 {\left( {{x^3} - 2{x^2} - x + 2} \right)dx} = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_0^1 = \frac{{13}}{{12}}\)
\(\int\limits_1^2 {f(x)dx = \int\limits_1^2 {\left( {{x^3} - 2{x^2} - x + 2} \right)} } dx = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_1^2 = - \frac{5}{{12}} \to {S_{{H_2} = }}\frac{5}{{12}}\)
\({S_{{H_3}}} = \int\limits_2^3 {f(x)dx = \int\limits_2^3 {\left( {{x^3} - 2{x^2} - x + 2} \right)} } dx = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_2^3 = \frac{{37}}{{12}}\)
c) \({S_H} = {S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} = \int\limits_0^1 {f(x)dx} + \left| {\int\limits_1^2 {f(x)dx} } \right| + \int\limits_2^3 {f(x)dx} = \int\limits_0^3 {\left| {f(x)} \right|dx} \)
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 30 SGK Toán 12 Cánh diều
Cho các hàm số \(y = {2^x}\), y = x
Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số \(y = {2^x}\)
Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số y = x
Gọi S là phẳng giới hạn bởi các đồ thị hàm số \(y = {2^x}\), y = x và hai đường thẳng x = 1, x = 2
(Hình 14)
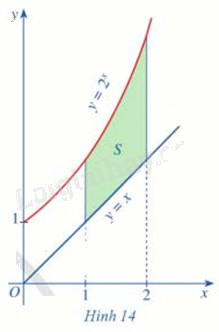
a) Biểu diễn S theo \({S_1},{S_2}\)
b) So sánh S và \(\int\limits_1^2 {({2^x} - x)dx} \)
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
a) \(S = {S_1} - {S_2}\)
b) \(S = {S_1} - {S_2}\)
\(\int\limits_1^2 {({2^x} - x)dx} = \int\limits_1^2 {{2^x}dx} - \int\limits_1^2 {xdx} = {S_1} - {S_2}\)
Vậy S = \(\int\limits_1^2 {({2^x} - x)dx} \)
- HĐ1
- HĐ2
Trả lời câu hỏi Hoạt động 1 trang 28 SGK Toán 12 Cánh diều
Cho hàm số \(y = f(x) = {x^3} - 2{x^2} - x + 2\) có đồ thị minh họa ở Hình 11.

a) Quan sát Hình 11, hãy cho biết các hình phẳng \({H_1},{H_2},{H_3}\) lần lượt được giới hạn bởi các đường thẳng và đồ thị hàm số nào
b) Tính diện tích \({S_{{H_1}}},{S_{{H_2}}},{S_{{H_3}}}\) của các hình phẳng đó
c) Gọi H là tập hợp của các hình phẳng \({H_1},{H_2},{H_3}\). Hình phẳng H được gọi là hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và các đường thẳng x = 0, x = 3. Chứng tỏ rằng diện tích \({S_H}\) của hình phẳng H bằng \({S_H} = {S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} = \int\limits_0^3 {\left| {f(x)} \right|dx} \)
Phương pháp giải:
a) Quan sát hình vẽ
b) Sử dụng công thức tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b là: \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)
c) Sử dụng tính chất của tích phân \(\int\limits_a^b {f(x)} dx = \int\limits_a^c {f(x)} dx + \int\limits_c^b {f(x)} dx\)
Lời giải chi tiết:
a) Hình \({H_1}\) được giới hạn bởi các đường thẳng x = 0, x = 1 và đồ thị hàm số y = f(x)
Hình \({H_2}\) được giới hạn bởi các đường thẳng x = 1, x = 2 và đồ thị hàm số y = f(x)
Hình \({H_3}\) được giới hạn bởi các đường thẳng x = 2, x = 3 và đồ thị hàm số y = f(x)
b) \({S_{{H_1}}} = \int\limits_0^1 {f(x)dx} = \int\limits_0^1 {\left( {{x^3} - 2{x^2} - x + 2} \right)dx} = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_0^1 = \frac{{13}}{{12}}\)
\(\int\limits_1^2 {f(x)dx = \int\limits_1^2 {\left( {{x^3} - 2{x^2} - x + 2} \right)} } dx = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_1^2 = - \frac{5}{{12}} \to {S_{{H_2} = }}\frac{5}{{12}}\)
\({S_{{H_3}}} = \int\limits_2^3 {f(x)dx = \int\limits_2^3 {\left( {{x^3} - 2{x^2} - x + 2} \right)} } dx = \left. {\left( {\frac{{{x^4}}}{4} - \frac{2}{3}{x^3} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_2^3 = \frac{{37}}{{12}}\)
c) \({S_H} = {S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} = \int\limits_0^1 {f(x)dx} + \left| {\int\limits_1^2 {f(x)dx} } \right| + \int\limits_2^3 {f(x)dx} = \int\limits_0^3 {\left| {f(x)} \right|dx} \)
Trả lời câu hỏi Hoạt động 2 trang 30 SGK Toán 12 Cánh diều
Cho các hàm số \(y = {2^x}\), y = x
Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số \(y = {2^x}\)
Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số y = x
Gọi S là phẳng giới hạn bởi các đồ thị hàm số \(y = {2^x}\), y = x và hai đường thẳng x = 1, x = 2
(Hình 14)
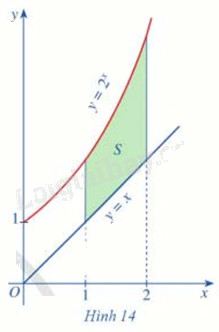
a) Biểu diễn S theo \({S_1},{S_2}\)
b) So sánh S và \(\int\limits_1^2 {({2^x} - x)dx} \)
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
a) \(S = {S_1} - {S_2}\)
b) \(S = {S_1} - {S_2}\)
\(\int\limits_1^2 {({2^x} - x)dx} = \int\limits_1^2 {{2^x}dx} - \int\limits_1^2 {xdx} = {S_1} - {S_2}\)
Vậy S = \(\int\limits_1^2 {({2^x} - x)dx} \)
Giải mục 1 trang 28,29,30 SGK Toán 12 tập 2 - Cánh diều: Tổng quan và hướng dẫn giải chi tiết
Mục 1 trang 28, 29, 30 SGK Toán 12 tập 2 Cánh diều là một phần quan trọng trong chương trình học, tập trung vào việc củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Để giúp các em học sinh nắm vững kiến thức và tự tin làm bài, tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho từng bài tập trong mục này.
Nội dung chính của mục 1 trang 28,29,30
- Bài 1: Tính đạo hàm của các hàm số sau:
- a) y = x3 - 3x2 + 2x - 5
- b) y = (x2 + 1)(x - 2)
- c) y = (x + 1) / (x - 1)
- Bài 2: Tìm đạo hàm của hàm số y = sin(2x + 1)
- Bài 3: Cho hàm số y = x4 - 4x3 + 4x2 + 1. Tìm các điểm cực trị của hàm số.
- Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = x3 - 3x + 2
Hướng dẫn giải chi tiết
Bài 1: Để tính đạo hàm của các hàm số, chúng ta sử dụng các quy tắc đạo hàm cơ bản như quy tắc đạo hàm của tổng, tích, thương và quy tắc đạo hàm của hàm hợp.
Ví dụ, để tính đạo hàm của hàm số y = x3 - 3x2 + 2x - 5, ta áp dụng quy tắc đạo hàm của tổng và quy tắc đạo hàm của lũy thừa:
y' = 3x2 - 6x + 2
Bài 2: Để tìm đạo hàm của hàm số y = sin(2x + 1), ta sử dụng quy tắc đạo hàm của hàm hợp:
y' = cos(2x + 1) * 2 = 2cos(2x + 1)
Bài 3: Để tìm các điểm cực trị của hàm số y = x4 - 4x3 + 4x2 + 1, ta thực hiện các bước sau:
- Tính đạo hàm bậc nhất y' = 4x3 - 12x2 + 8x
- Giải phương trình y' = 0 để tìm các điểm dừng: 4x3 - 12x2 + 8x = 0 => x = 0, x = 1, x = 2
- Tính đạo hàm bậc hai y'' = 12x2 - 24x + 8
- Kiểm tra dấu của y'' tại các điểm dừng để xác định điểm cực đại, cực tiểu:
- y''(0) = 8 > 0 => x = 0 là điểm cực tiểu
- y''(1) = -4 < 0 => x = 1 là điểm cực đại
- y''(2) = 8 > 0 => x = 2 là điểm cực tiểu
Bài 4: Để khảo sát sự biến thiên và vẽ đồ thị của hàm số y = x3 - 3x + 2, ta thực hiện các bước sau:
- Xác định tập xác định: D = R
- Tính đạo hàm bậc nhất y' = 3x2 - 3
- Giải phương trình y' = 0 để tìm các điểm dừng: 3x2 - 3 = 0 => x = 1, x = -1
- Lập bảng biến thiên
- Vẽ đồ thị
Lời khuyên khi học tập
Để học tốt môn Toán 12, các em cần:
- Nắm vững kiến thức cơ bản về đạo hàm và ứng dụng của đạo hàm.
- Luyện tập thường xuyên các bài tập để rèn luyện kỹ năng giải toán.
- Tìm hiểu các phương pháp giải toán khác nhau để có thể áp dụng vào các bài toán cụ thể.
- Tham khảo các tài liệu học tập và lời giải chi tiết trên tusach.vn.
Tusach.vn hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập này, các em sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán 12.