Giải mục 3 trang 8, 9, 10 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải Mục 3 Trang 8, 9, 10 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết Mục 3 trang 8, 9, 10 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em hiểu rõ kiến thức và tự tin giải quyết các bài tập.
Bài viết này sẽ cung cấp đáp án và phương pháp giải các bài tập trong Mục 3, giúp các em củng cố kiến thức về các khái niệm và định lý đã học.
Trong mỗi trường hợp dưới đây, cho f là một phép dời hình.
Thực hành 3
Gọi A’B’C’D’ là ảnh của hình chữ nhật ABCD qua phép biến hình được diễn tả trong Vận dụng. Hãy cho biết A’B’C’D’ là hình gì. Giải thích.
Phương pháp giải:
Phép dời hình bảo toàn:
- Tính thẳng hàng của 3 điểm và thứ tự của ba điểm thẳng hàng.
- Tính song song của hai đường thẳng.
- Độ lớn của một góc.
Lời giải chi tiết:
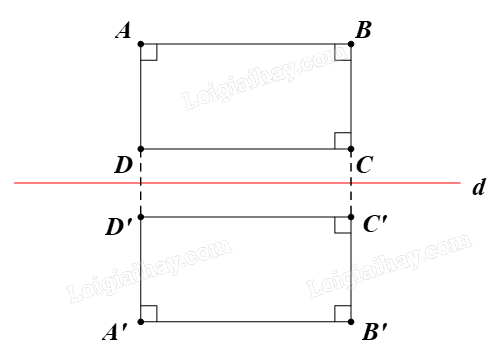
Gọi f là phép biến hình trong Vận dụng.
Trong Vận dụng, ta đã chứng minh được f là một phép dời hình.
Ta có ABCD là hình chữ nhật.
Suy ra \(\;\widehat {DAB} = 90^\circ ;\,\,\widehat {ABC} = 90^\circ ;\,\,\widehat {BCD} = 90^\circ \)
Do phép dời hình f bảo toàn độ lớn của góc nên ta có \(\widehat {{\rm{D'A'B'}}} = 90^\circ ;\widehat {{\rm{A'B'C'}}} = 90^\circ ;\widehat {{\rm{B'C'D'}}} = 90^\circ \)
Vậy A’B’C’D’ cũng là hình chữ nhật.
Khám phá 3
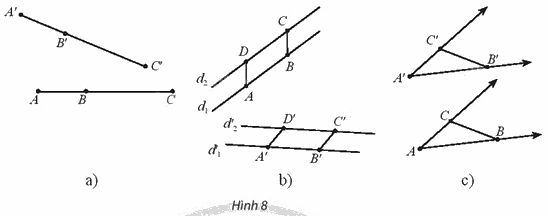
Trong mỗi trường hợp dưới đây, cho f là một phép dời hình.
a) Cho ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C). Gọi A’, B’, C’ lần lượt là ảnh của A, B, C qua f (Hình 8a). Có nhận xét gì về vị trí tương đối của ba điểm A’, B’, C’?
b) Cho hai đường thẳng song song d1 và d2, lấy hai đoạn thẳng bằng nhau AB và DC lần lượt trên d1 và d2. Gọi \({d_1}',{d_2}'\) lần lượt là ảnh của d1, d2 và A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua f (Hình 8b). Tứ giác A’B’C’D’ là hình gì? Nêu nhận xét về vị trí tương đối của hai đường thẳng \({d_1}',{d_2}'\).
c) Cho A’B’C’ là ảnh của tam giác ABC qua f (Hình 8c).
So sánh và \(\Delta ABC\). So sánh số đo hai góc \(\widehat {BAC}\) và \(\widehat {B'A'C'}\).
Phương pháp giải:
Quan sát hình 8 để trả lời
Lời giải chi tiết:
Phép dời hình f bảo toàn khoảng cách giữa hai điểm bất kì.
a) Ta có A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.
Suy ra A’B’ = AB; B’C’ = BC và A’C’ = AC.
Theo đề, ta có ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C).
Suy ra AB + BC = AC.
Khi đó A’B’ + B’C’ = A’C’.
Vậy ba điểm A’, B’, C’ thẳng hàng theo thứ tự (B’ nằm giữa A’ và C’).
b) Ta có AB = DC (giả thiết) và AB // DC (do d1 // d2).
Suy ra tứ giác ABCD là hình bình hành.
Khi đó AD = BC.
Ta có A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua phép dời hình f.
Suy ra A’B’ = AB; D’C’ = DC.
Mà AB = DC (giả thiết), do đó A’B’ = D’C’ (1)
Chứng minh tương tự, ta được A’D’ = B’C’ (2)
Từ (1), (2), suy ra tứ giác A’B’C’D’ là hình bình hành.
Khi đó A’B’ // D’C’ hay \({d_1}'{\rm{//}}{d_2}'\).
Vậy tứ giác A’B’C’D’ là hình bình hành và \({d_1}'{\rm{//}}{d_2}'\).
c) Ta có tam giác A’B’C’ là ảnh của tam giác ABC qua phép dời hình f.
Suy ra A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.
Vì vậy A’B’ = AB; B’C’ = BC và A’C’ = AC.
Do đó ∆A’B’C’ = ∆ABC (c.c.c).
Từ đó suy ra \(\widehat {B'A'C'} = \widehat {BAC}\) (cặp cạnh tương ứng).
Vậy \(\Delta A'B'C'{\rm{ }} = {\rm{ }}\Delta ABC\) và \(\widehat {B'A'C'} = \widehat {BAC}\).
- Khám phá 3
- Thực hành 3
Trong mỗi trường hợp dưới đây, cho f là một phép dời hình.
a) Cho ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C). Gọi A’, B’, C’ lần lượt là ảnh của A, B, C qua f (Hình 8a). Có nhận xét gì về vị trí tương đối của ba điểm A’, B’, C’?
b) Cho hai đường thẳng song song d1 và d2, lấy hai đoạn thẳng bằng nhau AB và DC lần lượt trên d1 và d2. Gọi \({d_1}',{d_2}'\) lần lượt là ảnh của d1, d2 và A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua f (Hình 8b). Tứ giác A’B’C’D’ là hình gì? Nêu nhận xét về vị trí tương đối của hai đường thẳng \({d_1}',{d_2}'\).
c) Cho A’B’C’ là ảnh của tam giác ABC qua f (Hình 8c).
So sánh và \(\Delta ABC\). So sánh số đo hai góc \(\widehat {BAC}\) và \(\widehat {B'A'C'}\).
Phương pháp giải:
Quan sát hình 8 để trả lời
Lời giải chi tiết:
Phép dời hình f bảo toàn khoảng cách giữa hai điểm bất kì.
a) Ta có A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.
Suy ra A’B’ = AB; B’C’ = BC và A’C’ = AC.
Theo đề, ta có ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C).
Suy ra AB + BC = AC.
Khi đó A’B’ + B’C’ = A’C’.
Vậy ba điểm A’, B’, C’ thẳng hàng theo thứ tự (B’ nằm giữa A’ và C’).
b) Ta có AB = DC (giả thiết) và AB // DC (do d1 // d2).
Suy ra tứ giác ABCD là hình bình hành.
Khi đó AD = BC.
Ta có A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua phép dời hình f.
Suy ra A’B’ = AB; D’C’ = DC.
Mà AB = DC (giả thiết), do đó A’B’ = D’C’ (1)
Chứng minh tương tự, ta được A’D’ = B’C’ (2)
Từ (1), (2), suy ra tứ giác A’B’C’D’ là hình bình hành.
Khi đó A’B’ // D’C’ hay \({d_1}'{\rm{//}}{d_2}'\).
Vậy tứ giác A’B’C’D’ là hình bình hành và \({d_1}'{\rm{//}}{d_2}'\).
c) Ta có tam giác A’B’C’ là ảnh của tam giác ABC qua phép dời hình f.
Suy ra A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.
Vì vậy A’B’ = AB; B’C’ = BC và A’C’ = AC.
Do đó ∆A’B’C’ = ∆ABC (c.c.c).
Từ đó suy ra \(\widehat {B'A'C'} = \widehat {BAC}\) (cặp cạnh tương ứng).
Vậy \(\Delta A'B'C'{\rm{ }} = {\rm{ }}\Delta ABC\) và \(\widehat {B'A'C'} = \widehat {BAC}\).
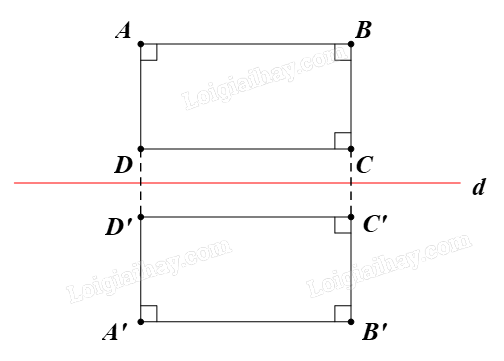
Gọi A’B’C’D’ là ảnh của hình chữ nhật ABCD qua phép biến hình được diễn tả trong Vận dụng. Hãy cho biết A’B’C’D’ là hình gì. Giải thích.
Phương pháp giải:
Phép dời hình bảo toàn:
- Tính thẳng hàng của 3 điểm và thứ tự của ba điểm thẳng hàng.
- Tính song song của hai đường thẳng.
- Độ lớn của một góc.
Lời giải chi tiết:
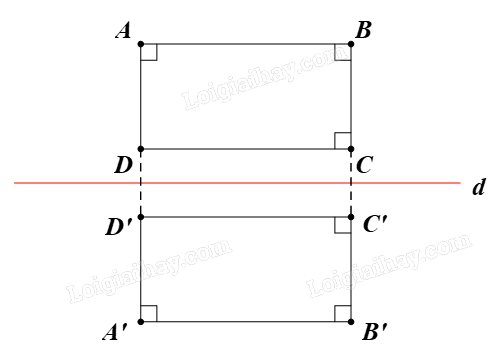
Gọi f là phép biến hình trong Vận dụng.
Trong Vận dụng, ta đã chứng minh được f là một phép dời hình.
Ta có ABCD là hình chữ nhật.
Suy ra \(\;\widehat {DAB} = 90^\circ ;\,\,\widehat {ABC} = 90^\circ ;\,\,\widehat {BCD} = 90^\circ \)
Do phép dời hình f bảo toàn độ lớn của góc nên ta có \(\widehat {{\rm{D'A'B'}}} = 90^\circ ;\widehat {{\rm{A'B'C'}}} = 90^\circ ;\widehat {{\rm{B'C'D'}}} = 90^\circ \)
Vậy A’B’C’D’ cũng là hình chữ nhật.
Giải Mục 3 Trang 8, 9, 10 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 3 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững kiến thức nền tảng và kỹ năng giải quyết vấn đề. Việc hiểu rõ bản chất của từng bài tập là yếu tố then chốt để đạt kết quả tốt. Tusach.vn sẽ cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong Mục 3 trang 8, 9, 10, giúp các em tự tin hơn trong quá trình học tập.
Nội dung chính của Mục 3 (tùy thuộc vào chương cụ thể)
Để hiểu rõ hơn về Mục 3, chúng ta cần xác định nội dung chính mà nó đề cập đến. Thông thường, Mục 3 có thể bao gồm các chủ đề sau:
- Đại số: Giải phương trình, bất phương trình, hệ phương trình, hàm số, đồ thị hàm số.
- Hình học: Đường thẳng, đường tròn, elip, hypebol, parabol, vectơ, tích vô hướng, tích có hướng.
- Lượng giác: Các hàm lượng giác, phương trình lượng giác, tam giác, đường tròn lượng giác.
- Phân tích: Giới hạn, đạo hàm, tích phân, ứng dụng của đạo hàm và tích phân.
Giải chi tiết các bài tập trang 8
Chúng ta sẽ bắt đầu với việc giải chi tiết các bài tập trang 8. Mỗi bài tập sẽ được phân tích kỹ lưỡng, từ việc xác định yêu cầu của đề bài đến việc lựa chọn phương pháp giải phù hợp. Lời giải sẽ được trình bày một cách rõ ràng, dễ hiểu, kèm theo các chú thích và giải thích cần thiết.
Ví dụ (giả định bài tập 1 trang 8):
Bài 1: Giải phương trình 2x + 3 = 7
Lời giải:
- Chuyển 3 sang vế phải: 2x = 7 - 3
- Rút gọn: 2x = 4
- Chia cả hai vế cho 2: x = 2
- Vậy nghiệm của phương trình là x = 2.
Giải chi tiết các bài tập trang 9
Tương tự như trang 8, chúng ta sẽ giải chi tiết các bài tập trang 9. Các bài tập trên trang 9 có thể có độ khó cao hơn, đòi hỏi học sinh phải vận dụng nhiều kiến thức và kỹ năng hơn. Tusach.vn sẽ cung cấp các lời giải chi tiết, kèm theo các mẹo và thủ thuật để giúp các em giải quyết các bài tập một cách hiệu quả.
Giải chi tiết các bài tập trang 10
Cuối cùng, chúng ta sẽ giải chi tiết các bài tập trang 10. Các bài tập trên trang 10 thường là các bài tập tổng hợp, đòi hỏi học sinh phải kết hợp kiến thức từ nhiều chủ đề khác nhau. Tusach.vn sẽ cung cấp các lời giải chi tiết, giúp các em củng cố kiến thức và rèn luyện kỹ năng giải quyết vấn đề.
Mẹo học tập hiệu quả
Để học tập hiệu quả môn Toán 11, các em cần:
- Nắm vững kiến thức nền tảng.
- Luyện tập thường xuyên.
- Tìm hiểu các phương pháp giải bài tập khác nhau.
- Hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn.
- Sử dụng các tài liệu tham khảo, ví dụ như tusach.vn.
Kết luận
Hy vọng rằng, với lời giải chi tiết và hướng dẫn cụ thể của Tusach.vn, các em học sinh sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt trong môn Toán 11. Chúc các em học tập tốt!
| Bài tập | Trang | Lời giải |
|---|---|---|
| Bài 1 | 8 | Xem chi tiết ở trên |
| Bài 2 | 9 | Đang cập nhật |