Giải mục 1 trang 38, 39 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 38, 39 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 38, 39 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp tốt nhất để giúp các bạn học tập hiệu quả.
Bài giải này được xây dựng dựa trên chương trình học chính thức và được kiểm tra kỹ lưỡng để đảm bảo tính chính xác.
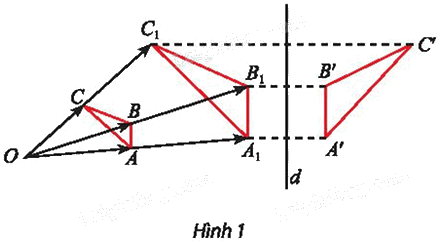
Trong Hình 1, tìm hai phép biến hình để biến tam giác ABC thành tam giác A’B’C’.
Thực hành 1
Cho trước ba số thực a, b, k. Trong mặt phẳng tọa độ Oxy, xét phép biến hình g biến điểm M(x; y) thành điểm M’(x’; y’) thỏa mãn: \(\left\{ \begin{array}{l}x' = kx + a\\y' = ky + b\end{array} \right.\) . Hãy chứng minh g là một phép đồng dạng.
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
Xét hai điểm bất kì \(M({x_1};{\rm{ }}{y_1}),{\rm{ }}N({x_2};{\rm{ }}{y_2})\) có ảnh qua g lần lượt là
Ta có \(\overrightarrow {MN} = \left( {{x_2} - {x_1};{y_2} - {y_1}} \right)\)
Và \(\overrightarrow {M'N'} = \left( {k{x_2} + a - k{x_1} - a;k{y_2} + b - k{y_1} - b} \right)\) \( = \left( {k\left( {{x_2} - {x_1}} \right);k\left( {{y_2} - {y_1}} \right)} \right)\)
Do đó \(\overrightarrow {M'N'} = k\left( {{x_2} - {x_1};{y_2} - {y_1}} \right)\)
Vì vậy \(\overrightarrow {M'N'} = k\overrightarrow {MN} \)
Suy ra \(M'N'{\rm{ }} = {\rm{ }}\left| k \right|.MN.\)
Vậy g là phép đồng dạng tỉ số \(\left| k \right|\).
Khám phá 1
Trong Hình 1, tìm hai phép biến hình để biến tam giác ABC thành tam giác A’B’C’.
Phương pháp giải:
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết:
Để tìm phép biến hình biến \(\Delta \)ABC thành \(\Delta \)A’B’C’, ta tìm phép biến hình biến ∆ABC thành \(\Delta \)\({A_1}{B_1}{C_1}\;\) và tìm phép biến hình biến \(\Delta \)\({A_1}{B_1}{C_1}\;\) thành \(\Delta \)A’B’C’.
⦁ Để tìm phép biến hình biến \(\Delta \)ABC thành \(\Delta \)A1B1C1, ta tìm phép biến hình biến các điểm A, B, C theo thứ tự thành các điểm \({A_1},{\rm{ }}{B_1},{\rm{ }}{C_1}.\)
Ta thấy các đường thẳng \(A{A_1},{\rm{ }}B{B_1},{\rm{ }}C{C_1}\;\) đồng quy tại O.
Xét phép vị tự tâm O, tỉ số k biến các điểm A, B, C theo thứ tự thành các điểm A1, B1, C1.
Ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right){\rm{ }} = {\rm{ }}{A_1}.\)
Suy ra \(\overrightarrow {O{A_1}} = k\overrightarrow {OA} \) và \(O{A_1}\; = {\rm{ }}\left| k \right|.OA.\)
Vì A, A1 nằm cùng phía đối với O nên k > 0.
Do đó \(k = \frac{{O{A_1}}}{{OA}}\).
Tương tự ta cũng có \(k = \frac{{O{B_1}}}{{OB}},k = \frac{{O{C_1}}}{{OC}}\)
Do đó \(k = \frac{{O{A_1}}}{{OA}} = \frac{{O{B_1}}}{{OB}} = \frac{{O{C_1}}}{{OC}}\)
Vì vậy \({V_{\left( {O;\frac{{O{A_1}}}{{OA}}} \right)}}\) là phép biến hình biến \(\Delta \)ABC thành \(\Delta {A_1}{B_1}{C_1}.\)
⦁ Để tìm phép biến hình biến \(\Delta {A_1}{B_1}{C_1}.\) thành \(\Delta \)A’B’C’, ta tìm phép biến hình biến các điểm A1, B1, C1 theo thứ tự thành các điểm A’, B’, C’.
Ta thấy d là đường trung trực của đoạn A1A’.
Suy ra \({D_d}({A_1}){\rm{ }} = {\rm{ }}A'.\)
Chứng minh tương tự, ta được \({D_d}({B_1}){\rm{ }} = {\rm{ }}B';{\rm{ }}{D_d}({C_1}){\rm{ }} = {\rm{ }}C'.\)
Vì vậy Đd là phép biến hình biến \(\Delta \)A1B1C1 thành \(\Delta \)A’B’C’.
Vậy hai phép biến hình biến tam giác ABC thành tam giác A’B’C’ là \({V_{\left( {O;\frac{{O{A_1}}}{{OA}}} \right)}}\) biến \(\Delta \)ABC thành \(\Delta \)A1B1C1 và \({D_d}\) biến \(\Delta \)A1B1C1 thành \(\Delta \)A’B’C’.
Vận dụng 1
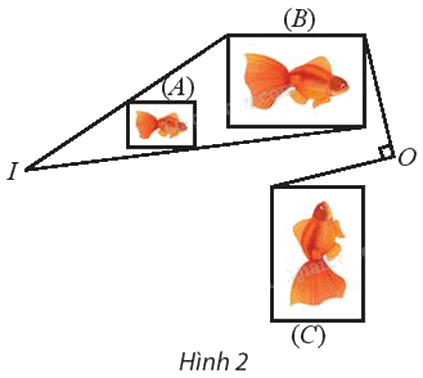
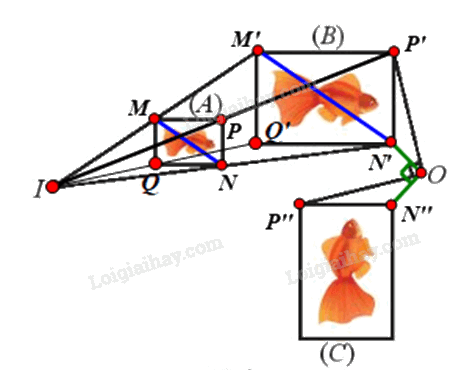
Tìm phép đồng dạng biến hình (A) thành hình (C).
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
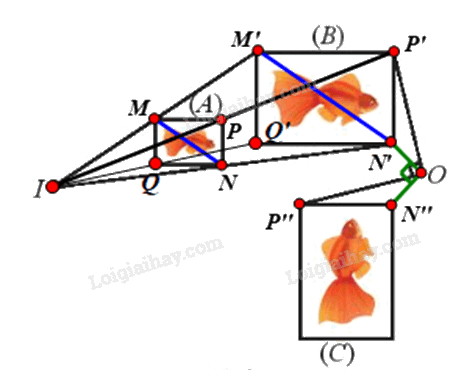
Gọi f là phép đồng dạng cần tìm.
⦁ Để tìm phép biến hình biến hình (A) thành hình (B), ta tìm phép biến hình biến các điểm M, N, P, Q theo thứ tự thành các điểm M’, N’, P’, Q’.
Ta thấy các đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại I.
Xét phép vị tự tâm I, tỉ số k biến các điểm M, N, P, Q theo thứ tự thành các điểm M’, N’, P’, Q’.
Ta có \({V_{(I,{\rm{ }}k)}}\left( M \right){\rm{ }} = {\rm{ }}M'.\)
Suy ra và
Vì M, M’ nằm cùng phía đối với I nên \(k{\rm{ }} > {\rm{ }}0.\)
Do đó \(k = \frac{{OM'}}{{OM}}.\)
Tương tự ta cũng có \(k = \frac{{ON'}}{{ON}},k = \frac{{OP'}}{{OP}},k = \frac{{OQ'}}{{OQ}}\)
Do đó \(k = \frac{{OM'}}{{OM}} = \frac{{ON'}}{{ON}} = \frac{{OP'}}{{OP}} = \frac{{OQ'}}{{OQ}}\)
Vì vậy \({V_{\left( {I;\frac{{OM'}}{{OM}}} \right)}}\) là phép biến hình biến hình (A) thành hình (B).
⦁ Ta thấy OP’ = OP” và \(\widehat {P'OP''} = {90^o}\)
Suy ra phép quay tâm O, góc quay 90° biến điểm P’ thành điểm P”.
Chứng minh tương tự, ta thấy \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\;\) cũng biến các điểm khác trên hình (B) thành các điểm có vị trí tương ứng trên hình (C).
Vì vậy \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\;\) biến hình (B) thành hình (C).
⦁ Xét hai điểm N, P, ta có:
+) \(N' = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( N \right){\rm{, }}N''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {N'} \right);\)
+) \(P'{\rm{ }} = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( P \right),P''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {P'} \right).\)
Do đó:
+) \(N'P'{\rm{ }} = {\rm{ }}{V_{(I,{\rm{ }}k)}}\left( {NP} \right)\). Suy ra \(N'P'{\rm{ }} = {\rm{ }}k.NP;\)
+) \(N''P''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {N'P'} \right).\)Suy ra \(N''P''{\rm{ }} = {\rm{ }}N'P'.\)
Vì vậy \(N''P'' = {\rm{ }}N'P'{\rm{ }} = {\rm{ }}k.NP.\)
Vậy f là phép đồng dạng tỉ số k \(\left( {k{\rm{ }} > {\rm{ }}0} \right)\) biến (A) thành (C) thỏa mãn \(\left( B \right){\rm{ }} = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( {\left( A \right)} \right)\) và \(\left( C \right){\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {\left( B \right)} \right);\)
- Khám phá 1
- Thực hành 1
- Vận dụng 1
Trong Hình 1, tìm hai phép biến hình để biến tam giác ABC thành tam giác A’B’C’.
Phương pháp giải:
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết:
Để tìm phép biến hình biến \(\Delta \)ABC thành \(\Delta \)A’B’C’, ta tìm phép biến hình biến ∆ABC thành \(\Delta \)\({A_1}{B_1}{C_1}\;\) và tìm phép biến hình biến \(\Delta \)\({A_1}{B_1}{C_1}\;\) thành \(\Delta \)A’B’C’.
⦁ Để tìm phép biến hình biến \(\Delta \)ABC thành \(\Delta \)A1B1C1, ta tìm phép biến hình biến các điểm A, B, C theo thứ tự thành các điểm \({A_1},{\rm{ }}{B_1},{\rm{ }}{C_1}.\)
Ta thấy các đường thẳng \(A{A_1},{\rm{ }}B{B_1},{\rm{ }}C{C_1}\;\) đồng quy tại O.
Xét phép vị tự tâm O, tỉ số k biến các điểm A, B, C theo thứ tự thành các điểm A1, B1, C1.
Ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right){\rm{ }} = {\rm{ }}{A_1}.\)
Suy ra \(\overrightarrow {O{A_1}} = k\overrightarrow {OA} \) và \(O{A_1}\; = {\rm{ }}\left| k \right|.OA.\)
Vì A, A1 nằm cùng phía đối với O nên k > 0.
Do đó \(k = \frac{{O{A_1}}}{{OA}}\).
Tương tự ta cũng có \(k = \frac{{O{B_1}}}{{OB}},k = \frac{{O{C_1}}}{{OC}}\)
Do đó \(k = \frac{{O{A_1}}}{{OA}} = \frac{{O{B_1}}}{{OB}} = \frac{{O{C_1}}}{{OC}}\)
Vì vậy \({V_{\left( {O;\frac{{O{A_1}}}{{OA}}} \right)}}\) là phép biến hình biến \(\Delta \)ABC thành \(\Delta {A_1}{B_1}{C_1}.\)
⦁ Để tìm phép biến hình biến \(\Delta {A_1}{B_1}{C_1}.\) thành \(\Delta \)A’B’C’, ta tìm phép biến hình biến các điểm A1, B1, C1 theo thứ tự thành các điểm A’, B’, C’.
Ta thấy d là đường trung trực của đoạn A1A’.
Suy ra \({D_d}({A_1}){\rm{ }} = {\rm{ }}A'.\)
Chứng minh tương tự, ta được \({D_d}({B_1}){\rm{ }} = {\rm{ }}B';{\rm{ }}{D_d}({C_1}){\rm{ }} = {\rm{ }}C'.\)
Vì vậy Đd là phép biến hình biến \(\Delta \)A1B1C1 thành \(\Delta \)A’B’C’.
Vậy hai phép biến hình biến tam giác ABC thành tam giác A’B’C’ là \({V_{\left( {O;\frac{{O{A_1}}}{{OA}}} \right)}}\) biến \(\Delta \)ABC thành \(\Delta \)A1B1C1 và \({D_d}\) biến \(\Delta \)A1B1C1 thành \(\Delta \)A’B’C’.
Cho trước ba số thực a, b, k. Trong mặt phẳng tọa độ Oxy, xét phép biến hình g biến điểm M(x; y) thành điểm M’(x’; y’) thỏa mãn: \(\left\{ \begin{array}{l}x' = kx + a\\y' = ky + b\end{array} \right.\) . Hãy chứng minh g là một phép đồng dạng.
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
Xét hai điểm bất kì \(M({x_1};{\rm{ }}{y_1}),{\rm{ }}N({x_2};{\rm{ }}{y_2})\) có ảnh qua g lần lượt là
Ta có \(\overrightarrow {MN} = \left( {{x_2} - {x_1};{y_2} - {y_1}} \right)\)
Và \(\overrightarrow {M'N'} = \left( {k{x_2} + a - k{x_1} - a;k{y_2} + b - k{y_1} - b} \right)\) \( = \left( {k\left( {{x_2} - {x_1}} \right);k\left( {{y_2} - {y_1}} \right)} \right)\)
Do đó \(\overrightarrow {M'N'} = k\left( {{x_2} - {x_1};{y_2} - {y_1}} \right)\)
Vì vậy \(\overrightarrow {M'N'} = k\overrightarrow {MN} \)
Suy ra \(M'N'{\rm{ }} = {\rm{ }}\left| k \right|.MN.\)
Vậy g là phép đồng dạng tỉ số \(\left| k \right|\).
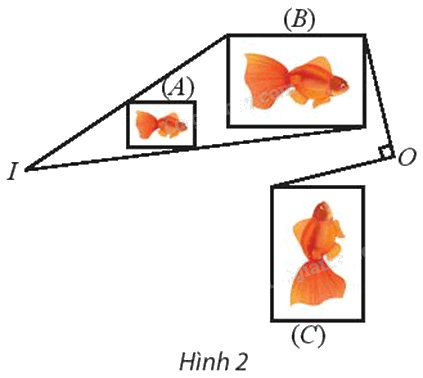
Tìm phép đồng dạng biến hình (A) thành hình (C).
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
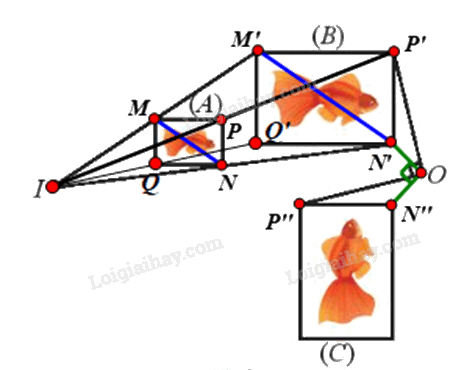
Gọi f là phép đồng dạng cần tìm.
⦁ Để tìm phép biến hình biến hình (A) thành hình (B), ta tìm phép biến hình biến các điểm M, N, P, Q theo thứ tự thành các điểm M’, N’, P’, Q’.
Ta thấy các đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại I.
Xét phép vị tự tâm I, tỉ số k biến các điểm M, N, P, Q theo thứ tự thành các điểm M’, N’, P’, Q’.
Ta có \({V_{(I,{\rm{ }}k)}}\left( M \right){\rm{ }} = {\rm{ }}M'.\)
Suy ra và
Vì M, M’ nằm cùng phía đối với I nên \(k{\rm{ }} > {\rm{ }}0.\)
Do đó \(k = \frac{{OM'}}{{OM}}.\)
Tương tự ta cũng có \(k = \frac{{ON'}}{{ON}},k = \frac{{OP'}}{{OP}},k = \frac{{OQ'}}{{OQ}}\)
Do đó \(k = \frac{{OM'}}{{OM}} = \frac{{ON'}}{{ON}} = \frac{{OP'}}{{OP}} = \frac{{OQ'}}{{OQ}}\)
Vì vậy \({V_{\left( {I;\frac{{OM'}}{{OM}}} \right)}}\) là phép biến hình biến hình (A) thành hình (B).
⦁ Ta thấy OP’ = OP” và \(\widehat {P'OP''} = {90^o}\)
Suy ra phép quay tâm O, góc quay 90° biến điểm P’ thành điểm P”.
Chứng minh tương tự, ta thấy \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\;\) cũng biến các điểm khác trên hình (B) thành các điểm có vị trí tương ứng trên hình (C).
Vì vậy \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\;\) biến hình (B) thành hình (C).
⦁ Xét hai điểm N, P, ta có:
+) \(N' = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( N \right){\rm{, }}N''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {N'} \right);\)
+) \(P'{\rm{ }} = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( P \right),P''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {P'} \right).\)
Do đó:
+) \(N'P'{\rm{ }} = {\rm{ }}{V_{(I,{\rm{ }}k)}}\left( {NP} \right)\). Suy ra \(N'P'{\rm{ }} = {\rm{ }}k.NP;\)
+) \(N''P''{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {N'P'} \right).\)Suy ra \(N''P''{\rm{ }} = {\rm{ }}N'P'.\)
Vì vậy \(N''P'' = {\rm{ }}N'P'{\rm{ }} = {\rm{ }}k.NP.\)
Vậy f là phép đồng dạng tỉ số k \(\left( {k{\rm{ }} > {\rm{ }}0} \right)\) biến (A) thành (C) thỏa mãn \(\left( B \right){\rm{ }} = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( {\left( A \right)} \right)\) và \(\left( C \right){\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {\left( B \right)} \right);\)
Giải mục 1 trang 38, 39 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Mục 1 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về đạo hàm. Đây là một phần quan trọng trong chương trình Toán 11, đóng vai trò nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Việc nắm vững các khái niệm và kỹ năng liên quan đến đạo hàm là điều cần thiết để giải quyết các bài toán phức tạp và đạt kết quả tốt trong các kỳ thi.
Nội dung chính của Mục 1
- Ôn tập về đạo hàm: Nhắc lại các định nghĩa, tính chất và quy tắc tính đạo hàm của các hàm số cơ bản.
- Đạo hàm của hàm hợp: Hướng dẫn cách tính đạo hàm của hàm hợp bằng quy tắc chuỗi.
- Đạo hàm của hàm ẩn: Giới thiệu phương pháp tìm đạo hàm của hàm ẩn.
- Ứng dụng của đạo hàm: Sử dụng đạo hàm để giải các bài toán liên quan đến cực trị, khoảng đơn điệu và vẽ đồ thị hàm số.
Giải chi tiết các bài tập trang 38, 39
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 38, 39 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo:
Bài 1: Tính đạo hàm của các hàm số sau:
- f(x) = 3x2 + 2x - 1
- g(x) = sin(x) + cos(x)
- h(x) = ex + ln(x)
Giải:
- f'(x) = 6x + 2
- g'(x) = cos(x) - sin(x)
- h'(x) = ex + 1/x
Bài 2: Cho hàm số y = x3 - 3x2 + 2x. Tìm các điểm cực trị của hàm số.
Giải:
y' = 3x2 - 6x + 2
Giải phương trình y' = 0, ta được x1 = (3 + √3)/3 và x2 = (3 - √3)/3
Tính y'' = 6x - 6
y''(x1) = 6((3 + √3)/3) - 6 = 2√3 > 0, suy ra hàm số đạt cực tiểu tại x1
y''(x2) = 6((3 - √3)/3) - 6 = -2√3 < 0, suy ra hàm số đạt cực đại tại x2
Bài 3: Tìm khoảng đơn điệu của hàm số y = x4 - 4x2 + 3.
Giải:
y' = 4x3 - 8x = 4x(x2 - 2)
Giải phương trình y' = 0, ta được x = 0, x = √2, x = -√2
Xét dấu y' trên các khoảng (-∞, -√2), (-√2, 0), (0, √2), (√2, +∞), ta xác định được khoảng đồng biến và nghịch biến của hàm số.
Lời khuyên khi học tập
Để học tốt môn Toán 11, đặc biệt là phần đạo hàm, bạn nên:
- Nắm vững các định nghĩa, tính chất và quy tắc tính đạo hàm.
- Luyện tập thường xuyên các bài tập từ cơ bản đến nâng cao.
- Sử dụng các tài liệu tham khảo, sách bài tập và các trang web học trực tuyến để bổ sung kiến thức.
- Hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn.
Tusach.vn hy vọng rằng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về Mục 1 trang 38, 39 Chuyên đề học tập Toán 11 - Chân trời sáng tạo và đạt kết quả tốt trong học tập. Chúc các bạn thành công!