Giải khởi động trang 6 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tổng quan nội dung
Giải khởi động trang 6 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Bài Giải khởi động trang 6 Chuyên đề học tập Toán 11 - Chân trời sáng tạo là phần mở đầu quan trọng, giúp học sinh ôn lại kiến thức cũ và làm quen với nội dung mới của chuyên đề.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh tự học hiệu quả và nắm vững kiến thức.
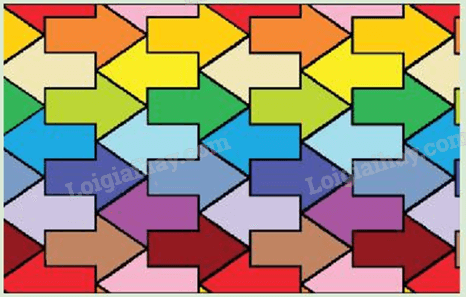
: Bức tranh trang trí trong hình bên trước khi tô màu thực chất được tạo ra từ một hình mũi tên duy nhất và được dời chỗ tới các vị trí khác nhau.
Đề bài
Bức tranh trang trí trong hình bên trước khi tô màu thực chất được tạo ra từ một hình mũi tên duy nhất và được dời chỗ tới các vị trí khác nhau. Hãy thảo luận để tìm hiểu về các phép biến đổi hình học nào đã tạo ra tất cả các hình mũi tên như vậy từ một hình mũi tên ban đầu.
Phương pháp giải - Xem chi tiết
Quan sát hình vẽ để trả lời
Lời giải chi tiết
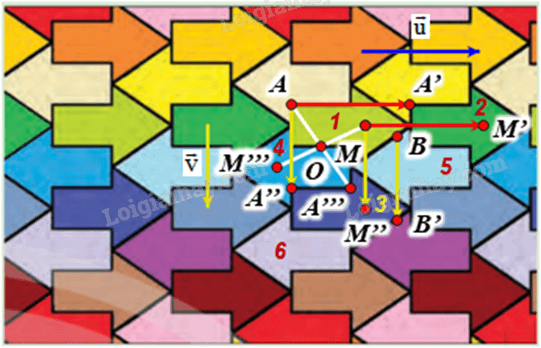
Giả sử mũi tên ban đầu là mũi tên đánh số 1.
+ Gọi A là một điểm trên hình mũi tên 1 và \(\vec u\) có phương song song với trục đối xứng của hình mũi tên 1, độ dài của \(\vec u\) bằng độ dài từ điểm đầu tới điểm cuối của mũi tên 1 (hình vẽ).
Lấy điểm A’ sao cho \(\overrightarrow {AA'} = \vec u\)
Khi đó điểm A’ là một điểm trên hình mũi tên 2 có vị trí tương ứng với điểm A trên hình mũi tên 1.
Tương tự, với mỗi điểm M bất kì trên hình mũi tên 1, ta lấy điểm M’ sao cho \(\overrightarrow {MM'} = \vec u\) thì từ hình mũi tên 1 là tập hợp điểm M, ta được tập hợp các điểm M’ tạo thành hình mũi tên 2.
+ Gọi A’’ là một điểm trên hình mũi tên 3 có vị trí tương ứng với điểm A trên hình mũi tên 1.
Giả sử \(\vec v\) là vectơ có phương vuông góc với trục đối xứng của hình mũi tên 1, độ dài bằng độ dài từ điểm A đến điểm A’’ (hình vẽ).
Tức là, \(\vec v = \overrightarrow {AA''} \).
Gọi B là một điểm trên hình mũi tên 1.
Lấy điểm B’ sao cho \(\overrightarrow {BB'} = \vec v\).
Khi đó điểm B’ là một điểm trên hình mũi tên 3 có vị trí tương ứng với điểm B trên hình mũi tên 1.
Tương tự, với mỗi điểm M bất kì trên hình mũi tên 1, ta lấy điểm M’’ sao cho \(\overrightarrow {MM''} = \vec v\) thì từ hình mũi tên 1 là tập hợp điểm M, ta được tập hợp các điểm M’’ tạo thành hình mũi tên 3.
+ Gọi O là một điểm trên hình mũi tên 1 (hình vẽ).
Lấy điểm A’’’ đối xứng với A qua O.
Khi đó điểm A’’’ là một điểm trên hình mũi tên 4 có vị trí tương ứng với điểm A trên hình mũi tên 1.
Tương tự, với mỗi điểm M bất kì trên hình mũi tên 1, ta lấy điểm M’’’ đối xứng với M qua O thì từ hình mũi tên 1 là tập hợp điểm M, ta được tập hợp các điểm M’’’ tạo thành hình mũi tên 4.
+ Tương tự trường hợp chứng minh từ hình mũi tên 1 thành hình mũi tên 2, ta chứng minh được trường hợp từ hình mũi tên 4 thành hình mũi tên 5.
+ Tương tự trường hợp chứng minh từ hình mũi tên 1 thành hình mũi tên 3, ta chứng minh được trường hợp từ hình mũi tên 4 thành hình mũi tên 6.
+ Tương tự như vậy với tất cả các hình mũi tên khác.
Vậy hai phép biến đổi hình học cần tìm là phép biến đổi theo vectơ \(\vec u\) có phương song song với trục đối xứng, độ dài bằng độ dài từ điểm đầu tới điểm cuối của mũi tên ban đầu và phép biến đổi lấy điểm đối xứng qua một điểm.
Giải khởi động trang 6 Chuyên đề học tập Toán 11 - Chân trời sáng tạo: Tổng quan và Hướng dẫn Giải Chi Tiết
Bài Giải khởi động trang 6 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo đóng vai trò quan trọng trong việc giúp học sinh làm quen với các khái niệm và kỹ năng mới sẽ được trình bày trong chuyên đề. Đây là cơ hội để ôn lại kiến thức nền tảng, kết nối kiến thức cũ với kiến thức mới, và chuẩn bị tâm lý cho việc học tập chuyên sâu hơn.
Mục tiêu của Bài Giải khởi động
- Ôn tập kiến thức cũ: Bài tập thường tập trung vào việc nhắc lại các kiến thức đã học ở các lớp trước, đặc biệt là các kiến thức liên quan đến đại số, hình học và giải tích.
- Giới thiệu kiến thức mới: Bài tập có thể chứa đựng những gợi ý, manh mối về nội dung mới sẽ được học trong chuyên đề.
- Phát triển tư duy: Bài tập khuyến khích học sinh suy nghĩ, phân tích và vận dụng kiến thức để giải quyết vấn đề.
Nội dung Bài Giải khởi động trang 6
Nội dung cụ thể của bài tập khởi động trang 6 sẽ khác nhau tùy thuộc vào từng chuyên đề. Tuy nhiên, thường sẽ bao gồm các dạng bài tập sau:
- Bài tập trắc nghiệm: Kiểm tra kiến thức cơ bản và khả năng nhận biết các khái niệm.
- Bài tập tự luận: Yêu cầu học sinh trình bày lời giải chi tiết, thể hiện khả năng vận dụng kiến thức và kỹ năng.
- Bài tập ứng dụng: Liên hệ kiến thức toán học với thực tế, giúp học sinh hiểu rõ hơn về ý nghĩa và tầm quan trọng của toán học.
Hướng dẫn Giải chi tiết tại Tusach.vn
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo, bao gồm cả bài Giải khởi động trang 6. Lời giải của chúng tôi được xây dựng bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và khoa học.
Các bước giải bài tập thường được trình bày rõ ràng:
- Phân tích đề bài: Xác định yêu cầu của đề bài, các dữ kiện đã cho và các kiến thức cần sử dụng.
- Lập kế hoạch giải: Xác định các bước cần thực hiện để giải quyết bài toán.
- Thực hiện giải: Thực hiện các bước giải theo kế hoạch đã lập.
- Kiểm tra lại kết quả: Đảm bảo kết quả thu được là chính xác và phù hợp với yêu cầu của đề bài.
Ví dụ minh họa (Giả định nội dung bài tập)
Bài tập: Tính giá trị của biểu thức A = (x + 2)(x - 2) khi x = 3.
Lời giải:
A = (x + 2)(x - 2) = x2 - 4
Thay x = 3 vào biểu thức, ta được:
A = 32 - 4 = 9 - 4 = 5
Vậy, giá trị của biểu thức A khi x = 3 là 5.
Lợi ích khi sử dụng Tusach.vn
- Tiết kiệm thời gian: Lời giải chi tiết giúp học sinh nhanh chóng nắm bắt kiến thức và giải quyết bài tập.
- Nâng cao hiệu quả học tập: Lời giải dễ hiểu giúp học sinh hiểu sâu sắc kiến thức và phát triển tư duy.
- Chuẩn bị tốt cho kỳ thi: Lời giải chính xác giúp học sinh tự tin làm bài thi và đạt kết quả cao.
Lời khuyên khi học tập
Để học tập hiệu quả, các em học sinh nên:
- Đọc kỹ đề bài: Hiểu rõ yêu cầu của đề bài trước khi bắt đầu giải.
- Ôn tập kiến thức cũ: Đảm bảo nắm vững kiến thức nền tảng trước khi học kiến thức mới.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và củng cố kiến thức.
- Hỏi thầy cô giáo: Nếu gặp khó khăn, hãy hỏi thầy cô giáo để được hướng dẫn và giải đáp.
Tusach.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục tri thức. Chúc các em học tập tốt!